В первой статье цикла мы разбирались, что означает “подогнать линию” (или “линейная регрессия”). Мы объяснили интуитивный подход, лежащий в основе алгоритма, и результат, которого хотим добиться, подгоняя линию к данным.
Мы пришли к выводу, что “подогнать линию” означает получить линию, которая располагается как можно ближе к точкам данных.
Нужно ли, чтобы эта линия была максимально близка к каждой точке, и возможно ли это вообще? Ответим на эти вопросы чуть ниже.
Мы также говорили о том, что такая линия может быть выражена следующим уравнением для нашей задачи (прогнозирование цен на жилье):
p^= mr + b,
где p^ — прогнозируемая цена, m — цена за комнату, r — количество комнат, b — базовая цена дома.
Мы назвали кратную величину цены за комнату (m) “весом” признака количества комнат (r), а базовую цену дома — “смещением” в уравнении.
Мы видели, что при корректировке веса и смещения в уравнении даже на небольшую величину предсказанный результат становится ближе к фактической точке данных.
В этой статье мы постараемся ответить на следующие вопросы.
- Какие способы можно применить для нахождения нужных весов и смещения?
- Как эти способы помогут алгоритму понять, насколько нужно изменить веса и смещение и в каком направлении?
- Какой именно путь из множества вариантов следует выбрать?
В целом, мы будем разбираться, как настроить веса и смещение.
Как вес и смещение влияют на положение линии
Дадим термину “вес” новое название — “наклон” (на это есть причина).
Теперь вспомним, что вышеприведенное уравнение состоит из двух компонентов:
- наклон;
- y-пересечение (или смещение).
Если мы попробуем нарисовать линию, используя эти две метрики, то получим нечто подобное:
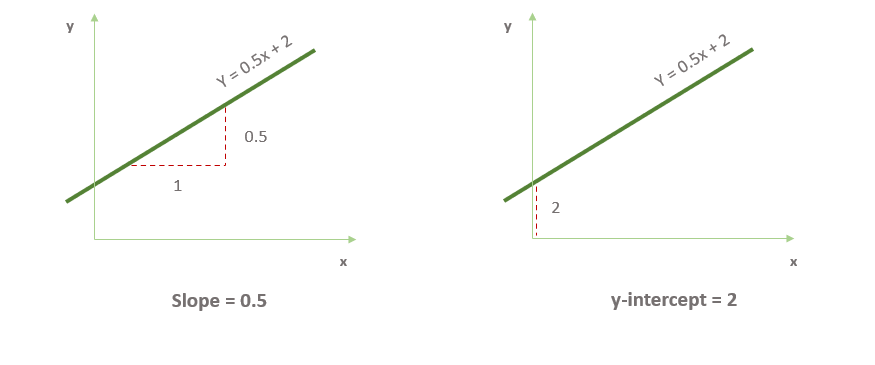
Наклон показывает, насколько крута линия (отсюда и название “наклон”), а y-пересечение — место, где находится линия. Первый определяется как подъем, поделенный на спуск, а второе — как точка пересечения линии с осью y.
Итак, что означает уравнение y = 0,5x + 2?
Если наклон равен 0,5, это означает следующее: когда мы движемся вдоль этой линии, смещаясь вправо на каждую единицу, мы смещаемся на 0,5 единицы вверх. Наклон может быть нулевым, если мы не двигаемся вверх, или отрицательным, если мы двигаемся вниз.
Если провести любую параллельную линию к линии на рисунке выше, то эта линия также будет подниматься на 0,5 единицы на каждую единицу движения вправо.
Именно здесь и вступает в дело y-пересечение. Оно показывает, где линия пересекает ось y. Эта конкретная линия пересекает ось x на высоте 2 — это и есть y-пересечение.
Другими словами, наклон линии говорит о направлении, в котором она указывает, а y-пересечение — о местоположении линии.
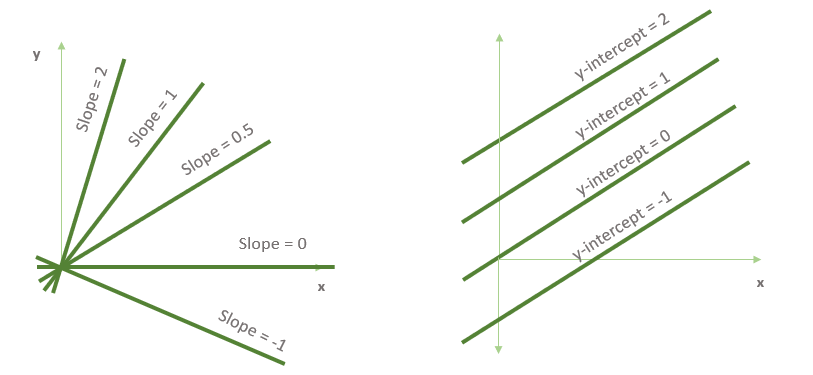
Освежим в памяти нашу задачу по прогнозированию цен на жилье, а также возьмем вышеприведенные сдвиги линий для изменения наклона (цена за комнату) и базовой цены (базовая цена дома).
Если мы добавим еще несколько деталей к сдвигам на рисунке выше, то получится нечто подобное:
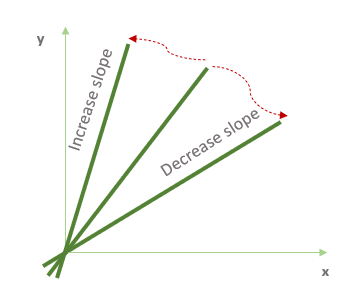
- Если увеличить наклон линии, она будет вращаться против часовой стрелки.
- Если уменьшить наклон линии, то линия будет вращаться по часовой стрелке.
Эти вращения происходят в точке пересечения линии и оси y.
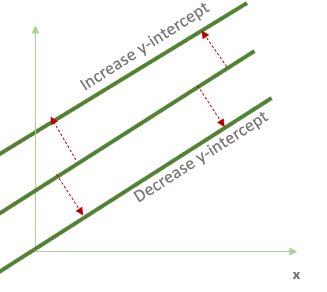
- Если мы увеличим y-пересечение линии, то линия будет перемещена вверх.
- Если мы уменьшим y-пересечение линии, линия будет перемещена вниз.
Теперь, когда у нас есть все “ингредиенты” — наклон, y-пересечение и уравнение линии, — можно переходить к практической части.
Простой способ перемещения линии ближе к множеству точек (к одной из точек за раз)
Способ действительно простой, и это можно понять, посмотрев на рисунок ниже:
Вспомните наше уравнение для прогнозирования цен на жилье. В нем y — это цена дома, а x — количество комнат. Следовательно, каждая точка данных будет определенной координатой (r,p).
Представим, что нужно написать псевдокод для простого способа перемещения. Вот что у нас есть.
Входные данные:
- Линия с наклоном m, y-пересечение b и уравнение p̂=mr+b.
- Точка с координатами (r,p).
Выходные данные:
- Линия с уравнением p̂=m’r+b, которая находится ближе к точке (здесь знак над “m” — это “хеш”).
Как реализовать этот простой способ?
Выберите два очень маленьких случайных числа. Назовите их η1 и η2 (буква “эта” из греческого алфавита).
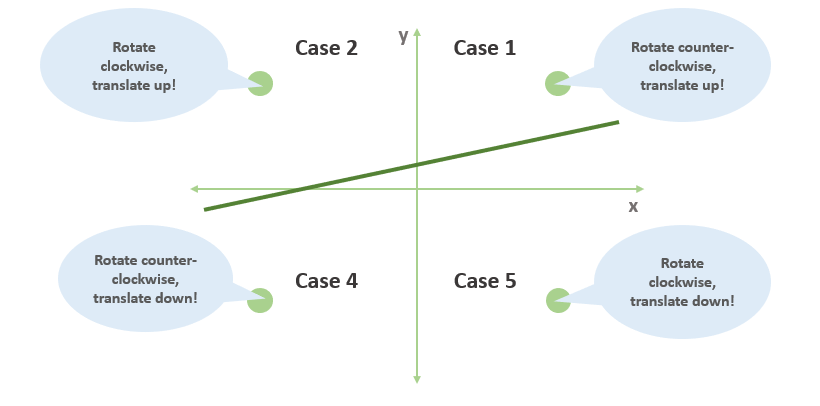
Случай 1. Если точка находится над линией и справа от оси y, поворачиваем линию против часовой стрелки и перемещаем ее вверх.
- Добавьте η1 к наклону m. Получается m’+η1.
- Добавьте η2 к y-пересечению b. Получается b’+η2.
Случай 2. Если точка находится выше линии и слева от оси y, поворачиваем линию по часовой стрелке и перемещаем ее вверх.
- Вычтите η1 из наклона m. Получается m’-η1.
- Прибавьте η2 к y-пересечению b. Получается b’+η2.
Случай 3. Если точка находится ниже линии и справа от оси y, поворачиваем линию по часовой стрелке и перемещаем ее вниз.
- Вычтите η1 из наклона m. Получается m’-η1.
- Вычтите η2 из y-пересечения b. Получается b’-η2.
Случай 4. Если точка находится ниже линии и слева от оси y, поворачиваем линию против часовой стрелки и перемещаем ее вниз.
- Прибавьте η1 к наклону m. Получается m’+η1.
- Вычтите η2 из y-пересечения b. Получается b’-η2.
Результат: линия с уравнением p̂=m’r+b’.
Итак, подведем промежуточные итоги.
- Если модель выдает цену дома, которая намного ниже фактической, добавьте небольшую случайную сумму к цене за комнату и к базовой цене дома.
- Если модель выдает цену дома, которая выше фактической, вычтите небольшое случайное количество из цены за комнату и базовой цены дома.
Но в отношении этого способа возникает несколько вопросов.
- Можно ли выбирать лучшие значения для η1 и η2?
- Можно ли сократить четыре случая до двух или даже одного?
Вот тут-то и пригодится следующий способ!
Квадратичный способ перемещения линии ближе к одной из точек
С помощью квадратичного способа можно свести четыре вышеупомянутых случая к одному, найдя значения с правильными знаками (+ или -), которые нужно добавить к наклону и y-пересечению, чтобы линия всегда двигалась ближе к точке.
Используя простой способ, мы совершаем следующие действия.
- Когда точка находится выше линии, мы прибавляем небольшую величину к y-пересечению. Когда точка находится ниже линии, вычитаем небольшую величину.
- Если точка находится выше линии, значение p-p̂ (разница между ценой и прогнозируемой ценой) положительное. Если точка находится ниже линии, это значение отрицательное.
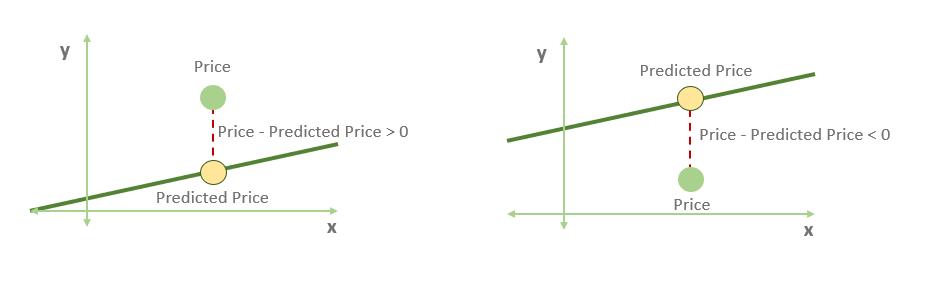
Сложив эти две точки в одну, мы приходим к выводу, что если к y-пересечению добавить разницу p-p̂, то линия всегда будет двигаться к точке. Дело в том, что это значение положительно, когда точка находится над линией, и отрицательно, когда точка находится под ней.
Но в МО следует быть осторожным при внесении корректировок и всегда двигаться не спеша. Введем еще один термин — скорость обучения.
Скорость обучения
Перед обучением модели мы выбираем очень маленькое число. Так мы будем знать, что модель в процессе обучения изменится незначительно.
Обозначим скорость обучения греческой буквой η (“эта”).
Поскольку скорость обучения мала, то и значение η(p-p̂) будет небольшим. Это значение мы прибавляем к y-пересечению, чтобы переместить линию в направлении точки.
Возвращаемся к наклону. Действия будут аналогичны тем, которые мы совершали в отношении y-пересечения, но только немного сложнее.
- Используя простой способ, когда точка находится в положении, описанном в случаях 1 и 4 (над линией и справа от вертикальной оси или под линией и слева от вертикальной оси), мы вращаем линию против часовой стрелки. В других случаях (случаи 2 и 3), мы вращаем ее по часовой стрелке.
- Если точка (r,p) находится справа от вертикальной оси, то значение r положительно. Если точка находится слева от вертикальной оси, оно будет отрицательно. Обратите внимание: в данном примере r никогда не будет отрицательным, так как оно указывает на количество комнат. Однако чисто теоретически признак может быть отрицательным.
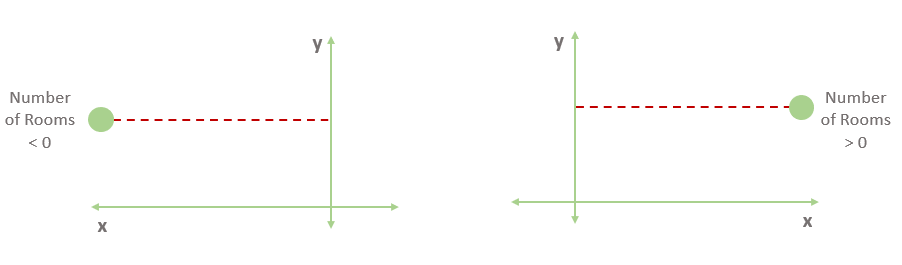
Рассмотрим значение r(p-p̂). Оно положительно, когда r и p-p̂ оба положительны или оба отрицательны. Именно так обстоит дело в сценариях 1 и 4. В случаях 2 и 3 r(p-p̂) отрицательно.
Поскольку это значение должно быть небольшим, то умножаем его на скорость обучения и делаем вывод, что добавление ηr(p-p̂) к наклону всегда будет двигать линию в направлении точки.
Представим, что нужно написать псевдокод для квадратичного способа.
Входные данные:
- Линия с наклоном m, y-пересечение b и уравнение p̂=mr + b.
- Точка с координатами (r,p).
- Небольшое положительное значение η (скорость обучения).
Выходные данные:
- Линия с уравнением p̂ = m’r + b’, которая ближе к точке.
Как реализовать квадратичный способ?
- Добавьте η(p-(p))̂ к y-пересечению b. Получается b’ = b+η(p-(p))̂ (это переместит линию).
- Добавьте ηr(p-(p))̂ к наклону m. Получается m’ = m+ηr(p-(p))̂ (это повернет линию).
Результат: линия с уравнением p ̂ = m’r + b’.
И последний способ — абсолютный
Квадратичный способ очень эффективен, но есть еще один полезный трюк — абсолютный метод, который является промежуточным решением между простым и квадратичным способами.
Используя квадратичный способ, мы применяли две величины — p-p̂ (цена — прогнозируемая цена) и r (количество комнат), чтобы свести четыре случая к одному.
Оперируя абсолютным значением, мы используем только r, чтобы свести четыре случая к двум.
Иными словами, если точка находится выше линии (т. е. если p>p̂)), можно выполнить следующие действия.
- Добавьте η к y-пересечению b. Получается b’ = b+η (это переместит линию вверх).
- Добавьте ηr к наклону m. Получается m’ = m+ηr (это повернет линию против часовой стрелки, если точка находится справа от оси y, и по часовой, если она расположена слева от оси y).
Если точка находится ниже линии (т. е. если p < p̂), можно сделать следующее.
- Вычтите η из y-пересечения b. Получается b’ = b-η (это переместит линию вниз).
- Вычтите ηr из наклона m. Получается m’ = m-ηr (это повернет линию по часовой стрелке, если точка находится справа от оси y, и против часовой, если она расположена слева от оси y).
Что делать дальше?
Выполняем квадратичный/абсолютный способ (простой способ был показан лишь для иллюстрации) несколько раз и приближаем линию к точкам.
Выражение “запустить несколько раз” означает запуск какого-либо элемента в цикле, а в МО каждая итерация в цикле называется “эпохой”.
Число для эпохи задается в начале или до запуска модели.
Итак, наша модель линейной регрессии теперь будет работать следующим образом.
- Начинать со случайных значений для наклона и y-пересечения.
- Повторять много раз (эпох):
- Выбирать случайную точку данных.
- Обновлять наклон и y-пересечение, используя абсолютный или квадратичный способ.
Так и получается алгоритм линейной регрессии!
Как насчет тестирования на наборе данных?
У меня был готовый набор данных из книги Луиса Серрано Grokking Machine Learning, и я мог проверить, как алгоритм будет смещаться или поворачиваться после каждой эпохи.
Я использовал описанные выше приемы, чтобы сформировать и определить линию (наш алгоритм линейной регрессии), и после 1000 эпох мы видим, как поворачивалась и перемещалась линия.
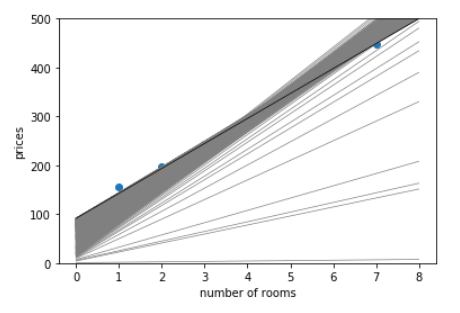
Вот что осталось невыясненным на данном этапе.
- Насколько сильно нужно корректировать веса?
- Сколько раз следует повторить процесс?
- Как узнать, что модель работает?
Чтобы рассмотреть эти вопросы, в следующей статье мы углубимся в такие понятия, как ошибка, минимизация ошибки и градиентный спуск.
Читайте также:
- Как использовать ИИ и Python для распознавания речи
- Генерирование синтетических обучающих данных с поддержкой масштабирования для задач NLP с помощью T0PP
- 6 техник, которые помогут вам учиться лучше
Читайте нас в Telegram, VK и Дзен
Перевод статьи Anushree Chatterjee: #02TheNotSoToughML | Tricks to ‘Fit a line’