Повторение статистики для начала путешествия по науке о данных
Часть 1, Часть 2, Часть 3, Часть 4, Часть 5
«Статистика — это грамматика науки»
Данное высказывание приписывают английскому математику Карлу Пирсону, который считается некоторыми основателем современной статистики.
Мы же поговорим о статистике в науке о данных.
Такие библиотеки машинного обучения, как Tensorflow или Scikit-learn, скрывают почти всю сложную математику от пользователей.
То есть нам не нужно особо разбираться в математике, но иметь общие, базовые знания все равно необходимо для более эффективного использования данных библиотек.
Я собираюсь написать пять коротких статей по следующим темам, чтобы начать, а затем сопровождать наше приключение по науке о данных:
Часть 1: Типы данных | Меры центральной тенденции | Меры изменчивости
Часть 2: Распределение данных
Часть 3: Меры расположения | Моменты случайной величины
Часть 4: Ковариация | Корреляция
Часть 5: Условная вероятность | Байесовская теорема
Что ж, приступим к первой части!
Типы данных
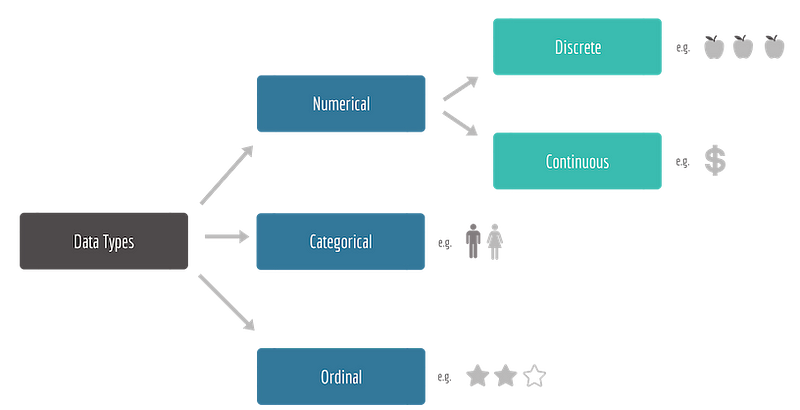
Самая базовая часть: данные делятся на три категории, основываясь на которых специалист по обработке данных выбирает, как проводить дальнейший анализ и обработку:
#1. Числовые данные представляют собой некоторую количественную информацию, которая поддается измерению и далее подразделяется на две подкатегории:
- Дискретные данные — основываются на целых числах (например, количество людей)
- Непрерывные данные — основываются на десятичных числах (например, цена, расстояние, температура).
#2. Категориальные данные — это качественные данные, применяемые для классификации данных по категориям (перечисление в программировании). Например, пол, марки автомобилей, страна проживания и т.д. Иногда категориям присваиваются номера для компактности, но они не имеют никакого математического значения.
#3. Порядковые данные представляют собой дискретные и упорядоченные единицы, например, места, занятые на Лиге чемпионов(1-е, 2-е, 3-е), приоритет ошибки (низкий, критический, showstopper), звезды у отеля (1–5).
Меры центральной тенденции
Представим, что у нас есть набор данных из пяти чисел:
{ 6, 3, 100, 3, 13 }
Среднее значение
Среднее значение (обозначаемое греческой буквой «мю» — μ) — некоторое число, заключенное между наименьшим и наибольшим значениями в наборе данных. Чтобы вычислить среднее значение, нужно сложить все значения и разделить получившуюся сумму на количество этих значений.
Напр: 6 + 3 + 100 + 3 + 13 = 125 →
μ = 125 ÷ 5 = 25
Медиана
Медиана — это середина набора данных. Чтобы вычислить медиану, необходимо рассортировать все значения (в порядке возрастания или убывания) и выбрать то значение, которое находится посередине.
Например: 3, 3, 6, 13, 100 → 6
Если количество точек данных четное, то для нахождения медианы просчитывается среднее значение двух точек по середине.
Медиана менее восприимчива к выбросам, чем среднее значение, и, следовательно, для выбора определенного значения мы должны принять во внимание то, как выглядит распределение данных.
Мода
Мода — это наиболее распространенное значение в наборе данных. Чтобы вычислить моду, необходимо найти число, которое встречается наиболее часто.
Например: 3:2, 6:1, 13:1, 100:1 → 3
Мода обычно важна для дискретных числовых данных, но не для непрерывных.
Меры изменчивости
Размах
Размах — это разница между наименьшим и наибольшим числами набора данных. Чтобы вычислить размах, необходимо вычесть наименьшее значение из наибольшего.
Например: 100 – 3 = 97
Результат показывает, насколько разнообразен набор данных, т.е. насколько он распространен. Но, как и среднее значение, размах очень чувствителен к выбросам.
Дисперсия
Дисперсия измеряет разброс данных. Чтобы вычислить дисперсию, необходимо взять среднюю точку квадратов разностей, полученных из среднего значения.
- #1. Найдите среднее значение точек данных
В пункте, где мы вычисляли среднее значение, это число составляло 25
- #2. Вычтите среднее значение из каждой точки данных.
6 - 25 = -19
3 - 25 = -22
100 - 25 = 75
3 - 25 = -22
13 - 25 = -12
- #3. Возведите в квадрат результат
(-19)^2 = 361
(-22)^2 = 484
(75)^2 = 5,625
(-22)^2 = 484
(-12)^2 = 144
- #4. Найдите среднее значение всех результатов (т.е. сложите все и разделите на количество)
361 + 484 + 5,625 + 484 + 144 = 7,098 →
7,098 ÷ 5 = 1,419.6
✏️«Сумма квадратов»
Существует две причины, почему на #3 этапе мы возводим результат в квадрат:
- Отрицательные разницы обладают тем же влиянием, что и положительные, т.е. они не исключают друг друга
- Это усиливает эффект, который есть у выбросов в наборе данных.
✏️ Полнота данных
На #4 этапе существует небольшое различие, зависимое от того, насколько полным является наш набор данных:
- Для полной совокупности мы делим на количество точек данных (n), т.е. #4 этап был правильным, так как в данном случае мы имеем полную совокупность
- Для выборок мы делим на количество точек данных минус 1 (n — 1)
7,098 ÷ 4 = 1774.5
Среднеквадратическое отклонение
Среднеквадратическое отклонение (обозначаемое греческой буквой «сигма» — σ) — это квадратный корень из дисперсии.
Например: σ = SQRT(1,419.6) = 37.68
Оно используется для того, чтобы узнать, какая точка данных является выбросом в зависимости от того, на сколько среднеквадратичных отклонений она далека от среднего значения.
В нашем случае значение 100 является выбросом:
μ = 25
σ = 37.68
Выбросы (верхняя граница): 25 + 37.68 = 62.68
Выбросы (нижняя граница): 25 - 37.68 = -12.68
Таким образом, значения больше, чем 62.68, и ниже, чем -12.68, являются выбросами.
Перевод статьи Semi Koen: Statistics is the Grammar of Data Science — Part 1






