Повторение статистики для начала путешествия по науке о данных
Часть 1, Часть 2, Часть 3, Часть 4, Часть 5
Меры расположения
Процентили
Процентили делят упорядоченные данные на сто равных частей. В рассортированных данных процентиль — это точка, показывающая процентное отношение значений в наборе данных, находящихся ниже данной точки.
50-й процентиль — это медиана.
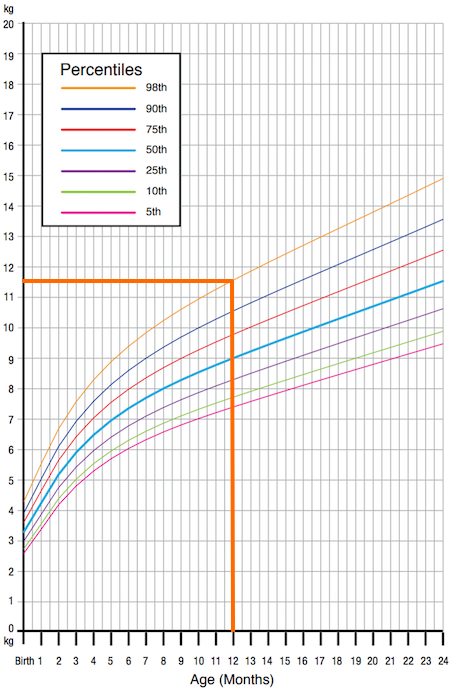
Например, на графике ниже показано развитие ребенка от рождения до 2 лет. Получается, что 98% развития ребенка за первый год жизни составляет в весе меньше 11,5 кг.
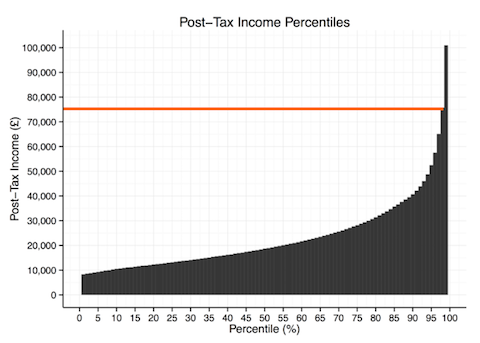
Другим примером является распределение доходов в стране. 99-й процентиль — это уровень дохода, при котором 99% населения зарабатывают меньше этого значения и 1% — больше. Так в Великобритании, как показано на графике ниже, 99-й процентиль составляет 75.000 фунтов стерлингов.
Квартили
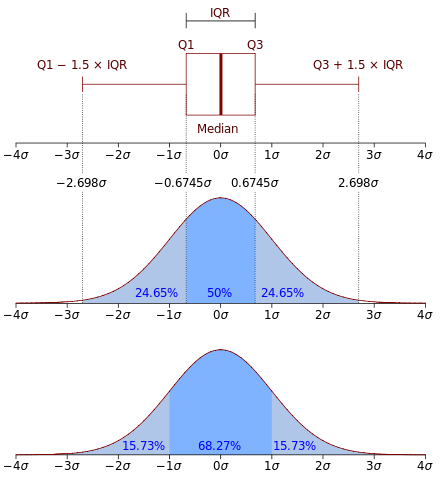
Квартили — это процентили, которые делят набор данных на четверти. Первый квартиль, Q1, равен 25-ому процентилю, третий квартиль, Q3, равен 75-ому процентилю. Медиана может быть обозначена либо вторым квартилем, Q2, либо 50-ым процентилем.
Интерквартильный размах (IQR)
IQR — число, которое показывает разброс средней половины (т.е. средние 50%) набора данных и помогает определить выбросы. IQR — это разница между Q3 и Q1.
IQR = Q3 - Q1
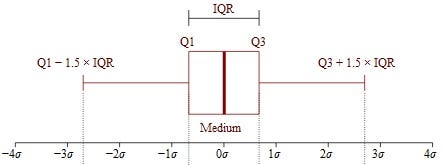
Выбросы — это, проще говоря, те значения данных, которые находятся за пределами следующих интервалов: Q1–1.5 x IQR и Q3 + 1.5 x IQR.
Диаграмма «ящик с усами»
Диаграмма «ящик с усами» показывает:
- насколько данные сконцентрированы;
- на каком расстоянии от большинства данных находятся точки экстремума.
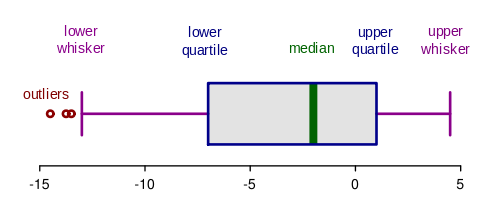
Ящик с усами имеет горизонтальную и вертикальную оси и прямоугольный ящик.
Минимальное и максимальное значения находятся на концах осей (в данном случае, это значения -15 и 5). Точка Q1 находится на одном конце ящика, Q3 — на другом.
«Усы» (выделенные фиолетовым цветом) начинаются с концов ящика и заканчиваются на самом минимальном или максимальном значениях данных. Также бывают ящики с усами, у которых есть отмеченные значения выбросов (выделены красным цветом). В таких случаях, усы не достигают минимального и максимального значений.
Ящики с усами на графике нормального распределения Ящики с усами на нормальных распределениях имеют некоторые особенности: Несмотря на то, что первый и третий квартили (Q1 и Q3) имеют такие названия, они, на самом деле, не составляют 25% от числа данных! Они показывают 34,135%. Также второй квартиль (Q2) составляет не 50%, а 68,27%.
Моменты случайной величины
Моменты случайно величины описывают различные аспекты характера и формы нашего распределения.
#1 — первый момент случайной величины — среднее значение данных, которое показывает место распределения.
#2 — второй момент случайной величины — дисперсия, которая показывает разброс распределения. Большие значения имеют больший размах, чем маленькие.
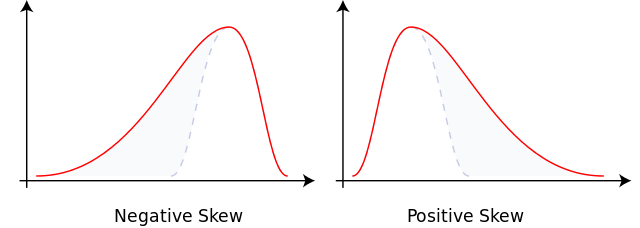
#3 — третий момент случайной величины — коэффициент асимметрии — мера того, насколько неравномерным является распределение. Коэффициент асимметрии положителен, если распределение наклонено влево и левый хвост короче правого. То есть среднее значение находится правее. И наоборот:
#4 — четвертый момент случайной величины — коэффициент эксцесса, который описывает то, насколько толстый хвост и насколько острый пик распределения. Этот коэффициент показывает, насколько вероятно найти точки экстремума в данных. Чем выше значение, тем вероятнее выбросы. Это похоже на разброс (дисперсию), но между ними есть отличия.
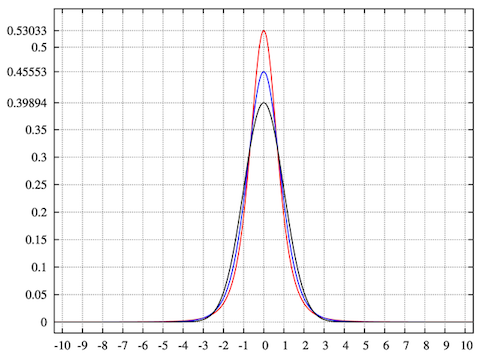
Как видно на графике, чем выше значение пики, тем выше коэффициент эксцесса, т.е. у верхней кривой коэффициент эксцесса выше, чем у нижней.
Перевод статьи Semi Koen: Statistics is the Grammar of Data Science — Part 3/5






