
Повторение статистики для начала путешествия по науке о данных
Часть 1, Часть 2, Часть 3, Часть 4, Часть 5
Введение
Предположим, у нас есть диаграмма рассеяния, на которой каждая точка — это человек. На одной оси показан его профессиональный опыт в годах, на другой — доход.
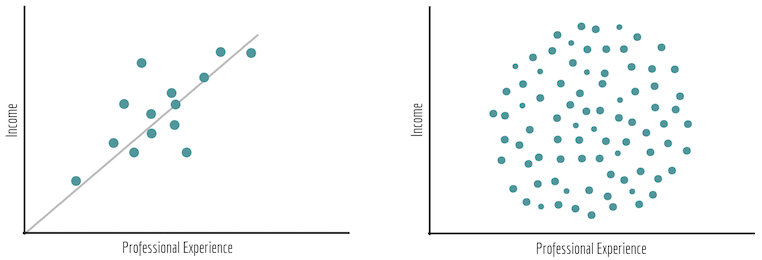
В соответствии с диаграммой справа можно заключить, что между опытом и доходом нет никакой связи, то есть определенный опыт оплачивается по-разному.
Слева, наоборот, между признаками существует четкая линейная зависимость.
Ковариация и корреляция показывают, насколько тесно между собой связаны переменные набора данных.
N.B: в приведенном примере представлен двумерный вид данных (с двумя переменными). На практике статистики используют многомерные данные (со множеством переменных).
Ковариация
Ковариация — это мера зависимости между двумя или более случайных переменных.
С английского «covariance» = «co» (совместность/соединение) + «variance» (дисперсия). То есть ковариация похожа на дисперсию, но она применяется для сравнения двух переменных, где вместо суммы квадратов, мы получаем сумму векторного произведения.
Дисперсия показывает, насколько определенная переменная отличается от среднего значения, а ковариация — насколько две переменные отличаются друг от друга. Таким образом, можно утверждать следующее:
Ковариация измеряет дисперсию между двумя переменными.
Ковариация может быть отрицательной, положительной и нулевой: положительное значение показывает, что две переменные изменяются в одном направлении (если одна переменная увеличивается, то и вторая тоже увеличивается); отрицательное значение показывает, что две переменные изменяются в разных направлениях (одна увеличивается, вторая уменьшается); нулевая ковариация означает, что они изменяются независимо друг от друга.
Формула
Формулу сложно объяснить, но важно понять, что она означает:
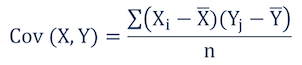
Предположим, что набор данных со случайными переменными представлен в виде вектора. Тогда в прошлом примере у нас есть два вектора для опыта и дохода. Ниже приведен порядок действий:
- #1. Преобразуйте данные два вектора в векторы отклонений от среднего значения.
- #2. Скалярное произведение двух векторов (которое равно косинусу угла между ними) поделите на размер выборки (n или n — 1, в зависимости от того, дана ли полная совокупность или нет).
На втором этапе измеряется угол между двумя векторами. Если угол острый, то переменные тесно связаны между собой.
Ограниченность
Следует отметить, что несмотря на то, что ковариация измеряет зависимость между направлениями двух переменных, она не показывает тесноту этой зависимости.
На практике самая большая проблема с этой мерой заключается в том, что она зависит от используемой единицы измерения. Например, необходимо перевести годы опыта в месяцы. Тогда ковариация будет в 12 раз больше.
В этом случае на помощь приходит корреляция!
Корреляция
Корреляция — одна из наиболее распространенных мер в статистике, описывающая тесноту взаимосвязи между двумя случайными переменными. Она считается нормализованной версией ковариации. Давайте рассмотрим, почему…
Формула
Корреляция (обозначаемая греческой буквой «ро» — ρ) рассчитывается по следующей формуле:
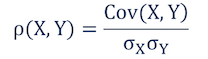
Корреляция ограничена в диапазоне от -1 до 1. Знак корреляции, как и ковариация, указывает направление взаимосвязи: положительное значение указывает на то, что случайные переменные движутся вместе, а отрицательное — в разные стороны.
Концы интервала (т.е. 1 и -1) указывают на то, что между двумя переменными существует функциональная связь. Например, взаимосвязь между метром и сантиметром заключается в том, что 1м. всегда соответствует 100 см. Если построить эту взаимосвязь на графике, то получится прямая. Тогда корреляция будет равна 1.
Обратите внимание, что функциональная связь редко встречается на практике, так как две случайные переменные обычно не сопоставляются друг с другом на основе постоянного значения.
Корреляция, равная 0, означает, что между двумя переменными нет линейной зависимости. Тогда может быть отношение x = y².
Ключевые свойства
Корреляция — безразмерная величина, указывающая не только на направление взаимосвязи, но и на ее тесноту (в зависимости от того, насколько большим является абсолютное значение). Единицы измерения исключены из-за того, что ковариацию разделили на среднеквадратическое отклонение.
Напоследок необходимо запомнить, что корреляция не является причинно-следственной связью. Высокая корреляция между двумя случайными переменными просто означает, что они связаны друг с другом, но их взаимоотношение не обязательно должен иметь причинно-следственный характер. Доказать причинно-следственную связь можно только с помощью контролируемых экспериментов, при которых внешние переменные исключаются и эффекты двух данных переменных изолируются.
Перевод статьи Semi Koen: Statistics is the Grammar of Data Science — Part 4/5






