Повторение статистики для начала путешествия по науке о данных
Часть 1, Часть 2, Часть 3, Часть 4, Часть 5
Функции распределения вероятностей
Функция распределения вероятностей — это функция, описывающая возможность того или иного события или результата. Мы разберем разные типы распределений в зависимости от вида набора данных: непрерывный или дискретный.
Функция плотности вероятности (PDF)
При графе, как на схеме ниже, можно подумать, что он показывает вероятность появления определенного значения. Однако, в случае с непрерывными данными все работает иначе, так как здесь мы имеем бесконечное количество точек данных. Таким образом, вероятность появления определенного значения может быть очень мала — бесконечно мала!
PDF показывает вероятность определенного ряда значений. Отсюда и слово «плотность»! Для визуализации вероятности необходимо отметить точки набора данных в виде кривой. Площадь под кривой между двумя точками соответствует вероятности того, что переменная окажется между этими двумя значениями.
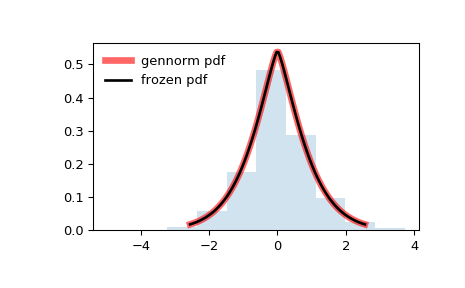
«Печально известное» колоколообразное стандартное нормальное распределение
Чтобы лучше разобраться в этом, рассмотрим особый случай PDF:
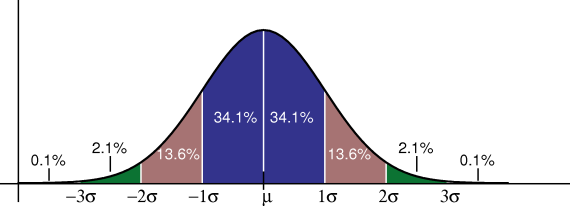
Между средним значением и одним среднеквадратичным отклонением (1σ) существует 34.1% вероятности того, что значение окажется в этом диапазоне. Таким образом, для данного значения существует 68,2% вероятности оказаться между точками -1σ и 1σ , то есть вероятность очень велика.
Это значит, что значения сконцентрированы рядом со средним значением, и по мере отдаления от одного среднеквадратичного отклонения (+-) вероятность постепенно уменьшается.
Функция распределения вероятности (PMF)
Когда речь заходит о дискретных данных, функция распределения вероятности является мерой, показывающей вероятность появления определенного значения. Для визуализации вероятности необходимо отметить точки набора данных в виде гистограммы.
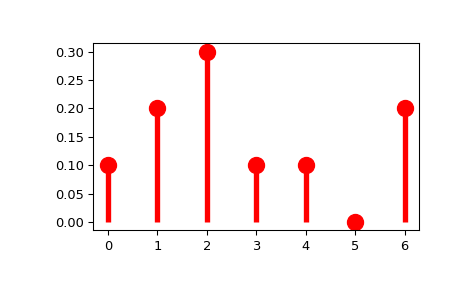
Непрерывные распределения данных
Теперь, когда мы узнали разницу между функцией плотности вероятности и функцией распределения вероятности, мы рассмотрим наиболее часто встречающиеся типы распределения, начиная с непрерывного.
#PDF-1: Равномерное / прямоугольное распределение
Равномерное распределение характеризуется наличием постоянной прямой вероятности значения на определенном интервале, а также оно связано с событиями, которые в равной степени вероятны.
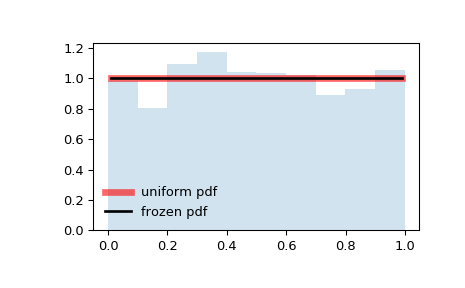
На данной диаграмме мы не получим результат ниже 0,0 и выше 1,0. Но в пределах данного диапазона есть прямая, так как существует постоянная вероятность того, что какое-нибудь значение попадет в заданный диапазон.
#PDF-2: Нормальное распределение / распределение Гаусса
Мы рассмотрели стандартное нормальное распределение, когда разбирали, что такое PDF. Если ввести случайный элемент, нормальное распределение будет выглядеть вот так:
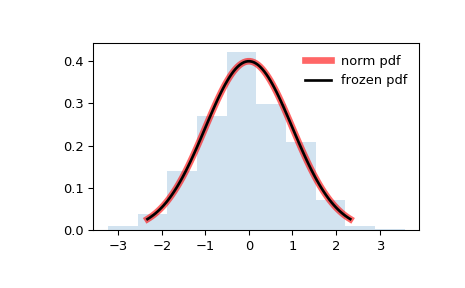
Среднее значение для стандартного нормального распределения равно 0, а среднеквадратичное отклонение — 1.
#PDF-3: Распределение Стьюдента
Распределение Стьюдента очень похоже на колоколообразную кривую нормального распределения, но немного короче и с более «тяжелыми» хвостами. Его используют вместо нормального распределения тогда, когда даны малые выборки и/или неизвестна дисперсия генеральной совокупности.
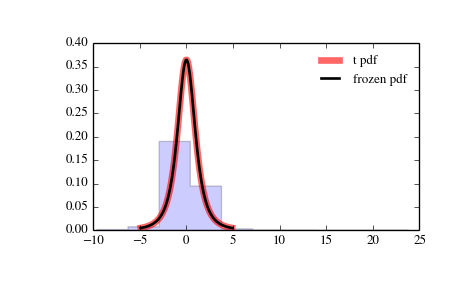
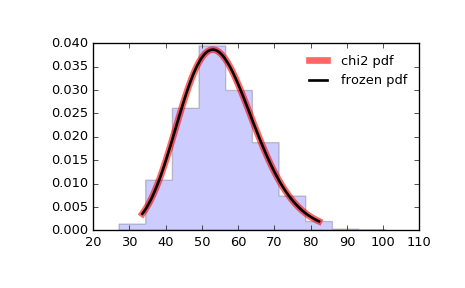
#PDF-4: Распределение χ2 (хи-квадрат)
Распределение χ 2 (хи-квадрат) используется для оценки следующих проблем:
- Подходит ли набор данных определенному виду распределения
- Одинаковы ли распределения двух совокупностей
- Независимы ли друг от друга два события
- Есть ли в совокупности другая изменчивость
Кривая стремится вправо.
#PDF-5: Экспоненциальное распределение вероятностей
Другой часто встречающейся функцией распределения является функция экспоненциального распределения вероятностей, в которой значения снижаются экспоненциально.
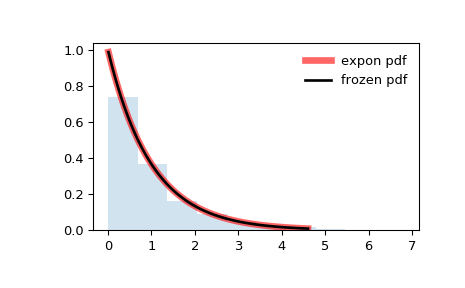
В таком распределении меньше больших значений и больше малых, то есть, чем событие ближе к нулю, тем вероятнее, что оно произойдет, и отдаляясь от нуля, вероятность события значительно сокращается.
Приведем пример из повседневной жизни — количество потраченных покупателями денег в магазине: гораздо больше людей, которые тратят небольшие суммы, чем тех, кто тратит огромные суммы денег.
Кроме того, такое распределение широко используется для построения времени, прошедшего между событиями, а также надежности, касающейся количества времени, в период которого продукт продолжает работать. Например, какое количество времени (начиная с этой минуты) в месяцах аккумулятор машины будет продолжать работать.
Дискретные распределения данных
Дискретные распределения данных делятся на два главных типа:
#PMF-1: Биномиальное распределение
Представим, что определенный эксперимент имеет два возможных результата: успех или провал. Допустим, эксперимент повторяли несколько раз, и эти повторы были независимы друг от друга. Общее число экспериментов, где результаты оказались успешными, является случайной переменной, распределение которой является биномиальным.
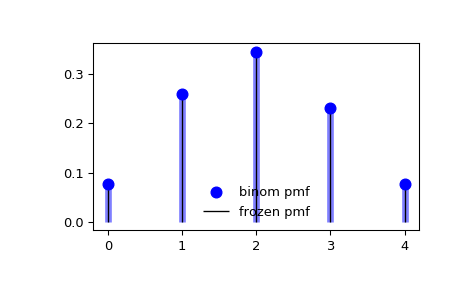
#PMF-2: Распределение Пуассона
Распределение Пуассона показывает вероятность определенных событий, происходящих за фиксированный временной интервал, если они совершаются:
- С известным средним значением
- Независимо по времени друг от друга
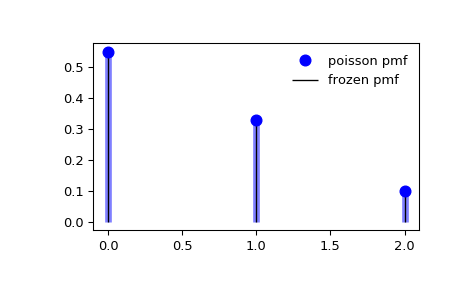
Классическим примером является количество телефонных звонков в call-центр.
Еще один способ, как использовать распределение Пуассона: если известно среднее количество происходящих событий в данный период времени, то можно спрогнозировать шансы того, получим ли мы другое значение в определенное время в будущем. Например: посты на “Medium” просматривают в среднем 1,000 человек в день. Я могу воспользоваться функцией распределения Пуассона, чтобы вычислить вероятность того, что когда-нибудь я наберу 1,500 просмотров.
Перевод статьи Semi Koen: Statistics is the Grammar of Data Science — Part 2/5






