“Не все, что блестит, — золото”. — Уильям Шекспир.
Предыдущие части: Часть 1, Часть 2, Часть 3.
В этой части мы ответим на вопрос:
Как узнать, что наша модель действительно работает?
Для этого нужно усвоить два очень важных для МО понятия:
Недообучение и переобучение.
Они часто дают о себе знать внезапно, перечеркивая всю работу над МО-моделью. Пока мы создаем модель — результаты выглядят вполне приемлемыми. Но стоит запустить ее в производство — оказывается, что наши решения были совершенно неправильными и модель плохо справляется с прогнозами.
Конечно, может быть множество факторов, способствующих “неправильным” результатам. Но чаще всего к таким сценариям приводит одна из двух оплошностей: недообучение или переобучение.
Мы подробно рассмотрим обе проблемы и найдем способы их решения. Хотя существует множество доступных методов, мы углубимся в следующие:
- тестирование и валидация модели;
- использование графа сложности модели.
Недообучение и переобучение — что это такое?
Хотя эти понятия можно интерпретировать по-разному, я предлагаю рассмотреть их как чрезмерное упрощение и чрезмерное усложнение МО.
Как?
Что ж, вот вам пример.

Скажем, перед вами стоит задача сразиться с Годзиллой. Что будет, если вы отправитесь на поле боя с мухобойкой? Это и есть пример чрезмерного упрощения.
Такой подход не пойдет нам на пользу, потому что мы недооценили проблему и пришли к ее решению неподготовленными. Это недообучение: когда наш набор данных сложен, и мы приходим к его моделированию, не имея ничего, кроме очень простой модели. Модель просто не сможет охватить все сложности набора данных.
Теперь рассмотрим другой пример.

Если нам надо убить крохотную муху, и мы собираемся это сделать, прихватив с собой противотанковый гранатомет, — это пример чрезмерного усложнения. Да, мы можем таким образом убить муху, но при этом уничтожим все вокруг и подвергнем себя риску. Мы переоценили проблему, и наше решение не было верным. Это переобучение: когда наши данные просты, но мы пытаемся подогнать их под слишком сложную модель. Модель сможет соответствовать нашим данным, но на самом деле она будет запоминать их, а не изучать.
Да, переобучение не выглядит такой серьезной проблемой, как недообучение. Однако самое большое препятствие, с которым мы сталкиваемся при переобучении моделей, — это неотображаемые данные. Прогнозы, скорее всего, будут ужасными! Мы поговорим об этом далее.
Каждая модель машинного обучения имеет гиперпараметры. Они представляют собой ручки управления, настраиваемые перед обучением модели. Установка правильных гиперпараметров имеет чрезвычайное значение для модели. В противном случае мы наверняка встретимся с последствиями недообучения или переобучения.
Теперь обратимся к нашим данным.
Рассмотрение недообучения-переобучения на примере полиномиальной регрессии
В предыдущих статьях я рассказывала, как найти наиболее подходящую строку для данных, предполагая, что эти данные очень похожи на линию. Но что, если данные не будут похожи на линию? В этом случае может быть полезно мощное расширение линейной регрессии, называемое полиномиальной регрессией, которое помогает справляться с более сложными данными.
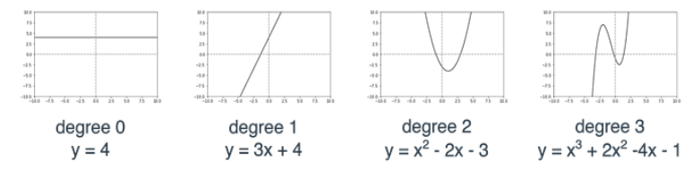
Все наши модели линейной регрессии, о которых мы говорили до сих пор, являются полиномиальными уравнениями степени 1.
Мы определяем степень полинома (многочлена) как показатель наивысшей степени в выражении полинома. Например, полином y = 2×3 + 8×2–40 имеет степень 3, поскольку 3 — это наивысший показатель, до которого повышается переменная x. Обратите внимание, что в приведенном выше примере полиномы имеют степень 0, 1, 2 и 3. Полином степени 0 всегда является константой, а полином степени 1 — линейным уравнением.
Граф полинома очень похож на кривую с несколькими колебаниями. Количество колебаний зависит от степени полинома. Если полином имеет степень d, то граф этого полинома представляет собой кривую, которая колеблется не более d-1 раз (для d>1).
Благодаря этой особенности полиномиальной регрессии, ее идеальный алгоритм позволяет увидеть, как недообучение/переобучение может повлиять на извлечение моделью уроков из данных и, в конечном счете, на наши прогнозы. Мы выясним это, настроив самый важный параметр в полиномиальной регрессии — ее степень.
Скажем, наши данные выглядят так:

Человеку будет достаточно приведенного выше изображения, чтобы заметить его схожесть с параболой (несколько напоминающей грустное лицо). Однако для компьютера идентифицировать это изображение как параболу будет непросто.
Предположим, компьютер пытается использовать различные степени полинома, чтобы соответствовать этим данным следующим образом:
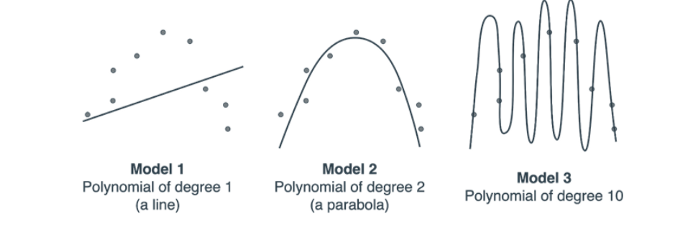
Обратите внимание на то, что Модель 1 слишком проста, так как это линия, пытающаяся соответствовать квадратичному набору данных. Мы никак не сможем найти подходящую линию для этого набора данных, потому что набор данных просто не похож на линию. Таким образом, Модель 1 является наглядным примером недообучения.
Модель 2, напротив, довольно хорошо соответствует данным. Об этой модели не скажешь, что она недообучена или переобучена.
Модель 3 очень хорошо соответствует данным, но она совершенно не передает сути. Данные должны выглядеть как парабола с небольшим шумом, а модель рисует очень сложный многочлен степени 10, которому удается пройти через каждую из точек, но не отражая сути данных. Модель 3 является наглядным примером переобучения.
Теперь рассмотрим следующую ситуацию. Напомню вывод предыдущей статьи: чтобы компьютер понял, какая модель является лучшей, ему просто нужно выбрать модель с наименьшей ошибкой. Но если бы это было так, то компьютер выбрал бы Модель 3, так как ее кривая удачнее всего передает расположение точек (они находятся на самой кривой!). Но мы знаем, что лучшая из трех — Модель 2!
Что делать в таком случае?
Нам нужно дать понять компьютеру, что Модель 2 — лучшая, а Модель 3 — слишком хороша.
Решение 1: Проведение тестирования и валидации
Тестирование модели заключается в выделении из набора данных небольшого набора точек, которые будут использоваться не для обучения модели, а для проверки производительности модели. Этот набор точек называется тестовым набором. Набор остальных точек (большинства), который мы используем для обучения модели, называется обучающим набором. После того как мы обучили модель на обучающем наборе, мы используем тестовый набор для оценки модели. Тем самым мы обеспечиваем способность модели обобщать неотображаемые данные, а не запоминать обучающий набор.
Теперь посмотрим, как этот метод будет работать с нашим набором данных и нашими моделями. Обратите внимание на то, что реальная проблема с Моделью 3 заключается не в том, что она не соответствует данным, а в том, что она плохо обобщает новые данные. Переформулирую проблему: если бы вы обучили Модель 3 на этом наборе данных, затем появилось бы несколько новых точек, вы бы доверили модели делать прогнозы с помощью этих новых точек? Вероятно, нет, поскольку модель просто запоминала весь набор данных, не улавливая его сути. В данном случае суть набора данных заключается в том, что он выглядит как парабола, направленная вниз.
Попробуем визуализировать обучающие и тестовые наборы для вышеуказанных моделей.
Мы можем использовать эту таблицу, чтобы решить, насколько сложной мы хотим видеть нашу модель.
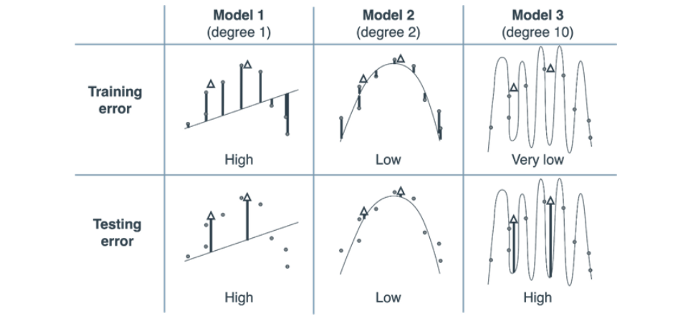
Колонки таблицы представляют три модели степени 1, 2 и 10. В таблице также представлены ошибки тестирования и обучения.
Закрашенные кружки — это обучающий набор, а белые треугольники — тестовый набор.
Ошибки в каждой точке можно увидеть в виде вертикальных линий от точки к кривой. Погрешность каждой модели — это средняя абсолютная погрешность (просто для ясности понимания), задаваемая средним значением этих вертикальных длин.
Обратите внимание на то, что ошибка обучения уменьшается по мере увеличения сложности модели. Однако ошибка тестирования уменьшается, а затем возвращается по мере увеличения сложности. Из этой таблицы мы делаем вывод: из трех моделей лучшей является Модель 2, так как она дает нам низкую ошибку тестирования.
Таким образом, чтобы оценить, насколько хорошо обучена модель (соответствует ли она требованиям либо недообучена/переобучена), нужно сравнить ошибки обучения и тестирования. Если обе ошибки высоки, то модель недообучена. Если обе ошибки невелики, то это правильно обученная модель. Если ошибка обучения низкая, а ошибка тестирования высокая, то модель переобучена.
Это наблюдение подводит нас к ЗОЛОТОМУ ПРАВИЛУ, которое ни в коем случае нельзя нарушать при работе с моделями МО:
“Никогда не используй тестовые данные для обучения”.
Разделяя данные на обучающий и тестовый наборы, мы должны использовать первый только для обучения модели и ни по какой причине не применять второй во время обучения модели или принятия решений по гиперпараметрам модели. Невыполнение этого требования, скорее всего, приведет к переобучению, даже если это не будет заметно для человека.
Теперь, когда вы знаете золотое правило, я скажу вам, что мы уже нарушили его в этой статье. Можете ли вы выяснить, где и как?
Именно здесь понадобится еще один набор данных, который является валидационным (контрольным) набором.
Валидационный набор
Напомню: у нас было три модели полиномиальной регрессии (1-й степени, 2-й степени и 10-й степени), и мы не знали, какую из них выбрать. Мы использовали наши обучающие данные для обучения трех моделей, а затем пустили в ход тестовые данные, чтобы решить, какую модель выбрать. Мы не должны использовать тестовые данные для обучения нашей модели или для принятия каких-либо решений по модели или ее гиперпараметрам. Иначе мы рискуем переобучить модель!
Что же мы теперь можем сделать? Решение простое: продолжаем разбивку набора данных. Вводим новый набор, валидационный, который затем будем использовать для принятия решений. Таким образом, мы разбиваем данные на следующие три набора:
- обучающий — для обучения всех наших моделей;
- валидационный — для принятия решений о том, какую модель использовать;
- тестовый — для проверки того, насколько хорошо работает выбранная модель.
Таким образом, в нашем примере должно было быть два момента проверки, и анализ ошибки валидации позволил бы решить, является ли Модель 2 наилучшей для использования. Тестовый набор следует применять только в самом конце, чтобы увидеть, насколько хороша наша модель. Если модель не очень хороша, я предлагаю все уничтожить и начать с нуля.
Объем этих наборов определяется множеством факторов, зависящих от объема самого набора данных. Наиболее часто практикуются разбивки на 60–20–20 или 80–10–10. Другими словами, 60% обучения, 20% валидации, 20% тестирования или 80% обучения, 10% валидации, 10% тестирования. Эти числа произвольны, но они, как правило, хорошо работают, так как оставляют большую часть данных для обучения, но все же позволяют нам протестировать модель в достаточно большом наборе.
Решение 2. Построение графа сложности модели
Представьте себе, что у нас есть другой набор данных, гораздо более сложный, и надо построить полиномиальную регрессионную модель, соответствующую этому набору данных. Мы пытаемся определить степень нашей модели в диапазоне от 0 до 10 (включительно). Как вы убедились в предыдущем разделе, ответом на вопрос, какую модель использовать, является выбор той, которая имеет наименьшую ошибку валидации.
Граф сложности модели — очень эффективный инструмент, помогающий определить идеальную сложность модели, чтобы избежать недообучения и переобучения.
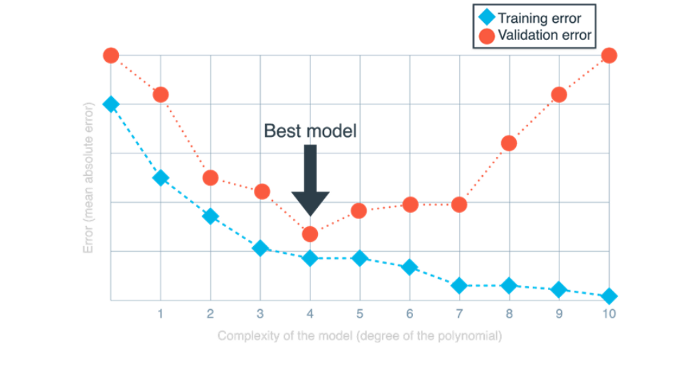
На приведенном выше графе горизонтальная ось представляет степень нескольких моделей полиномиальной регрессии от 0 до 10 (т. е. сложность модели). Вертикальная ось представляет собой ошибку, которая в данном случае определяется как средняя абсолютная ошибка.
Обратите внимание, что ошибка обучения начинается с большого значения и уменьшается по мере того, как мы движемся вправо. Это связано с тем, что чем сложнее наша модель, тем лучше она может соответствовать данным обучения. Однако ошибка валидации начинается с большого значения, затем уменьшается, а затем снова увеличивается. Это связано с тем, что очень простые модели не могут полностью соответствовать нашим данным (они недообучены), в то время как очень сложные модели соответствуют нашим данным обучения, но не нашим данным валидации, так как они переобучены.
Золотой серединой является идеальная точка, в которой модель не обнаруживает недообучения или переобучения, и мы можем найти ее, используя граф сложности модели.
Наименьшее значение валидационной ошибки имеет степень 4. Это означает, что для конкретного набора данных наиболее подходящей моделью (среди рассматриваемых нами) является полиномиальная регрессионная модель степени 4. Глядя на левую часть графа, мы видим: когда степень полинома очень мала, как ошибка обучения, так и ошибка валидации велики, что является показателем недообучения моделей. Глядя на правую часть графика, мы видим: ошибка обучения становится все меньше и меньше, а ошибка валидации становится все больше и больше, что означает, что модели переобучены. Самые оптимальные показатели находятся около 4 — это и есть модель, которую мы выберем.
Одним из преимуществ графа сложности модели является то, что, независимо от объема набора данных или количества тестируемых моделей, он всегда выглядит как две кривые, одна из которых всегда опускается (ошибка обучения), другая опускается, а затем возвращается (ошибка валидации). Конечно, в большом и сложном наборе данных эти кривые могут колебаться и поведение моделей труднее обнаружить. Тем не менее, граф сложности модели всегда будет полезным инструментом для исследователей данных. На таком графе легко найти оптимальное место и решить, насколько сложными должны быть модели, чтобы избежать как недообучения, так и переобучения.
Читайте также:
- Как распознавать объекты 600 классов, используя 9 миллионов изображений из Open Images
- 8 лучших платформ и библиотек JavaScript для машинного обучения
- Топ-10 курсов по машинному и глубокому обучению в 2020
Читайте нас в Telegram, VK и Дзен
Перевод статьи Anushree Chatterjee, #TheNotSoToughML | “Go, minimize the error” — But, is that enough?






