Наука о данных

Алгоритм машинного обучения t-SNE - отличный инструмент для снижения размерности в Python

12.01.2022

Визуализация t-SNE с различной степенью перплексии (искаженности). Gif-изображение автора.

Вступление

Продвинутый специалист в области обработки данных владеет широким спектром алгоритмов машинного обучения и может разъяснить результаты работы каждого алгоритма заинтересованным лицам. Однако не у каждого заинтересованного лица достаточно квалификации, чтобы понять эти разъяснения из-за сложности МО. К счастью, их можно сделать наглядными, используя методы уменьшения размерности для создания визуального представления данных высокой размерности.

В этой статье вы познакомитесь с одним из таких методов. Он называется t-SNE, что расшифровывается как t-distributed stochastic neighbor embedding (стохастическое вложение соседей с t-распределением).

Содержание

Место t-SNE в мире алгоритмов машинного обучения.
Интуитивно понятное объяснение механизма работы t-SNE.
Пример использования t-SNE в Python.

Стохастическое вложение соседей с t-распределением (t-SNE) в мире алгоритмов машинного обучения

Доскональная категоризация методов машинного обучения не всегда возможна. Это объясняется эксплуатационной гибкостью некоторых алгоритмов, используемых для решения различных задач (например, k-NN используется для регрессии и классификации).

Все же иногда полезно привнести некую структурированность в огромный мир МО. Приведенный ниже интерактивный граф является моей попыткой сделать именно это.

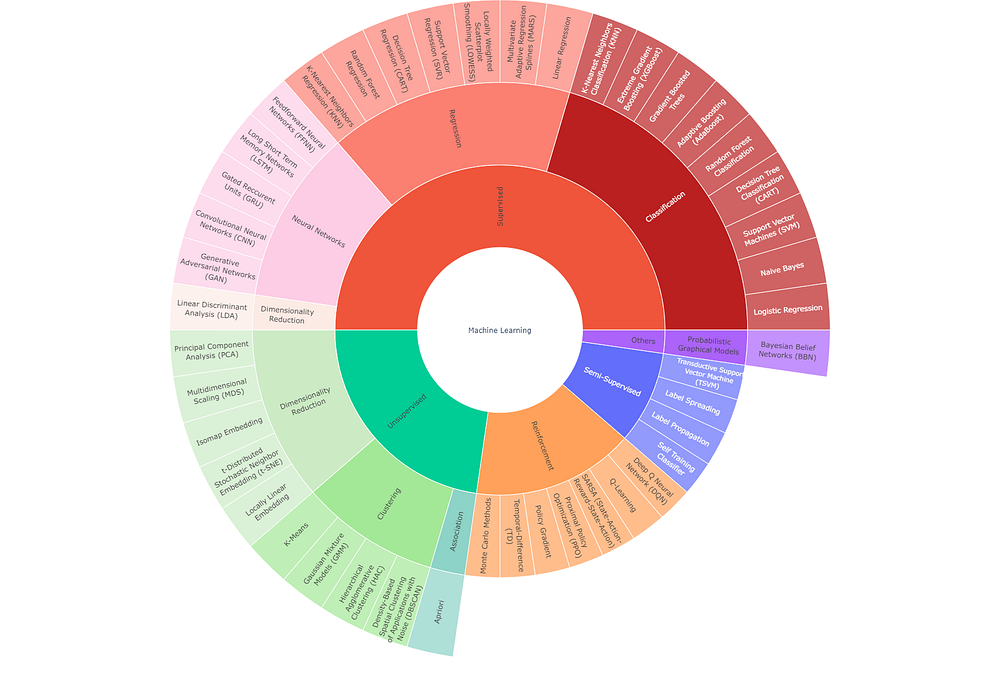
Классификация алгоритмов машинного обучения

Как видно на графике, t-SNE — метод уменьшения размерности, который относится к неконтролируемой ветви алгоритмов машинного обучения. Для использования таких — неконтролируемых — алгоритмов не нужно иметь маркированные данные (в отличие от контролируемых, таких как LDA — линейный дискриминантный анализ).

Хотя это не проиллюстрировано на приведенном графике, стоит знать, что методы уменьшения размерности можно дополнительно разделить на два типа:

Параметрический — создающий явную функцию отображения, которую можно использовать для тестовых данных, т.е. для определения местоположения новых точек во вложении с более низкой размерностью (например, PCA);
Непараметрический — не создающий явной функции отображения, т.е. не способный точно отобразить новые точки во вложении с более низкой размерностью. Тем не менее, на практике можно создать обходные пути для обеспечения такого отображения новых точек.

t-SNE относится к непараметрической группе методов. Следовательно, в основном он используется в целях визуализации.

Как работает стохастическое вложение соседей с t-распределением (t-SNE)

Анализ названия метода t-SNE

Чтобы составить общее представление о работе алгоритма, начнем с анализа названия t-SNE.

Обратите внимание на то, что приведенные ниже определения не являются общепринятыми. Однако эти упрощенные интерпретации сложных терминов помогут вам понять ключевые идеи, лежащие в основе t-SNE:

вложение — многомерные данные, представленные в пространстве меньшей размерности;
сосед — точка данных, расположенная близко к интересующей нас точке данных;
стохастический — случайно используемый в итерационном процессе при поиске репрезентативного вложения;
t-распределение — распределение вероятности, используемое алгоритмом для вычисления оценок сходства в низкоразмерном вложении.

Соединив вышеприведенные определения, можно описать t-SNE как метод, который использует поэтапный итерационный подход для низкоразмерного представления исходных данных с сохранением информации об их локальном соседстве.

Обратите внимание, что для общего понимания этого алгоритма не стоит уделять много внимания элементу вероятностного распределения. t-распределение, используемое на 2-м и 3-м этапе, отличается “более плоской” формой с “более высокими” “хвостами”. Такая форма позволяет распределить точки в пространстве с более низкой размерностью. В противном случае вы можете получить кучу точек, нагроможденных друг на друга.

Этапы работы алгоритма t-SNE

Этап 1

t-SNE начинается с определения сходства точек на основе расстояний между ними. Близлежащие точки считаются похожими, в то время как удаленные считаются непохожими.

Для этого измеряются расстояния между интересующей точкой и другими точками, после чего они помещаются на нормальную кривую. Такие измерения проделываются для каждой точки с применением некоторого масштабирования для учета различий в плотности различных секций.

Например, на приведенной ниже иллюстрации мы наблюдаем более высокую плотность в секции, занятой синими точками, и более низкую плотность в секции, занятой желтыми точками.

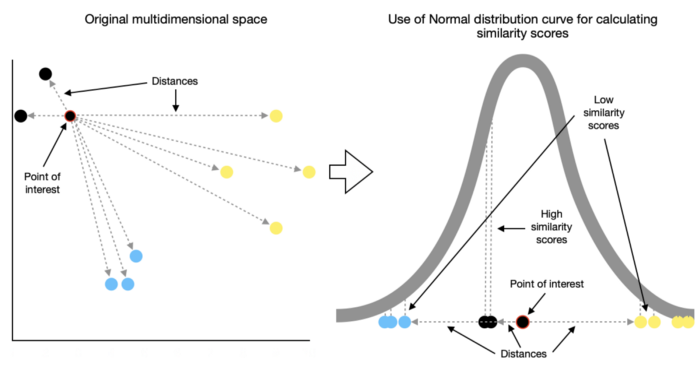
Результатом этих вычислений является матрица, содержащая оценки сходства между каждой парой точек из исходного многомерного пространства.

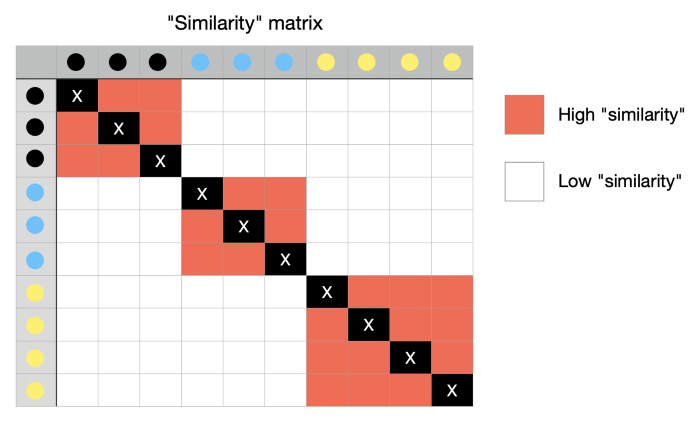
Этап 2

Далее переходим к t-SNE, который рандомно отображает все точки в более низкоразмерном пространстве и вычисляет сходство между ними, как описано выше. Правда, с одним отличием: на этот раз алгоритм использует t-распределение вместо нормального распределения.

Неудивительно, что новая матрица сходства значительно отличается от исходной из-за рандомного отображения. Вот пример того, как это может выглядеть.

Пример того, как может выглядеть новая матрица “сходства”

Этап 3

Теперь цель алгоритма состоит в том, чтобы создать новую матрицу сходства, похожую на исходную, используя итерационный подход. С каждой итерацией точки перемещаются к своим ближайшим соседям из исходного многомерного пространства и удаляются от отдаленных.

Новая матрица сходства постепенно начинает больше походить на исходную. Процесс продолжается до тех пор, пока не будет достигнуто максимальное количество итераций или предельное улучшение.

Описание этого процесса в сугубо научных терминах выглядит так: алгоритм минимизирует расхождение Кульбака–Лейблера (расхождение KL) посредством градиентного спуска.

Перплексия

Один важный аспект, о котором я еще не упомянул, — это гиперпараметр, известный как перплексия. Он описывает ожидаемую плотность вокруг каждой точки или, другими словами, устанавливает соотношение целевого количества ближайших соседей к интересующей точке.

Параметр перплексии играет важнейшую роль в определении конечного результата вложения. Как правило, можно выбрать значение перплексии где-то между 5 и 50, но при этом обязательно следует поэкспериментировать с другими значениями.

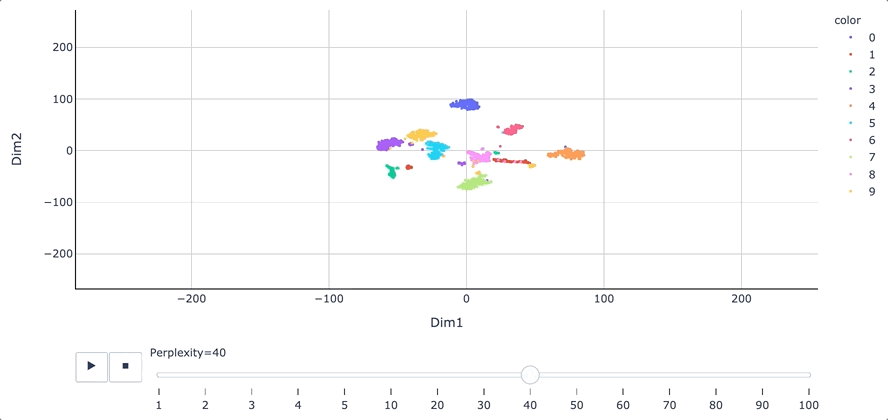
В начальную часть статьи я включил gif-изображение, чтобы продемонстрировать, как меняется окончательная визуализация при использовании разных значений перплексии. Низкое значение заставляет алгоритм фокусироваться на меньшем количестве соседей, что приводит ко множеству небольших групп. Напротив, высокое значение перплексии расширяет горизонт соседства, что приводит к уменьшению числа более плотно упакованных групп.

Как использовать t-SNE в Python?

Теперь, когда вы поняли механизм работы алгоритма, самое время поговорить об использовании его в Python.

Применим t-SNE к набору данных MNIST (набору рукописных цифр), чтобы увидеть, насколько успешно визуализируются данные высокой размерности.

Настройка

Будем использовать следующие данные и библиотеки:

Scikit-learn библиотека для:
1) данных образцов цифр MNIST из набора данных sklearn (load_digits);
2) выполнения уменьшения размерности (t-SNE);
Plotly и Matplotlib для визуализации данных;
Pandas для манипулирования данными.

Первым шагом является импорт библиотек, которые мы перечислили выше:

# Манипулирование данными
import pandas as pd # для манипулирования данными

# Визуализация
import plotly.express as px # для визуализации данных
import matplotlib.pyplot as plt # для отображения рукописных цифр

# Sklearn
from sklearn.datasets import load_digits # для данных MNIST
from sklearn.manifold import TSNE # для снижения размерности с помощью t-SNE

Затем загружаем данные MNIST:

# Загрузка данных образцов цифр
digits = load_digits()

# Загрузка массивов, содержащих данные образцов цифр (64 пикселя на изображение) и их истинных меток
X, y = load_digits(return_X_y=True)

# Статистические данные
print('Shape of digit images: ', digits.images.shape)
print('Shape of X (training data): ', X.shape)
print('Shape of y (true labels): ', y.shape)

Теперь выведем первые десять написанных от руки цифр, чтобы лучше понимать, с чем мы работаем.

# Отображение изображений первых 10 цифр
fig, axs = plt.subplots(2, 5, sharey=False, tight_layout=True, figsize=(12,6), facecolor='white')
n=0
plt.gray() 
for i in range(0,2):
    for j in range(0,5):
        axs[i,j].matshow(digits.images[n])
        axs[i,j].set(title=y[n])
        n=n+1
plt.show()

Изображения первых десяти написанных от руки цифр (8×8=64 пикселя, т.е. 64-мерные изображения)

Применение t-SNE к выбранным данным

На предыдущем шаге мы загрузили данные в массив X формы (1797,64), что означает, что у нас 1797 цифр, каждая из которых является 64-мерной.

Теперь будем использовать t-SNE, чтобы уменьшить размерность с 64 до 2. Обратите внимание, что я использую значения по умолчанию для большинства гиперпараметров. Я также включил краткие пояснения к каждому параметру, чтобы вы могли поэкспериментировать, опробовав различные настройки.

# Настройка функции t-SNE.
embed = TSNE(
    n_components=2, # значение по умолчанию=2. Размерность вложенного пространства.
    perplexity=10, # значение по умолчанию=30.0. Перплексия связана с количеством ближайших соседей, которое используется в других алгоритмах обучения на множествах.
    early_exaggeration=12, # значение по умолчанию=12.0. Определяет, насколько плотными будут естественные кластеры исходного пространстве во вложенном пространстве и сколько места будет между ними. 
    learning_rate=200, # значение по умолчанию=200.0. Скорость обучения для t-SNE обычно находится в диапазоне [10.0, 1000.0]. Если скорость обучения слишком высока, данные могут выглядеть как "шар", в котором любая точка приблизительно равноудалена от ближайших соседей. Если скорость обучения слишком низкая, большинство точек могут быть похожими на сжатое плотное облако с незначительным количеством разбросов. 
    n_iter=5000, # значение по умолчанию=1000. Максимальное количество итераций для оптимизации. Должно быть не менее 250.
    n_iter_without_progress=300, # значение по умолчанию=300. Максимальное количество итераций без прогресса перед прекращением оптимизации, используется после 250 начальных итераций с ранним преувеличением.
    min_grad_norm=0.0000001, # значение по умолчанию=1e-7. Если норма градиента ниже этого порога, оптимизация будет остановлена.
    metric='euclidean', # значение по умолчанию='euclidean', Метрика, используемая при расчете расстояния между экземплярами в массиве признаков.
    init='random', {'random', 'pca'} или ndarray формы (n_samples, n_components), значение по умолчанию='random'. Инициализация вложения.
    verbose=0, # значение по умолчанию=0. Уровень детализации.
    random_state=42, # экземпляр RandomState или None, по умолчанию=None. Определяет генератор случайных чисел. Передача int для воспроизводимых результатов при многократном вызове функции.
    method='barnes_hut', # значение по умолчанию='barnes_hut'. По умолчанию алгоритм вычисления градиента использует аппроксимацию Барнса-Хата, работающую в течение времени O(NlogN). метод='exact' будет работать по более медленному, но точному алгоритму за время O(N^2). Следует использовать точный алгоритм, когда количество ошибок ближайших соседей должно быть ниже 3%.
    angle=0.5, # значение по умолчанию=0.5. Используется только если метод='barnes_hut' Это компромисс между скоростью и точностью в случае T-SNE с применением алгоритма Барнса-Хата.
    n_jobs=-1, # значение по умолчанию=None. Количество параллельных заданий для поиска соседей. -1 означает использование всех процессоров.
)

# Преобразование X
X_embedded = embed.fit_transform(X)

# Вывод результатов
print('New Shape of X: ', X_embedded.shape)
print('Kullback-Leibler divergence after optimization: ', embed.kl_divergence_)
print('No. of iterations: ', embed.n_iter_)
#вывод('Embedding vectors: ', embed.embedding_)

Приведенный выше код выводит основные статистические данные:

Основные статистические данные из полученного вложения t-SNE

Наконец, давайте построим новый массив X в виде 2-мерной диаграммы разброса. Обратите внимание, что при ее создании использованы различные цвета для представления фактических меток цифр. Это помогает увидеть, как сходные цифры группируются вместе.

# Создание диаграммы разброса
fig = px.scatter(None, x=X_embedded[:,0], y=X_embedded[:,1], 
                 labels={
                     "x": "Dimension 1",
                     "y": "Dimension 2",
                 },
                 opacity=1, color=y.astype(str))

# Изменение цвета фона графика
fig.update_layout(dict(plot_bgcolor = 'white'))

# Обновление линий осей
fig.update_xaxes(showgrid=True, gridwidth=1, gridcolor='lightgrey', 
                 zeroline=True, zerolinewidth=1, zerolinecolor='lightgrey', 
                 showline=True, linewidth=1, linecolor='black')

fig.update_yaxes(showgrid=True, gridwidth=1, gridcolor='lightgrey', 
                 zeroline=True, zerolinewidth=1, zerolinecolor='lightgrey', 
                 showline=True, linewidth=1, linecolor='black')

# Установка названия рисунка
fig.update_layout(title_text="t-SNE")

# Обновление размера маркера
fig.update_traces(marker=dict(size=3))

fig.show()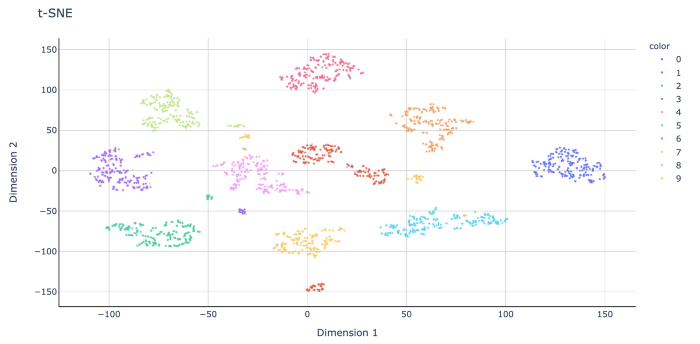

2D t-SNE-вложение 64-мерных образцов данных цифр MNIST

Мы видим, что алгоритм t-SNE проделал довольно хорошую работу по выявлению схожих цифр, причем большинство из них образовали плотные группы. Однако есть несколько небольших кластеров, а именно 1 (красный), 3 (фиолетовый) и 9 (желтый), которые, по-видимому, довольно далеки от своих основных групп. Такие результаты могут указывать на существование различных способов написания одной и той же цифры.

Заключение

t-SNE — отличный инструмент для визуализации сходства между различными точками данных. С его помощью можно провести анализ различными способами.

Например, он поможет определить различные варианты написания одной и той же цифры или найти синонимы слов / фразы со схожим значением при выполнении анализа НЛП. Вы также можете использовать его в качестве наглядного пособия при объяснении выполненного анализа заинтересованным сторонам.

Однако, как и любой алгоритм МО, t-SNE имеет определенные ограничения, которые необходимо учитывать при его использовании:

t-SNE предполагает непараметрический подход к уменьшению размерности, то есть алгоритм не создает явной функции отображения для использования относительно новых точек данных.
Возможно, вам придется поэкспериментировать с различными значениями перплексии, чтобы найти то, которое лучше всего подходит для ваших данных.
Вы можете получать разные результаты после каждого запуска из-за случайной инициализации и стохастического характера. Если вам нужны воспроизводимые результаты, обязательно укажите начальное значение (random_state).

Алгоритм машинного обучения t-SNE - отличный инструмент для снижения размерности в Python

Вступление

Содержание

Стохастическое вложение соседей с t-распределением (t-SNE) в мире алгоритмов машинного обучения

Как работает стохастическое вложение соседей с t-распределением (t-SNE)

Анализ названия метода t-SNE

Этапы работы алгоритма t-SNE

Этап 1

Этап 2

Этап 3

Перплексия

Как использовать t-SNE в Python?

Настройка

Применение t-SNE к выбранным данным

Заключение

Читайте также

Понятие об умных указателях Rust

Автоматизируйте код-ревью и ускорьте итерации

Уникальный пример использования SocketCluster для распределенных вычислений

Тесты

Что вы знаете о типах данных Java?

Насколько хорошо вы разбираетесь в Kotlin?

Насколько вы знакомы с языком Swift