Часть 1, Часть 2, Часть 3, Часть 4, Часть 5
Условная вероятность
Условная вероятность — это вероятность наступления некоторого события, при условии, что другое событие уже произошло.
Условная вероятность обозначается через P(A|B), которое читается как «вероятность А при условии В». Она вычисляется по формуле:
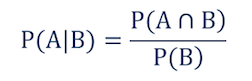
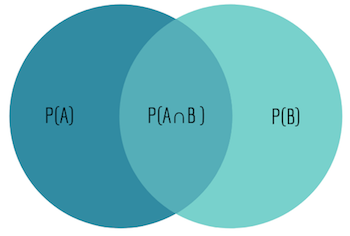
A ∩ B — это пересечение событий А и В на диаграмме Венна. Таким образом, P(A∩B) — это вероятность того, что оба события — А и В — произойдут.
Следовательно:
Вероятность события А при условии В равно вероятности событий А и В, деленной на вероятность В.
Пример:
Предположим, из мешка достают три шарика: красный, зеленый и синий.
Какова условная вероятность того, что после красного шарика из мешка достанут синий?
Если событие А — это событие, при котором первым достают красный шарик, а событие В — это событие, при котором достают синий шарик, то нам нужно найти P(A∩B):
- P(A) — это вероятность того, что в первую очередь достанут красный шарик. Так как это один из трех возможных результатов, то далее мы имеем:
P(A) = 1/3 = 33.33%
- P(B|A) — это вероятность того, что вторым достанут синий шарик. Так как у нас останется два шарика, то получается:
P(B) = 1/2 = 50%
- P(A ∩ B) — это вероятность того, что первым достанут красный шарик, а вторым — синий:
P(A ∩ B) = P(A) * P(B|A) = 33.33% * 50% = 16.66%
Для визуализации воспользуемся древовидной диаграммой: у каждой ветки есть условная вероятность
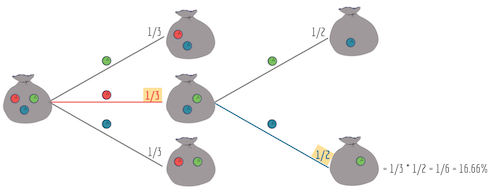
Причинно-следственная связь
Причинно-следственная связь описывается в четвертой части. Условная вероятность не указывает на то, что между данными двумя события обязательно существует причинно-следственная связь, а также на то, что два события произойдут одновременно.
Независимые события
Независимыми называются такие события, исход которых не влияет на вероятность исхода другого события. Следовательно:
P(A|B) = P(A)
P(B|A) = P(B)
Взаимоисключающие события
Взаимоисключающими называются такие события, которые не могут произойти одновременно, т.е. если одно событие уже произошло, то другое произойти не может. Следовательно:
P(A|B) = 0
P(B|A) = 0
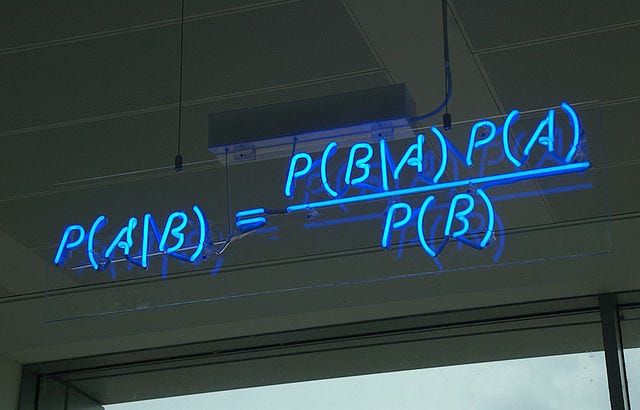
Теорема Байеса
После условной вероятности, давайте рассмотрим теорему Байеса. Она гласит:
Вероятность события А при условии В равна вероятности события В при условии А, умноженной на вероятность события А и деленной на вероятность В.
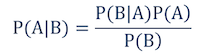
Другими словами, она позволяет удобно найти зависимость P(A|B) и P(B|A) друг от друга.
Теорема Байеса является фундаментом целого направления в статистике («Байесовская статистика»). Она применяется во многих дисциплинах, например, ярким примером служит медицинская и фармакологическая сферы, а также финансовая (для прогноза вероятности успеха каких-либо вложений).
Количество почти так же важно, как и качество, при применении этих условных переменных к теореме Байеса. Например, необходимо просчитать риск кредитования заемщика. Если учесть другие вероятности, такие как возраст заемщика, его кредитоспособность и готовность к принятию риска, то возможность получения кредита для разных лиц может отличаться.
Теорема допускает следующее:
Чем больше переменных учитывается и чем больше в нас уверенности в переменных, тем точнее будет вывод при использовании условных вероятностей.
Пример:
Представим, что мы врачи некоторой больницы и мы знаем следующее: — вероятность того, что у пациента заболевание печени, равна 20%; — вероятность того, что пациент болен алкоголизмом — 5%; вероятность того, что среди тех пациентов, у которых диагностировали заболевание печени, есть больные алкоголизмом — 10%. Теперь найдем:
Какова условная вероятность того, что пациент с заболеванием печени — болен алкоголизмом?
- P(A) — вероятность наличия заболевания печени:
P(A) = 20%
- P(B) — вероятность того, что пациент болен алкоголизмом:
P(B) = 5%
- P(B|A) — условная вероятность того, что пациент болен алкоголизмом при условии заболевания печени:
P(B|A) = 10%
- P(A|B) — это условная вероятность того, что у пациента заболевание печени при условии, что он болен алкоголизмом:
P(A|B) = (10% * 20%) / 5% = 40%
Взаимоисключающие события
Частным случаем теоремы Байеса является то, когда событие А — это двоичное значение. В таком случае «А-» обозначает то, что событие А произошло, и «А+» — не произошло (т.е. события А- и А+ являются взаимоисключающими)
Формула:
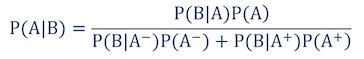
Точность
Истинно положительный случай — это результат, при котором модель правильно прогнозирует положительный класс. Так же истинно отрицательный случай — это результат, при котором модель правильно прогнозирует отрицательный класс.
Ложноположительный случай — это результат, при котором модель неправильно прогнозирует положительный класс. Так же ложноотрицательный случай — это результат, при котором модель неправильно прогнозирует отрицательный класс.
Чувствительность показывает вероятность того, что тест правильно спрогнозирует положительный класс → истинно положительные случаи.
Специфичность показывает вероятность того, что тест правильно спрогнозирует отрицательный класс → истинно отрицательные случаи.
Чувствительность = истинно положительные случаи / (истинно положительные + ложнооттрицательные)
Специфичность = истинно отрицательные случаи / (истинно отрицательные + ложноположительные)
Пример:
Предположим, что определенное заболевание имеет коэффициент заболевания 2%. Если ложноотрицательный коэффициент равен 10%, а ложноположительный — 1%, то:
Какова условная вероятность того, что человек с положительным результатом теста на самом деле болен?
Если событие А — это событие, при котором человек болен, а событие В — это событие, при котором результаты теста положительны, то необходимо вычислить P(A|B), т.е. несмотря на положительный результат теста (В), человек окажется болен (А).
- P(A+) или P(A) — это вероятность наличия заболевания:
P(A+) = 2%
- P(A–) — это вероятность отсутствия заболевания, которая высчитывается следующим образом:
P(A-) = 100% - 2% = 98%
- P(B|A–) — это вероятность ложноположительного случая, т.е. человек здоров (А-), но результат теста положительный (В):
P(B|A-) = 1%
- P(B–|A) — это вероятность ложноотрицательного случая, т.е. человек болен (А), но результат теста отрицательный (В-):
P(B-|A) = 10%
- P(B|A+) или P(B|A) — это истинно положительный случай, т.е. человек болен (А) и результат теста положительный (В). Высчитывается это следующим образом:
P(B|A) = 100% - 10% = 90%
- Теперь у нас есть вся необходимая информация, чтобы найти P(A|B):
P(A|B) = [ P(B|A) x P(A) ] / [ P(B|A-) x P(A-) + P(B|A+) x P(A+) ]
= [ 90% x 2% ] / [ 1% x 98% + 90% x 2% ] =
= 64.7%
Для визуализации точности теста можно использовать матрицу:
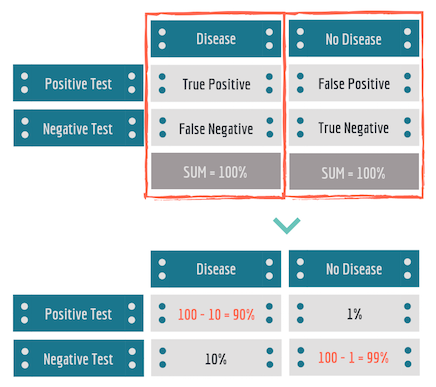
И древовидную диаграмму:
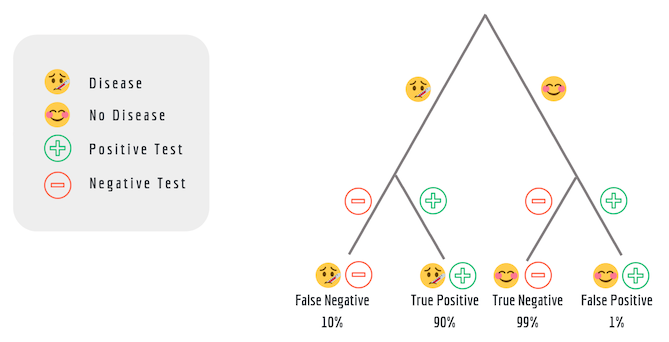
Конец

Перевод статьи Semi Koen: Statistics is the Grammar of Data Science — Part 5/5