Зачем это нужно
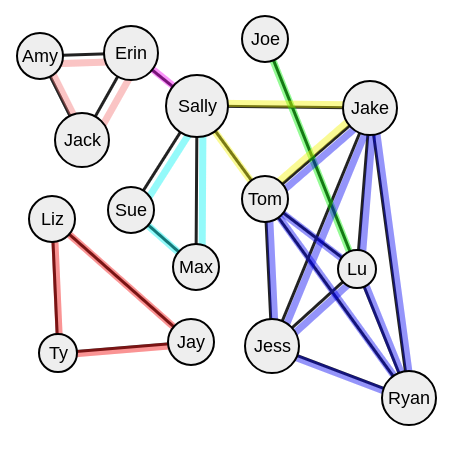
Сэлли устраивает вечеринку.? Она пригласила Макса, Сью, Тома и Джейка. Потом Том позвал Райна, который пришел с Джесс, а Джесс позвала Лу, который знает друзей Тома. Джейк очень общительный, поэтому он тоже знаком с Джесс и Райаном. А ещё пришёл Джо. Джо знаком с Лу, но не знаком с Сэлли, и на самом деле не знает больше никого из гостей, но тем не менее, теоретически, он тоже приглашенный гость. Пришли ещё три случайных гостя — Лиз, Ти и Джей, — потому что вечеринка обещает быть шумной. В конце концов Эрин, которая как всегда очень элегантно опаздывает, приходит вместе с Эми и Джеком.
Наша задача — найти все максимальные группы людей, в которых все знают друг друга.
Давайте применим основной алгоритм Брона-Кербоша к данной системе социальных взаимоотношений, или, иными словами, давайте решим данную задачу, применив к вечеринке метод рекурсивного поиска с возвратом при O(3^n/3). NP-полные задачи решаются быстро, но сложно. Поэтому решим нашу задачу с помощью подграфов.
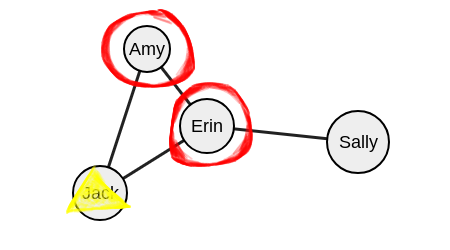
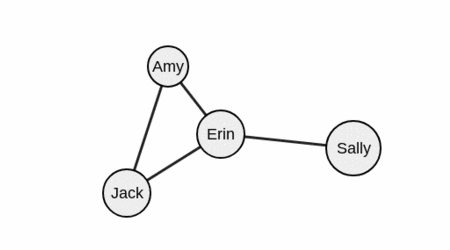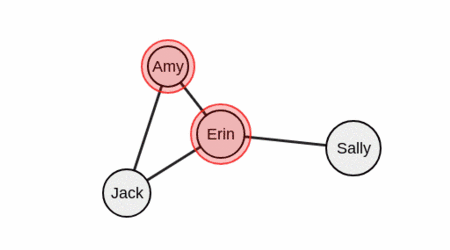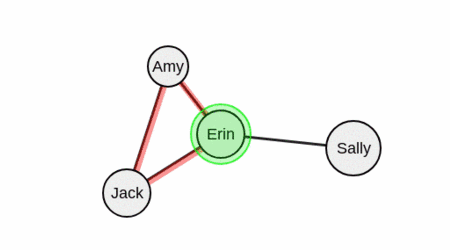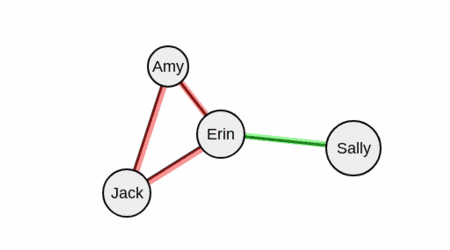
Посмотрите на вершины «Джек», «Эми», «Эрин» и «Сэлли».
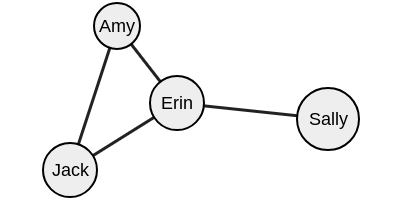
Здесь мы видим две максимальные группы: (1) Эми, Джек и Эрин. (2) Сэлли и Эрин.
Наш мозг обладает большим потенциалом и способен быстро распознать данные группы. Компьютеры тоже имеют высокий потенциал и способны распознать эти группы, если правильно задать параметры.
Какие параметры мы должны задать компьютеру, чтобы он начал видеть то, что видим мы?
Начнем с выбора вершины. Допустим, это будет Джек.
Теперь необходимо запустить рекурсивный вызов на вершину «Джек» и рассмотреть только его соседей.
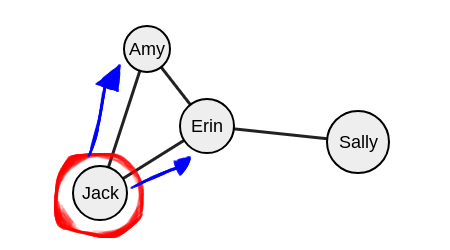
Далее выберите любую из соседних от Джека вершин.
Давайте возьмем вершину «Эми».
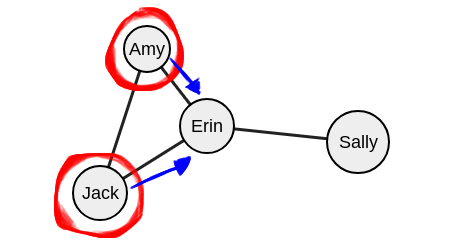
На следующем уровне нужно выбрать вершину, которая принадлежит и множеству соседних вершин для Джека, и множеству соседних вершин для Эми.
Это Эрин.
Для обозначения расположения «принадлежит и множеству соседних вершин для вершины «Джек», и множеству соседних вершин для вершины «Эми» существует термин «пересечение».
На третьем этапе, на уровне вершины «Эрин», пересекающихся соседних вершин нет.
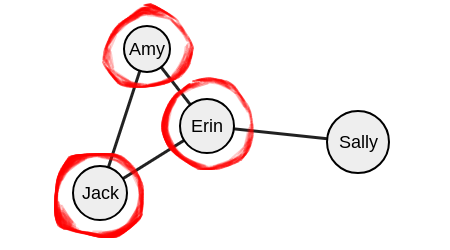
Обратите внимание, что Сэлли не входит в данную группу, так как Сэлли не знакома с Джеком и Эми.
Основной сценарий можно считать верным. Группа найдена.
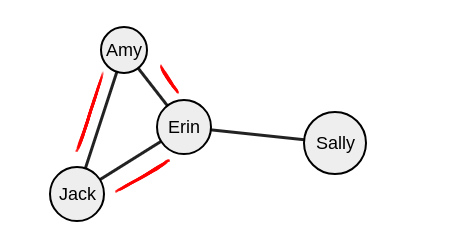
Теперь перейдем к методам поиска с возвратом и исключения.
Поднимемся на один уровень.
Мы нашли максимальную группу в множестве с вершинами «Джек» и «Эми», может, в множестве с вершинами «Джек» и «Эрин».
Выбираем другого соседа Джека — Эрин. Исключаем Эми, и следуем по новому пути.
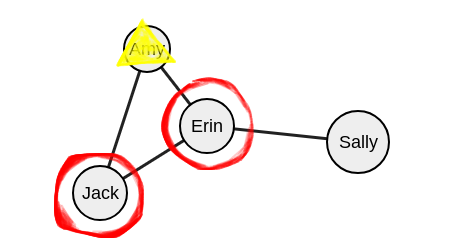
Делаем два рекурсивных вызова, проверяем, нет ли соседних вершин, которые пересекаются с вершинами «Эрин» и «Джек».
В данном случае это Эми, но вершина «Эми» находится в исключенном пересечении.
Основной сценарий в этот раз считается неверным, так как образовать группу с исключенной соседней вершиной невозможно.
Поднимаемся на уровень выше.
Все соседи Джека были просмотрены. Снова поднимаемся на самый высокий уровень.
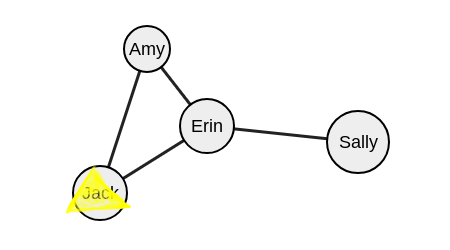
На верхнем уровне исключаем Джека и выбираем любую другую вершину.
Давайте в это раз выберем Эми.
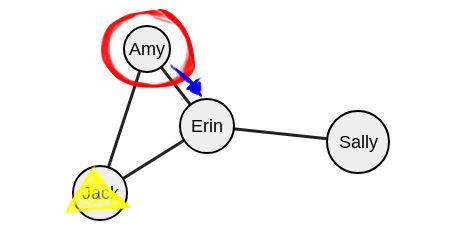
Опустимся на уровень ниже и рассмотрим соседей Эми (которые не были исключены).
Эми знакома с Эрин.
Опустимся ещё на уровень, и проверим, есть ли общие соседи у Эми и Эрин.
Единственной такой вершиной в множестве является вершина «Джек», которая исключена, соответственно тут максимальных групп тоже нет.
Запускаем поиск с возвратом до верхнего уровня.
Эми следует за Джеком (и попадает в множество исключенных вершин), а мы начнем поиск с другой произвольной вершины.
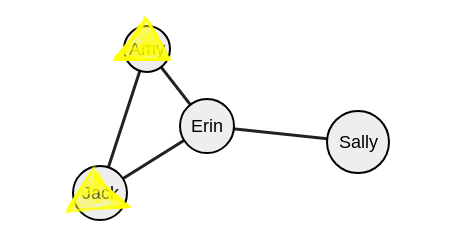
Давайте возьмем вершину «Эрин».
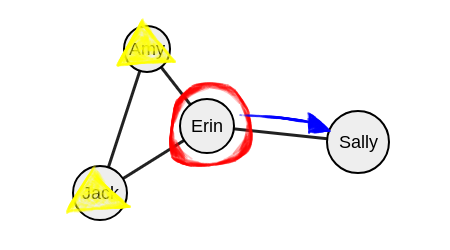
Рассмотрим неисключенных соседей Эрин — это Сэлли.
Вершина выбрана, рекурсия спускается на уровень ниже, поиск продолжается.
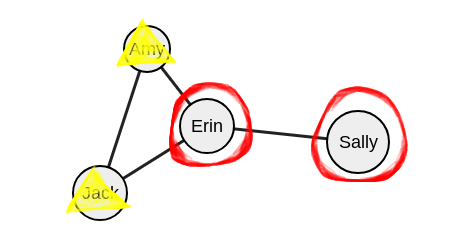
Оцениваем основной сценарий.
(1) Есть ли дополнительные вершины, которые пересекаются с соседними множествами? Нет.
(2) Есть ли вершины, которые входят в число исключенных пересечений с соседними множествами? Нет.
Обратите внимание, что вершина «Сэлли» соединена с «Эрин», а не с Джеком или Эми, и именно по этой причине исключенные вершины «Джек» и «Эми» не входят в это множество пересечений.
Мы нашли группу.
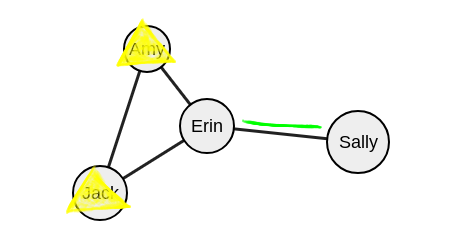
А теперь запускаем поиск с возвратом.
У Эрин больше не осталось вершин, с которыми она могла бы образовать группу, поэтому она следует за Джеком и Эми (и попадает в множество исключенных).
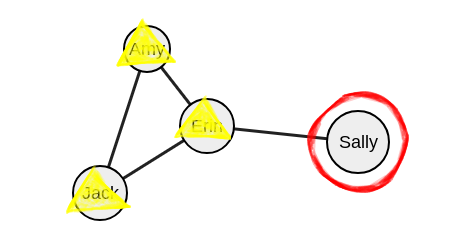
У Сэлли остается только связь с Эрин, а Эрин уже исключена.
Исключаем и Сэлли тоже.
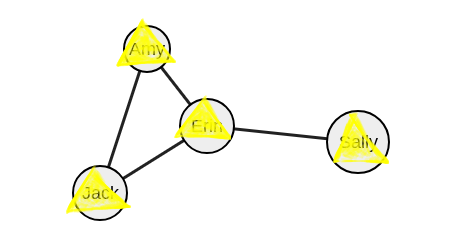
Больше исключать некого. Алгоритм выполнен.
Как это работает
Алгоритм Брона-Кербоша работает на трех множествах: R, P и X.
R := это множество вершин максимальной группы. P := множество возможных вершин максимальной группы. X := множество исключенных вершин.
Алгоритму Брон-Кербоша запускает следующие операции с множествами P, R и X:
R ⋃ {v} := соединение R с единичным множеством (singleton) v.
P ⋂ N(v) := пересечение множества P с соседями v.
X ⋂ N(v) := пересечение множества X с соседями v.
P \ {v} := относительное соотнесение P единичного множества v.
X ⋃ {v} := соединение множества X и единичного набора v.
Псевдокод:
BronKerbosch1(R, P, X):
Если и P, и X окажутся пустыми,
то R — максимальная группа
для каждой вершины v в P:
BronKerbosch1(
R ⋃ {v},
P ⋂ N(v),
X ⋂ N(v)
)
P := P \ {v}
X := X ⋃ {v}
Более подробное описание множеств:
ПРИМЕР СОЕДИНЕНИЯ:
Вершины принадлежат к или к множеству А, или к множеству В.
A = {Джек, Эми}
B = {Джек, Сэлли, Эрин}
A ⋃ B = {Jack, Amy, Sally, Erin}
ПРИМЕР ПЕРЕСЕЧЕНИЯ:
Вершины принадлежат множествам А и B.
A = {Джек, Эми}
B = {Джек, Сэлли, Эрин}
A ⋂ B = {Джек}
ПРИМЕР ОТНОСИТЕЛЬНОГО СООТНЕСЕНИЯ:
Вершины принадлежат множеству А, а не B.
A = {Джек, Эми}
B = {Джек, Сэлли, Эрин}
A \ B = {Эми}
Переведем псевдокод в язык С++:
void bronKerbosch(set<node*> R, set<node*> P, set<node*> X) {
if(P.empty() && X.empty()) {
cout<<"Clique found: ";
set_print(R);
}
set<node*>::iterator v = P.begin();
while(!P.empty() && v!=P.end()){
set<node*> singleton = { (*v) };
bronKerbosch(
set_union(R,singleton),
set_intersection(P,(*v)->friends),
set_intersection(X,(*v)->friends));
P = set_difference(P,singleton);
X = set_union(X,singleton);
if(!P.empty())
v = P.begin();
}
}
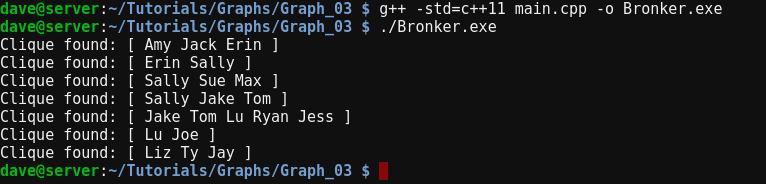
1. Скопируйте код отсюда в текстовый редактор и сохраните как файл main.cpp
2. Составьте в командной строке g++ main.cpp -std=c++11 -o Bronker.exe
3. Потом запустите код из командной строки ./Bronker.exe.
После составления и выполнения исходного кода, программа «организует вечеринку»? и предоставит список всех максимальных групп.
Код
Посмотреть полный код на языке С++ можно здесь.
Перевод статьи David Pynes: Graphs & paths: Bron-Kerbosch, maximal cliques






