Упаковка 2D-прямоугольников в более крупные прямоугольники фиксированного размера необходима в большинстве мультимедийных проектов. В программировании GPU изменение текстур («биндинг») обходится дорого. Таким образом, при рендеринге текста вам не нужно иметь одну текстуру на глиф. Вместо этого желательно упаковать глифы в одну текстуру, называемую «атлас». В 2D-играх атласы, содержащие спрайты, называются листами спрайтов. Листы спрайтов также используются для веб-сайтов, потому что загрузка одного большого файла лучше, чем одного файла на каждую иконку/логотип.
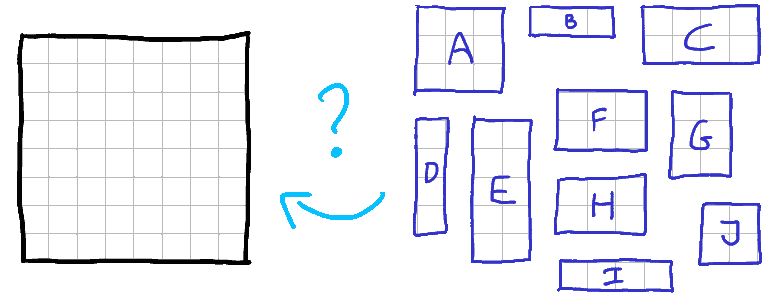
Сначала я думал, что это довольно специфическая проблема, но она также влияет на все отрасли. Сколько объявлений я могу разместить на этой газетной странице? Сколько фигур я могу вырезать на этом куске дерева? Сколько упаковок я могу разместить в задней части фургона доставки? Поэтому задача 2D-упаковки изучалась и в академическом плане.
Самый ценный источник, который я нашел, — отличный обзор от Юкки Юлянки. Он представляет 4 вида алгоритмов и оценивает их на практике. Два из этих алгоритмов выделяются:
MAXRECTS, если вы заранее знаете прямоугольники для упаковки («офлайн-упаковка»);SKYLINE, если вы не знаете («онлайн-упаковка»).
Оффлайн-упаковка оптимальнее, ведь сильно помогает предварительная сортировка прямоугольников. Однако в некоторых случаях сортировка невозможна. В моем сценарии я хочу кэшировать глифы, растеризованные из шрифта, но я заранее не знаю все глифы, которые будут использоваться с каждым шрифтом и каждым форматом (жирный/курсив/размер…).
Вот почему я остановился на алгоритме Skyline. Он также использует stb_rect_pack.h , fontstash и, следовательно, nanovg.
Здесь алгоритм Skyline объясняется и приводится его реализация. Она доступна онлайн (без лицензии).
API, который будет реализован
API, который я предлагаю, автономен, и я старался быть предельно минималистичным. Поэтому API состоит из одной структуры и одной функции. За инициализацию структуры несет тот, кто вызывает код.
struct JvPack2d {
// Массив, способный вместить '2 * maxWidth' uint16_t
uint16_t* pSkyline;
// Размер атласа.
uint16_t maxWidth;
uint16_t maxHeight;
// Закрытое состояние должно быть инициализировано нулями.
bool _bInitialized;
uint16_t _skylineCount;
};
bool jvPack2dAdd(JvPack2d* pP2D, uint16_t const size[2], uint16_t pos[2]);maxWidthи maxHeight прямолинейно просты — это размеры целевого прямоугольника, например, текстуры. Я остановился на координатах с типом uint16_t, ведь я нацелен на текстуры GPU, ограниченные 16384 пикселями на одно измерение.
Массив pSkyline делает пользователя ответственным за распределение. Требуемая емкость 2 * maxWidth — наихудший сценарий, если у вас есть прямоугольники размером в 1 пиксель. Если вы хотите сэкономить несколько килобайтов и знаете (или можете гарантировать), что ширина всех прямоугольников кратна 4, вы можете разделить все ширины и maxWidth на 4 и умножить на 4 горизонтальные позиции, заданные jvPack2dAdd().
Как работает алгоритм Skyline
Алгоритм Skyline упаковывает прямоугольники атласа снизу вверх. Для каждого столбца атласа он отслеживает только самую верхнюю позицию. Концептуально состояние алгоритма эквивалентно одномерной карте высот, смутно напоминающей силуэт зданий, поэтому алгоритм называется Skyline — линия горизонта.
Поскольку алгоритм манипулирует только силуэтом, наложение прямоугольников может создавать не отслеживаемые пробелы, то есть тратить пространство. Это можно смягчить с помощью свободного списка таких пробелов, но подход требует компромисса в производительности.
Затем алгоритм можно разделить на два этапа:
- Следуем за линией горизонта, чтобы найти самую низкую точку, куда можно вставить прямоугольник. Учитывая то же самое вертикальное положение, выбираем самое левое из расположений.
- Обновляем структуру данных горизонта, добавляя силуэт нового прямоугольника.
Структура данных
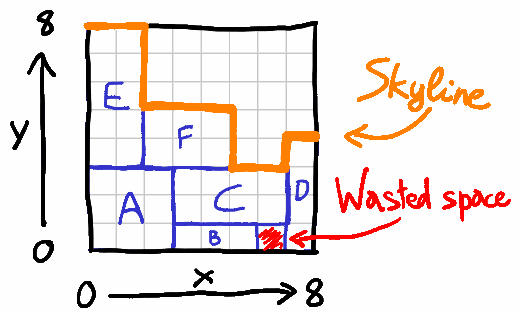
В моей реализации я представляю Skyline как массив координат, каждая координата является левой точкой горизонтального сегмента, отсортированного слева направо. На изображении выше линия горизонта представлена четырьмя точками:
skyline=[(0,8),(2,5),(5,3),(7,4)]В языке C этот массив представлен буфером pSkyline, который по очереди хранит позиции точек по осям X и Y, а также хранит количество точек в буфере: skylineCount. На горизонтальной оси есть пиксели maxWidth, поэтому Skyline может иметь максимум maxWidth сегменты, где каждый сегмент имеет длину в 1 пиксель, например, в форме зубцов замка. Таким образом, массив линии горизонта содержит максимум maxWidth двумерные координаты. Вот почему в API pSkyline должна быть возможность хранить 2 * maxWidth числа.
bool jvPack2dAdd(JvPack2d* pP2D, uint16_t const size[2], uint16_t pos[2])
{
// Нет смысла упаковывать прямоугольники с нулевой шириной и нулевой высотой: выходим сразу.
uint16_t width = size[0];
uint16_t height = size[1];
if (width == 0 || height == 0)
return false;
// Служебная структура, позволяющая сделать индексацию массива более читабельной.
typedef struct Point {
uint16_t x;
uint16_t y;
} Point;
Point* pSkyline = (Point*)pP2D->pSkyline;
// Начальное состояние содержит левую нижнюю точку.
if (!pP2D->_bInitialized) {
_jvASSERT(pP2D->maxWidth, >, 0);
_jvASSERT(pP2D->maxHeight, >, 0);
pP2D->_bInitialized = true;
pP2D->_skylineCount = 1;
pSkyline[0].x = 0;
pSkyline[0].y = 0;
}Поиск места вставки
Чтобы найти лучшее место для кандидата, алгоритм проходит по горизонту, то есть по нижней строке, затем по самому левому столбцу. Ему не нужно проходить по каждому столбцу. Он проходит только по каждой точке массива горизонта, поскольку предпочитает «самый левый столбец»: если найдена другая подходящая позиция, лучшая позиция получается ее перемещением влево, пока не достигается одна из закодированных точек.
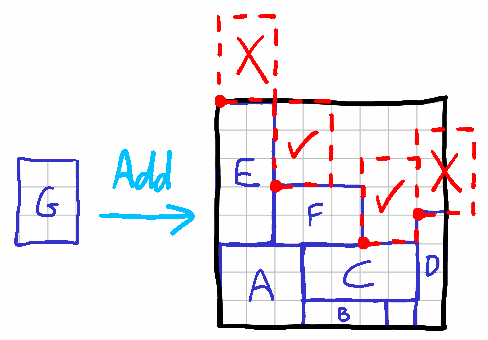
Дан прямоугольник размером (w,h), мы стараемся подходить под каждую позицию кандидата (х,у). Находим, какие точки горизонта ( х2,у2) горизонтально перекрываются прямоугольником, т. е. х≤х2<x+w. Это делается по двум причинам:
- Если у2>у, прямоугольник сталкивается с линией горизонта. Тогда этот прямоугольник поднимается вверх, чтобы предотвратить столкновение у←у2.
- Эти перекрывающиеся точки удалятся из массива линии горизонта, поскольку они будут затенены силуэтом нового прямоугольника.
Диапазон перекрывающихся точек для лучшего кандидата в коде сейчас хранится как два индекса: idxBest (включительно) и idxBest2 (не включительно). Эти перекрывающиеся точки — всегда последовательный диапазон, поскольку массив отсортирован по возрастанию горизонтальной позиции.
// Алиасы, чтобы сделать код не таким многословным.
uint16_t maxWidth = pP2D->maxWidth;
uint16_t maxHeight = pP2D->maxHeight;
uint16_t skylineCount = pP2D->_skylineCount;
// Хранит лучшего на текущий момент кандидата
uint16_t idxBest = UINT16_MAX;
uint16_t idxBest2 = UINT16_MAX;
uint16_t bestX = UINT16_MAX;
uint16_t bestY = UINT16_MAX;
// Цикл поиска лучшего расположения.
for (uint16_t idx = 0; idx < skylineCount; ++idx) {
uint16_t x = pSkyline[idx].x;
uint16_t y = pSkyline[idx].y;
if (width > maxWidth - x)
break; // Мы достигли правой границы атласа.
if (y >= bestY)
continue; // Текушее лучшее расположение не найдено.
// Поднимает y так, чтобы мы оказались над всеми точками пересечения.
uint16_t xMax = x + width;
uint16_t idx2;
for (idx2 = idx + 1; idx2 < skylineCount; ++idx2) {
if (xMax <= pSkyline[idx2].x)
break; // Мы не доходим до следующих точек.
if (y < pSkyline[idx2].y)
y = pSkyline[idx2].y; // Поднимает 'y' так, чтобы не пересекался.
}
if (y >= bestY)
continue; // Мы не достигли текущего лучшего расположения.
if (height > maxHeight - y)
continue; // Мы достигли верхней границы атласа.
idxBest = idx;
idxBest2 = idx2;
bestX = x;
bestY = y;
}
if (idxBest == UINT16_MAX)
return false; // Не нашлось свободного пространства.
_jvASSERT(idxBest, <, idxBest2);
_jvASSERT(idxBest2, >, 0);Обновление структуры данных Skyline
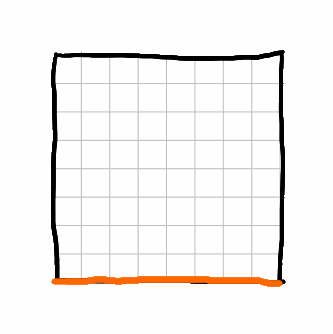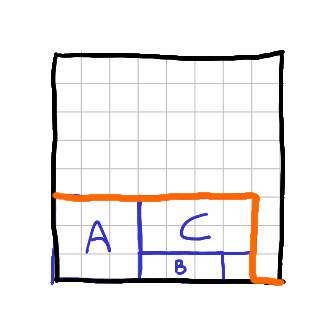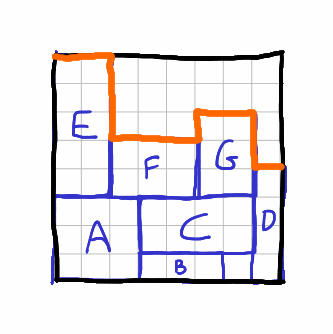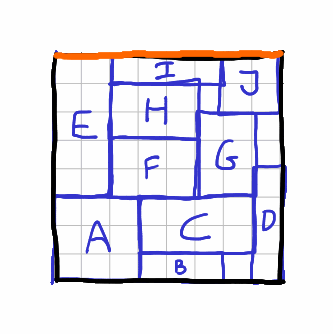
После того как мы нашли наилучшее положение, нам нужно обновить массив Skyline. Перекрывающиеся точки, определенные на предыдущих шагах, удаляются и заменяются одной или двумя точками, соответствующими силуэту добавленного прямоугольника. На следующем изображении показываются три возможных случая.
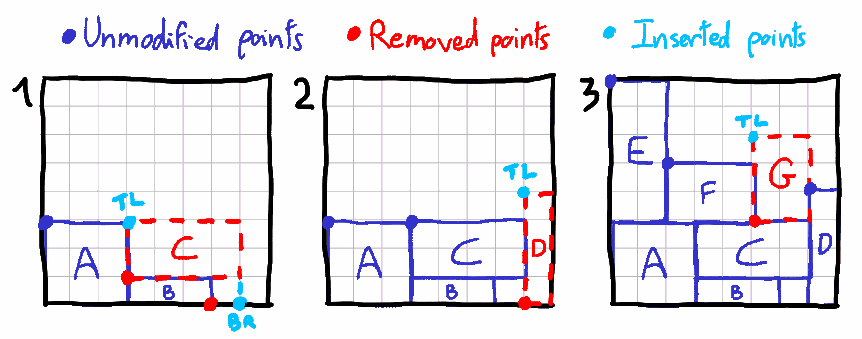
- Новый прямоугольник C перекрывает две точки, которые будут удалены. Добавляются две точки: TL сверху слева и BR — снизу справа. Обратите внимание, что BR опускается на ту же строку, что и последняя перекрывающаяся точка.
- Новый прямоугольник D перекрывает одну позицию, которая будет удалена — это начало координат прямоугольника. Добавляется верхняя левая точка TL. Нижняя правая точка BR не добавляется: она будет соответствовать правой границе атласа.
- Новый прямоугольник G перекрывает одну удаляемую позицию — начало координат прямоугольника. Добавляется верхняя левая точка TL. Нижняя правая точка BR не добавляется: она будет соответствовать тому же столбцу, что и следующая точка в массиве Skyline, а мы хотим сохранить не более одной точки на столбец, чтобы гарантировать производительность и использование памяти для худшего случая.
Решение соответствует следующему коду.
// Заменяем точки, заслоненные текущим прямоугольником, новыми точками.
uint16_t removedCount = idxBest2 - idxBest;
Point newTL, newBR; // TopLeft, BottomRight
newTL.x = bestX;
newTL.y = bestY + height;
newBR.x = bestX + width;
newBR.y = pSkyline[idxBest2 - 1].y;
bool bBottomRightPoint =
(idxBest2 < skylineCount ? newBR.x < pSkyline[idxBest2].x : newBR.x < maxWidth);
// TopLeft вставляется всегда
uint16_t insertedCount = 1 + bBottomRightPoint;
_jvASSERT(skylineCount + insertedCount - removedCount, <=, maxWidth);Затем нам нужно либо сжать, либо расширить массив, чтобы обеспечить удаление и вставку. Со стандартной библиотекой, предоставляющей утилиты для работы с массивами, например std::vector из C++, это может быть просто один вызов .erase(), затем .insert(). Но для этой статьи я предпочитаю выразить алгоритм независимо от стандартной библиотеки, поэтому реализация сдвигает элементы явно:
// Логика для вставки и стирания в массиве.
// Это можно сделать в две строки, если использовать стандартную библиотеку,
// например, в C++ это будут std::vector erase() + insert(),
// но я предпочитаю, чтобы алгоритм был явным и независимым.
if (insertedCount > removedCount) {
// Расширение. Сдвигаем элементы вправо. Итерировать нужно назад.
uint16_t idx = skylineCount - 1;
uint16_t idx2 = idx + (insertedCount - removedCount);
for (; idx >= idxBest2; --idx, --idx2)
pSkyline[idx2] = pSkyline[idx];
pP2D->_skylineCount = skylineCount + (insertedCount - removedCount);
}
else if (insertedCount < removedCount) {
// Сжатие. Сдвигаем элементы влево Итерировать нужно вперед.
uint16_t idx = idxBest2;
uint16_t idx2 = idx - (removedCount - insertedCount);
for (; idx < skylineCount; ++idx, ++idx2)
pSkyline[idx2] = pSkyline[idx];
pP2D->_skylineCount = skylineCount - (removedCount - insertedCount);
}
pSkyline[idxBest] = newTL;
if (bBottomRightPoint)
pSkyline[idxBest + 1] = newBR;
pos[0] = bestX;
pos[1] = bestY;
return true;
}Результаты
Вот GIF-анимация, показывающая, как алгоритм Skyline решает исходную задачу:
Что касается производительности, у меня нет надлежащего бенчмарка, но в рамках моих модульных тестов я написал четыре сценария «худшего случая», где атлас заполняется различными узорами, и получить время их выполнения было довольно легко. Технически код также проверяет утверждения, но после профилирования кода утверждения не были частью горячего пути выполнения кода, поэтому измерение кажется репрезентативным. Сценарии параметризованы единственным параметром ATLAS_SIZE.
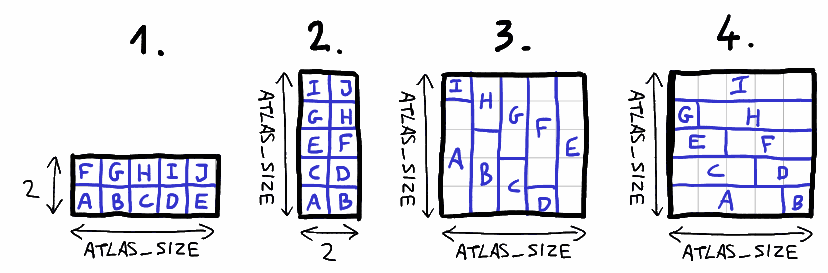
WorstCaseWidth— размер атласа(ATLAS_SIZE, 2), и вставляются прямоугольники размером(1,1). Прямоугольники2 * ATLAS_SIZEупакованы. Требуется4 * ATLAS_SIZEбайтов.WorstCaseHeight— размер атласа(2, ATLAS_SIZE), вставляются прямоугольники размером(1,1). Прямоугольики2 * ATLAS_SIZEупакованы. Требуется8байтов.WorstCaseDiagonalVertical— размер атласа составляет(ATLAS_SIZE, ATLAS_SIZE). Чтобы сформировать диагональный узор, вставляются прямоугольники шириной 1. Прямоугольники2 * ATLAS_SIZE - 1упакованы. Требуется4 * ATLAS_SIZEбайтов.WorstCaseDiagonalHorizontal— размер атласа составляет(ATLAS_SIZE, ATLAS_SIZE). Чтобы сформировать диагональный узор, вставляются прямоугольники высотой 1. Прямоугольники2 * ATLAS_SIZE - 1упакованы. Требуется4 * ATLAS_SIZEбайтов.
Вот сравнение времени выполнения соответствующего модульного теста. В каждой строке ATLAS_SIZE удваивается, поэтому также удваивается количество упакованных прямоугольников. Измерение проводилось на ноутбуке с процессором AMD Ryzen 5 7520U 2.80 GHz, а значит, сырое время не так важно, но динамика ATLAS_SIZE интересна.
| ATLAS_SIZE | WorstCaseWidth | WorstCaseHeight | WorstCaseDiagonalVertical | WorstCaseDiagonalHorizontal |
|---|---|---|---|---|
| 512 | 0,7 мс | 0,0 мс | 0,6 мс | 0,0 мс |
| 1024 | 2,9 мс | 0,0 мс | 3,0 мс | 0,0 мс |
| 2048 | 10,0 мс | 0,0 мс | 10,2 мс | 0,0 мс |
| 4096 | 37,2 мс | 0,1 мс | 39,8 мс | 0,2 мс |
| 8192 | 122,3 мс | 0,2 мс | 166,7 мс | 0,4 мс |
| 16384 | 524,4 мс | 0,6 мс | 775,2 мс | 0,6 мс |
| 32768 | 2322,1 мс | 1,1 мс | 2355,7 мс | 1,1 мс |
| 65535 | 7935,0 мс | 2,4 мс | 9549,4 мс | 1,9 мс |
WorstCaseHeightиWorstCaseDiagonalHorizontalсостоят из двух прямоугольников на строку. Время вставки вATLAS_SIZEкороткое и линейное. Стоимость каждого добавленного прямоугольника фиксирована.WorstCaseWidthиWorstCaseDiagonalVerticalсостоят из двух прямоугольников на столбец. Время вставки намного дольше, оно квадратично поATLAS_SIZE. Стоимость каждого добавленного прямоугольника сама по себе линейна поATLAS_SIZE.
Обратите внимание, что алгоритм содержит два вложенных цикла, поэтому стоимость каждого добавленного прямоугольника теоретически может быть квадратичной по ATLAS_SIZE, но я не измерял ее. Интуитивно без математического анализа я понимаю, что внутренний цикл проверки столкновений с линией горизонта пропорционален ширине прямоугольника. Но чем больше ширина, тем меньше точек будет на линии горизонта, поэтому внешний цикл в следующий раз выполняет меньше работы.
Реализация доступна и открыта без лицензии.
Читайте также:
- 7 React-проектов, которые помогут вам стать лучшим разработчиком
- 70% интервьюеров задают эти 5 вопросов по React.js
- Топ-25 полезных советов для React-разработчиков. Часть 2
Читайте нас в Telegram, VK и Дзен
Перевод статьи Julien Vernay: Skyline algorithm for packing 2D rectangles






