Данные и алгоритмы находятся в центре внимания специалиста по науке о данных. Понимание данных помогает ему принимать приоритетные решения, а понимание алгоритмов — моделировать данные в соответствии с точными расчетами. Линейная регрессия считается отправным пунктом, с которого новички в области науки о данных приступают к моделированию данных.
Цель этой статьи — дать представление об алгоритме линейной регрессии, его реализации на языке программирования Python и практическом применении. Для начала выясним, что такое алгоритм линейной регрессии.
Что такое линейная регрессия?
Линейная регрессия — это алгоритм машинного обучения, который в основном используется для проведения регрессионного анализа. Хотя на регрессионный анализ настроено множество моделей, все они являются оптимизированными версиями двух базовых регрессионных моделей — простой линейной регрессии и множественной линейной регрессии.
Несмотря на то, что регрессионный анализ можно рассматривать и с точки зрения статистики, он, как и другие модели МО, нацелен на минимизацию ошибок. Линейная регрессия использует только линейную функцию, помогая в моделировании взаимосвязи между зависимыми и независимыми переменными.
Стоит отметить, что модели линейной регрессии давно и активно используются в анализе данных, в частности в одном из ведущих его разделов — анализе временных рядов. Посмотрим, как работают эти модели.
Как работает линейная регрессия?
Регрессионный анализ осуществляется путем оценки коэффициента линейного уравнения. При этом может быть одна или несколько независимых переменных, которые коррелируют и лучше всех подходят для прогнозирования значения зависимой переменной.
Можно считать, что регрессионный анализ выполняется путем подгонки прямой линии к данным, которые стремятся к уменьшению расхождения между фактическими и прогнозируемыми значениями зависимой переменной.
Из множества методов обучения линейных регрессионных моделей по данным наиболее распространенным является метод наименьших квадратов. Он также называется регрессией наименьших квадратов. Попробуем разобраться в линейной регрессии на примере данных о росте и весе учеников в классе.
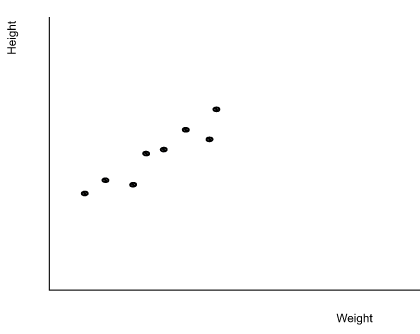
Будем исходить из того, что с увеличением роста ученика увеличивается и его вес. Нанесение этих данных между двумя координатами будет выглядеть следующим образом:
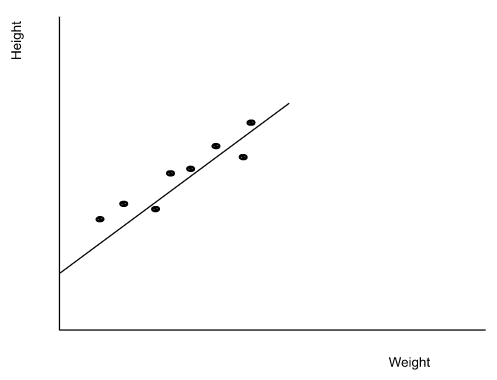
Изучив эти данные, регрессионная модель может предсказать рост ученика по его весу. Это процесс нахождения простой линейной зависимости между весом и ростом.
Математически такая линейная зависимость выражается следующим образом:
Y = mx + c
Это простое линейное уравнение, которое позволяет предсказать значение y (рост) по заданному значению x (вес). Построить линию с помощью этого уравнения можно путем нахождения значений m (коэффициент) и c (точка пересечения с осью y).
После нахождения всех значений и построения соответствующих линий модель готова к использованию для прогноза. В качестве результата модель выдаст значение y. Перед началом моделирования данных с помощью модели линейной регрессии необходимо рассмотреть некоторые допущения, связанные с этой моделью.
Допущения
С работой любой линейной регрессионной модели принято связывать четыре основных допущения.
- Линейность. Между средним значением зависимой переменной и независимыми переменными должна существовать линейная связь. Эта связь измеряется путем выявления изменений зависимой переменной в связи с изменениями независимых переменных.
- Гомоскедастичность. В линейной регрессии гомоскедастичность имеет важное значение, поскольку представляет собой степень подгонки модели под данные. Она определяет дисперсию по величине погрешности или остатков: если дисперсия увеличивается, значит модель подогнана плохо.
- Независимость. Собранные точки данных должны быть независимы друг от друга.
- Нормальность. Должно быть нормальное распределение для любого из фиксированных значений зависимой и независимой переменных.
Это были основные допущения, принимаемые во внимание при моделировании данных с помощью модели линейной регрессии. Теперь перейдем к рассмотрению реализации модели простой линейной регрессии.
Реализация
Регрессионные модели могут быть реализованы с помощью различных инструментов, таких как R, Python, MATLAB и Excel. В этой статье будет использован язык программирования Python и его библиотека Sklearn, которая предоставляет функции для реализации различных регрессионных моделей в пакете Linear_model. Весь список функций для регрессионных моделей можно найти здесь. Начнем с импорта и подготовки данных.
Подготовка данных
Чтобы избавиться от таких процессов, как EDA, валидация данных и т. д., будем использовать предоставленный Sklearn набор данных “Diabetes” (“Диабет”). Это позволит сразу перейти от загрузки данных к их разбиению.
from sklearn.datasets import load_diabetes
var_X, var_y = load_diabetes(return_X_y=True)
print(“number of independent variables:”, var_X.shape[1:])
print(“number of data points:”, var_y.shape)Вывод:

Как видите, в этом наборе данных 10 независимых переменных и 442 точки данных. Для оптимизации процесса можно выбрать только одну независимую переменную, чтобы применить к данным простую линейную регрессионную модель.
import numpy as np
var_X = var_X[:, np.newaxis, 2]
var_X.shapeВывод:
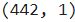
Теперь необходимо разделить набор данных для обучения и тестирования регрессионной модели.
from sklearn.model_selection import train_test_split
X_train, X_actual, y_train, y_actual = train_test_split(
var_X, var_y, test_size=0.10, random_state=42)
print(“number of data points in training data”, X_train.shape, X_train.shape)
print(“number of data points in testing data”, X_actual.shape, y_actual.shape)Вывод:

Как видите, сформированы разделенные наборы данных — для обучения и для тестирования. Теперь можно импортировать и обучать модель, используя обучающие наборы данных.
Моделирование
Импортирование модели:
from sklearn.linear_model import LinearRegression
LineR = LinearRegression()Теперь можно подогнать модель для прогнозирования значений на основе данных.
LineR.fit(X_train, y_train)
predictions = LineR.predict(X_actual)Прежде чем увидеть, что предсказала модель, визуализируем тестовые данные.
import matplotlib.pyplot as plt
plt.scatter(X_actual, y_actual)Вывод:
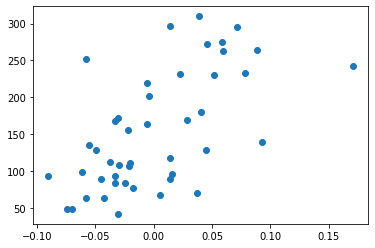
На приведенной выше визуализации виден разброс данных между координатами, а теперь посмотрим на предсказанные моделью значения.
plt.scatter(X_actual, y_actual)
plt.plot(X_actual, prediction,linewidth=6)Вывод:
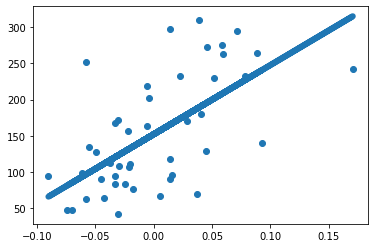
Здесь можно увидеть, как работала модель для составления прогнозов. Теперь, имея представление о реализации простой регрессионной модели, перейдем к изучению оценочных метрик, которые используются для оптимизации работы модели.
Метрики оценки
Оценка любой модели машинного обучения — важнейшая задача, сопутствующая моделированию данных. Кроме того, некоторые метрики помогают оценить саму подогнанную модель. В этой статье будут представлены официально принятые метрики оценки модели линейной регрессии. Познакомьтесь с их интерпретациями.
1. MAE (mean absolute error, средняя абсолютная ошибка) — это универсальная метрика, которая позволяет узнать разницу между фактическими и прогнозируемыми значениями. Она рассчитывается по следующей формуле:
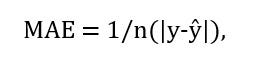
где
- n = количество точек данных;
- y = фактический выход;
- Ŷ = прогнозируемый выход.
2. MSE (mean squared error, средняя квадратичная ошибка) можно рассматривать как уточненную MAE, поскольку она помогает находить ошибки с помощью квадратичной разницы между фактическими и прогнозируемыми значениями. Ниже приведена формула, которую используют для вычисления этой метрики:
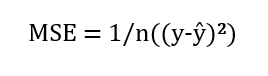
3. RMSE (root mean squared error, корень квадратный из средней квадратичной ошибки) также показывает разницу между фактическими и прогнозируемыми значениями, извлекая корень квадратный из средней квадратичной ошибки.
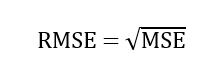
4. RMSLE (root mean squared logarithmic error, корень квадратный из средней квадратичной логарифмической ошибки) использует логарифмически преобразованные прогнозируемые и фактические значения, проверяемые по корню квадратному из средней квадратичной ошибки. Чтобы избежать натурального логарифма нуля, в оба вида значений добавляется 1. Для оценки моделей применяется следующая формула этой метрики:
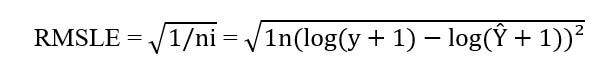
5. R² (R-squared, R-квадрат) также считается универсальной метрикой, применяемой для оценки эффективности регрессионной модели. R-квадрат получают путем определения доли вариаций зависимой переменной, что прогнозируется по независимой переменной. Рассчитывается эта метрика по следующей формуле:
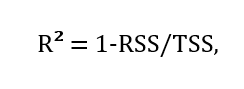
где
- R² = коэффициент детерминации;
- RSS (root of sum of squares) = остаточная сумма квадратов;
- TSS (total sum of squares) = полная сумма квадратов.
6. Adjusted R² (скорректированный R²) необходим, когда в данные добавляются новые признаки. Эта метрика компенсирует недостатки R-квадрата, которые уменьшаются или увеличиваются при увеличении дисперсии признаков. Данная метрика рассчитывается по формуле:
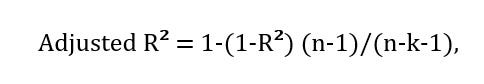
где
k = количество независимых переменных.
Все перечисленные метрики используются для оценки моделей. Библиотека Sklearn предоставляет модули для этих оценочных метрик, которые можно найти здесь. Теперь перейдем к вопросу о применении регрессионных моделей.
Применение линейной регрессии
На практике линейная регрессия используется в самых различных сферах. Условно их можно разделить на две основные категории.
- Прогнозирование. Если необходимо сделать прогноз на основе прошлых данных, а зависимые и независимые переменные имеют линейную корреляцию, используют модель линейной регрессии. К этой категории можно отнести прогнозирование ситуации на фондовом рынке, прогноз погоды, прогнозирование продаж и т. д.
- Оптимизация прочности связей. Иногда при анализе данных может потребоваться узнать тип связи и силу связи двух или более переменных. В таких ситуациях используют линейную регрессию, которая помогает понять, как изменится данная переменная при изменении других переменных. Оптимизация прочности связи находит применение в медицине, розничной торговле, сельском хозяйстве.
Заключение
В данной статье были изложены базовые понятия, касающиеся линейного регрессионного моделировании и его реализации с помощью языка программирования Python. Эта тема науки о данных связана с контролируемыми данными, где зависимые переменные являются непрерывными и зависят от независимой переменной. Ниже перечислены практические шаги, которые рекомендуется сделать после прочтения этой статьи.
- Проверка корректности допущений.
- Оценка модели.
- Нахождение коэффициента.
- Определение ошибки.
- Использование множественной линейной регрессии.
Здесь можно найти фрагменты кода из статьи.
Читайте также:
- Как использовать MSE в науке о данных
- 3 случая, когда линейная модель может ошибаться
- ТОП-4 официальных сайта МО-библиотек и способы их использования
Читайте нас в Telegram, VK и Дзен
Перевод статьи Data Science Wizards: Getting started with machine learning algorithms: Linear Regression





