“Мир полон волшебных вещей, терпеливо ожидающих того момента, когда наши чувства станут острее”. — У.Б. Йейтс
Что стоит за #(хэштегом)?
Совсем недавно я начала новую серию статей, смысл которых выражен хэштегом: #TheNotSoToughML (#НисколькоНеСложноеМО).
Предыдущие части: Часть 1, Часть 2.
Мне хотелось бы дать вам упрощенные решения некоторых проблем, возникающих в связи с алгоритмами/концепциями. Вместо того, чтобы сразу вдаваться в математику, я обращаюсь к вашей интуиции. Поверьте: машинное обучение вовсе не сложно. Оно больше похоже на интуитивное постижение, проверяемое алгоритмически.
Концепция 1: Функция ошибки. Измерение результатов
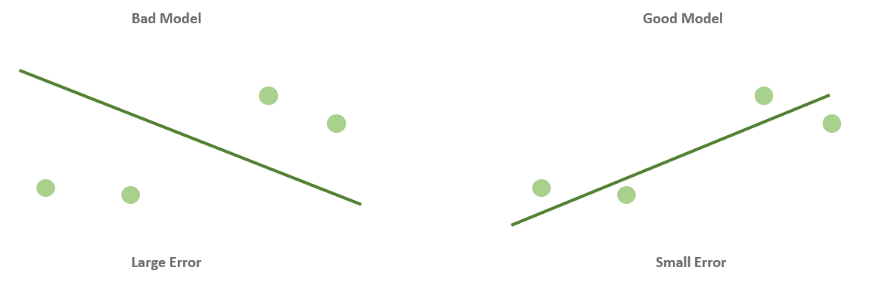
Когда вы смотрите на две модели выше и сравниваете их, приходите ли вы к тому же выводу, что и я? Как по-вашему, является ли плохая модель действительно “плохой” по сравнению с моделью справа? Если да, это значит, что вы сконцентрировали внимание на “зазоре” или расстоянии линии от каждой точки данных; таким образом, в среднем (или по совокупности признаков) вам показалось, что модель слева имеет большее расстояние между точками и линией по сравнению с моделью справа.
Функция ошибки помогает нам понять то же самое! Это метрика, показывающая то, как работает наша модель.
Функция ошибки будет присваивать большее значение модели слева и меньшее — модели справа. В специальной литературе такие функции также называют функциями потерь или функциями затрат.
Теперь перейдем к более важному вопросу.
Как определить, насколько точно работает функция ошибки для моделей линейной регрессии?
Сейчас мы поговорим об абсолютной ошибке и квадратичной ошибке.
Абсолютная ошибка — метрика, которая складывает расстояния и показывает, насколько хороша наша модель.
Это самый простой для понимания и интерпретации показатель.
Это просто суммирование расстояний между точками данных и линией. Оно называется “абсолютным”, потому что расстояние может быть положительным или отрицательным в зависимости от расположения точек данных по отношению к линии. Следовательно, чтобы не упустить ни одного нюанса в поведении модели, мы принимаем абсолютное значение ошибок.
Итак, мы знаем, что хорошая модель линейной регрессии — это та модель, в которой линия близка к точкам данных.
Но что значит “близка”?
Выбираем ли мы линию, которая близка к некоторым точкам и далека от других? Или мы выбираем линию, которая близка ко всем точкам?
Вот тут-то и пригодится функция абсолютной ошибки. Мы выбираем линию, которая минимизирует абсолютную ошибку, т.е. ту, для которой сумма вертикальных расстояний от каждой точки до линии минимальна.
На рисунке ниже показаны разные абсолютные ошибки.
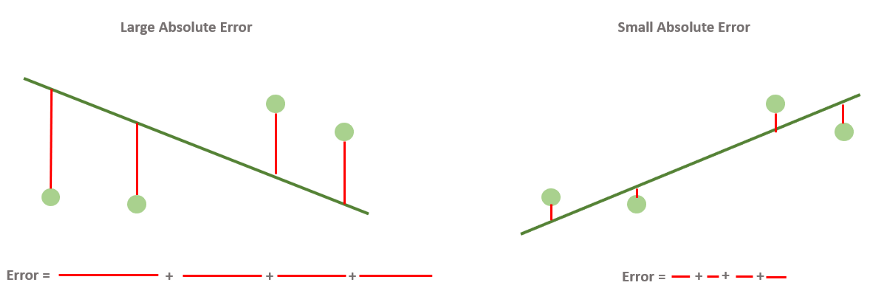
Теперь перейдем к следующему приему, связанному с ошибками.
Квадратичная ошибка — метрика, которая складывает квадраты расстояний и показывает, насколько хороша наша модель.
Квадратичная ошибка очень похожа на абсолютную ошибку. Но теперь, вместо того, чтобы брать абсолютное значение разницы между меткой и прогнозированной меткой, мы используем квадрат, что снова превращает число в положительное.
Давайте попробуем представить это так же, как мы это делали для абсолютной ошибки!
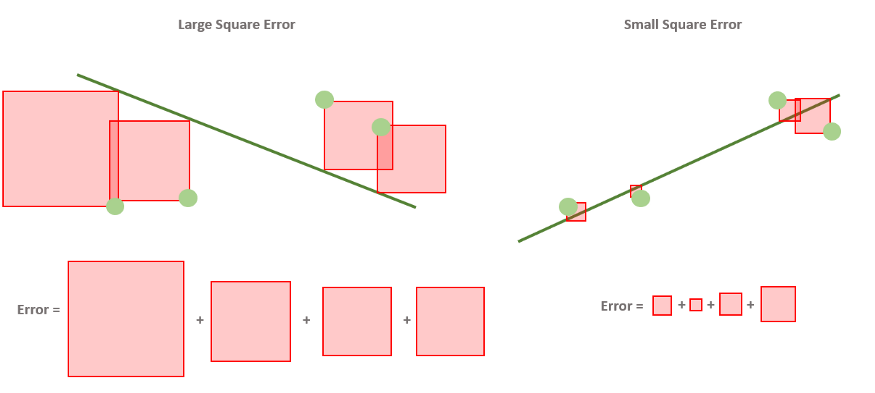
Квадратичная ошибка используется на практике чаще, чем абсолютная. Почему? Одна из причин заключается в том, что у квадрата гораздо более наглядная производная, чем у абсолютного значения, что очень удобно в процессе обучения.
Мы убедимся в этом чуть ниже.
Средняя абсолютная ошибка и (корневая) средняя квадратичная ошибка — самые распространенные и наиболее полезные ошибки для нашей модели
Абсолютная и квадратичная ошибки, показанные выше, служили простыми примерами того, что такое ошибки и как они могут выглядеть. Однако наиболее часто используемыми ошибками в проектах машинного обучения, особенно когда мы имеем дело с регрессионными моделями, являются средняя абсолютная ошибка (MAE) и средняя квадратичная ошибка (MSE).
Они определяются практически так же, только вместо вычисления сумм мы вычисляем средние значения.
Итак, MAE — это среднее значение вертикальных расстояний от точек до линии, а MSE — среднее значение квадратов этих же расстояний.
Эти ошибки более полезны, чем абсолютная и квадратичная ошибка, которые мы вычисляли в предыдущем разделе, и вот почему. Допустим, мы пытаемся подогнать одну и ту же модель к двум разным наборам данных, в одном из которых всего 10 точек данных, а в другом — миллион. Если ошибка является суммой величин (как в случае абсолютной или квадратичной ошибки), то она, вероятно, будет намного выше в наборе данных, состоящем из миллиона точек, потому что мы будем складывать гораздо больше чисел. Но эта проблема решается с помощью средних значений.
Еще один полезный показатель — среднеквадратичная ошибка (RMSE). Как следует из названия, это корень из средней квадратичной ошибки. Этот показатель используется для сопоставления единиц в задаче, а также для того, чтобы дать нам лучшее представление о том, насколько сильно модель ошибается при прогнозировании.
Концепция 2: Градиентный спуск. Уменьшение функции ошибки путем медленного “спуска с горы”
Теперь поговорим о перемещении линий на некоторое расстояние в контексте МО.
Поскольку цель этого цикла — объяснить интуитивный подход, а математические понятия использовать только там, где это абсолютно необходимо, мы воздержимся от того, чтобы углубляться в технические аспекты в этом разделе. Но если вы хотите разобраться в расчетах, которые проводятся при градиентном спуске, можете зайти на этот сайт и ознакомиться с ними.
Пока же мы попробуем понять, как градиентный спуск помогает нам уменьшить ошибку модели. При этом постараемся не погружаться в высшую математику. Скромная попытка, но все же.
Давайте решим вышеуказанную задачу в следующем порядке:
- Кратко разберем, как работает градиентный спуск.
- Расскажем, как он может решить задачу уменьшения ошибки
- Выясним, как с помощью полученных знаний мы узнаем, когда нужно останавливать работу алгоритма.
Как работает градиентный спуск
Представьте, что вы находитесь на вершине высокой горы — скажем, горы “Эррорест”.
Вы хотите спуститься с нее, но стоит очень туманная погода и вы видите только на расстоянии около 1 метра от себя. Что же делать? Вот вам дельный совет — оглянитесь вокруг себя и определите, в каком направлении можно сделать один единственный шаг так, чтобы спуститься максимально низко.
Нашли это направление? Теперь сделайте маленький шаг. Поскольку этот шаг был сделан в направлении максимального спуска, то, скорее всего, вы спуститесь на небольшое расстояние.
Теперь вам нужно повторять это действие много раз до тех пор, пока вы не достигнете подножия горы (хотелось бы надеяться на это).
Я написал “хотелось бы надеяться”, потому что в этом примере слишком много нюансов, которые мы разбирать не будем, чтобы не вдаваться в сложные математические понятия. Вы можете достичь подножия горы, а можете очутиться в долине, и вам больше некуда будет идти. Сейчас мы не станем разбирать все эти варианты.
Суть в том, что при градиентном спуске мы делаем один шаг за раз в направлении самой низкой точки (в нашем примере — подножия горы).
Как градиентный спуск помогает решить задачу уменьшения ошибки
Напомню, что мы определяем алгоритм линейной регрессии по следующей схеме:
- Начинаем с любой линии.
- Находим наилучшее направление, в котором можно немного сдвинуть нашу линию, используя прием из сферы абсолютных или квадратичных значений.
- Перемещаем линию в этом направлении.
- Повторяем эти шаги 2, 3 и более раз.
В предыдущем разделе мы говорили о градиентном спуске. Чтобы закрепить принцип его работы с помощью примера с горой, пройдем описанные этапы еще раз:
- Мы находимся на вершине горы.
- Находим оптимальное направление для первого маленького шага.
- Делаем маленький шаг в этом направлении.
- Повторяем эти шаги 2, 3 и более раз.
Знакомая схема, не так ли? Посмотрим на рисунок ниже.
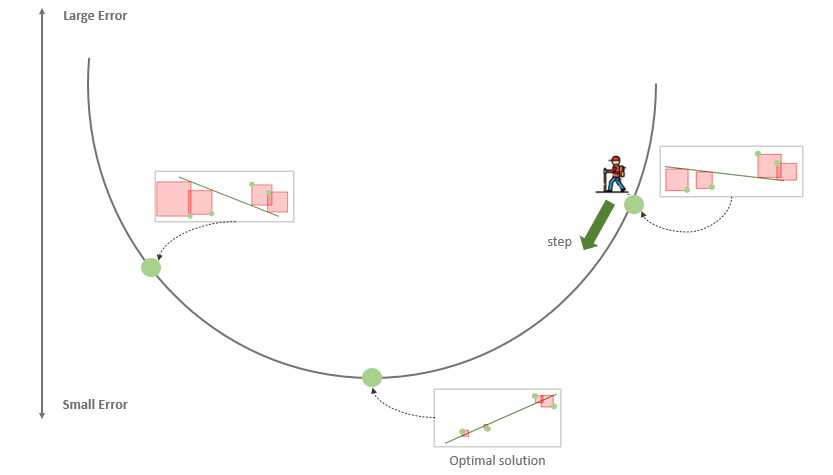
Единственное отличие от нашего прежнего понимания линейной регрессии заключается в том, что эта функция ошибки больше напоминает долину, чем гору. Наша цель — спуститься в самую низкую точку. Каждая точка в этой долине соответствует некоторой модели (линии), которая пытается подогнать наши данные. Высота точки — это ошибка, которую выдает данная модель. Таким образом, плохие модели располагаются сверху, а хорошие — снизу. Мы стараемся опуститься как можно ниже. Каждый шаг ведет нас от худшей модели к чуть лучшей. Если мы будем делать такие шаги много раз, то в конце концов дойдем до лучшей модели (или, по крайней мере, довольно хорошей!).
Подытожим: что же нам нужно делать?
Мы хотим найти линию, которая лучше всего соответствует нашим данным. У нас есть метрика “функция ошибки”, которая показывает, насколько линия далека от данных. Таким образом, если мы сможем уменьшить это число как можно больше, мы найдем наиболее подходящую линию.
Этот процесс часто используется во многих областях математики и называется минимизацией функций (т.е. нахождение наименьшего возможного значения, которое может вернуть функция). В данном случае функция, которую мы пытаемся минимизировать, — это ошибка (абсолютная или квадратичная) нашей модели. Для минимизации этой функции мы используем градиентный спуск.
Как узнать, когда нужно останавливать работу алгоритма?
Давайте рассчитаем RMSE для любого набора данных, где мы пытаемся предсказать неизвестные значения (“метки”) и получить новые метки после запуска нашей модели (“прогнозы”):
def rmse(labels, predictions):
n = len(labels)
differences = np.subtract(labels, predictions)
return np.sqrt(1.0/n * (np.dot(differences, differences)))
Теперь построим график, отобразив на нем, помимо прочего, количество эпох (итераций), в течение которых работает ваша модель. В итоге вы получите результат, похожий на тот, который вышел у меня, когда я тестировал таким образом свой образец набора данных:
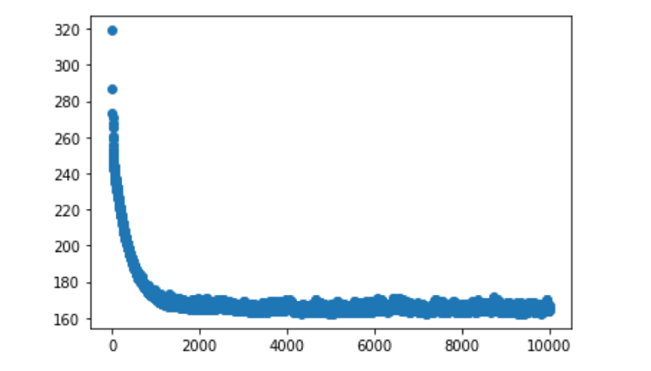
Мы видим стремительное падение примерно после 1000 итераций, и после этого изменений на графике практически не наблюдается. Это говорит нам о том, что для данной конкретной модели мы можем запустить алгоритм обучения не на 10 000, а всего на 1000 или 2000 итераций. Тем не менее, мы все равно получим схожие результаты.
В целом, функция ошибки предоставляет надежную информацию, помогающую определиться с тем, когда следует прекращать выполнение алгоритма. Очень часто такое решение основывается на доступном нам времени и вычислительной мощности. Однако есть и другие полезные факторы, на которые часто ориентируются специалисты в сфере данных. Выполнение алгоритма также прекращают в следующих случаях:
- когда функция потерь достигает определенного значения, которое мы заранее установили;
- когда функция потерь не уменьшается в течение нескольких эпох.
Что дальше?
Это был краткий обзор работы функции ошибки и того, как градиентный спуск помогает нам уменьшить ее. Но, думаю, вы уже поняли, что есть масса других моментов, которые я не стал затрагивать в этой статье, чтобы не перегружать вас. Если у вас возникли дополнительные вопросы, можете заняться самообразованием и продолжать “копать” в этом направлении дальше.
Тем не менее, представленный в этой статье материал должен дать вам базовое представление о том, как работает большинство моделей. Наверняка вы убедились в том, что вам не нужны глубинные познания в математике, чтобы понять принципы машинного обучения!
В следующей статье мы рассмотрим другую форму подгонки, а именно полиномиальную подгонку к данным (а не линейную) и будем использовать ее в дальнейшем, чтобы понять, как можно спасти наши модели от “недо/переподгонки”.
Самое главное, мы поймем, как функции ошибок и концепция градиентного спуска помогают регулировать веса, находить лучшее решение при оптимальном завершении процесса, и узнаем, как определить, что наша модель действительно работает!
Эта статья, как и многие другие, была написана под впечатлением от книги, которую я сейчас читаю — “Grokking Machine Learning” Луиса Серрано. Книга еще не вышла, но я приобрела ранний доступ к ней и думаю, что поступила правильно. Я считаю, что книги/материалы этого автора определенно заслуживают того, чтобы их прочитал каждый, кто хочет получить полное представление об алгоритмах и о том, как работают модели МО.
Читайте также:
- Создание модели машинного обучения с помощью Google Colab без дополнительных настроек
- 6 концептов книги Эндрю Ына «Жажда машинного обучения»
- Самая лучшая идея в науке о данных
Читайте нас в Telegram, VK и Дзен
Перевод статьи Anushree Chatterjee, #03TheNotSoToughML | Regression: Errors → Descending from a Mountain Top