Доходчиво об обучении на основе многообразий с алгоритмами IsoMap, t-SNE и LLE

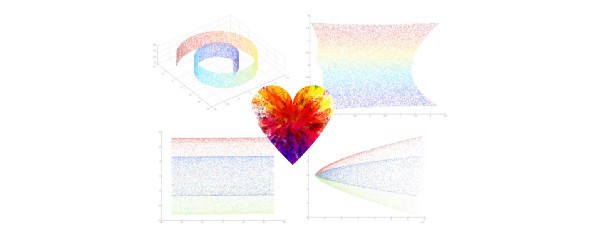
Метод главных компонент (PCA) весьма производителен, но зачастую дает сбой, так как предполагает возможность линейного моделирования данных. Он выражает новые признаки в виде линейных комбинаций существующих, умножая каждую на коэффициент. В целях преодоления ограниченности PCA был разработан ряд техник для применения к данным с различными характерными структурами. Однако обучение на основе многообразий ставит задачей найти метод, который сможет охватить все структуры данных.

В разных структурах данные имеют разные отношения между друг другом. Например, они могут быть линейно разделимы или очень разреженными. Отношения одних данных к другим бывают касательными, параллельными, охватывающими или ортогональными. PCA отлично работает с очень специфичными подвидами структур данных, поскольку предполагает их изначальную линейность.

Чтобы представить это в контексте, рассмотрите снимки головы размером 300 х 300 пикселей. В идеальных условиях каждое изображение будет в совершенстве отцентрировано, но в реальности нужно учесть много дополнительных условий, например освещение или наклон лица. Если мы рассмотрим снимок головы в виде точки в 90,000-мерном пространстве, то изменение таких эффектов, как наклон головы или направление взгляда, будет смещать ее в пространстве нелинейно, несмотря на то, что она будет оставаться все тем же объектом того же класса. 

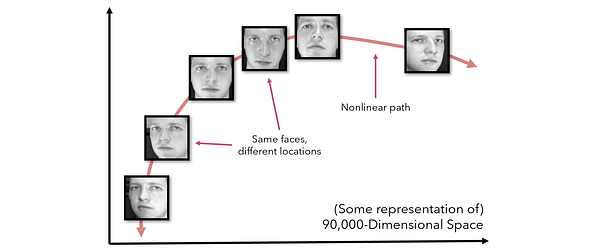
В реальных датасетах такой вид данных встречается очень часто. В дополнение к описанному эффекту, PCA путается при получении искаженных представлений, экстремальных значений и множества мнимых переменных в прямой унитарной кодировке. В данном случае возникает необходимость в обобщаемом методе уменьшения размерности. 

Обучение на основе многообразий как раз относится к этой задаче. Внутри данного вида обучения существует множество подходов, которые, вероятно, вы уже встречали. К их числу относятся t-SNE и локально-линейное вложение (LLE). Технические и математические детали данных алгоритмов описаны во многих статьях, но в данной мы сконцентрируемся на их общем понимании и реализации.

Обратите внимание, что хоть и существует несколько вариантов контролируемого уменьшения размерности (например, линейный/квадратичный анализ дискриминант), обучение многообразием относится к неконтролируемому уменьшению, при котором класс, хоть и может существовать, но алгоритму не представлен.

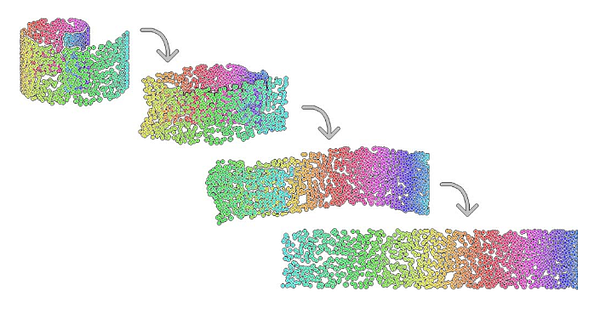
В то время как PCA стремится создать для представления размерностей несколько линейных гиперплоскостей, во многом аналогично построению регрессии для оценки данных, обучение на основе многообразий стремится обучать многообразия, представленные гладкими, изогнутыми поверхностями внутри многомерного пространства. Как показано на рисунке ниже, они зачастую формируются посредством тонких трансформаций изображения, которое в противном случае обмануло бы PCA.

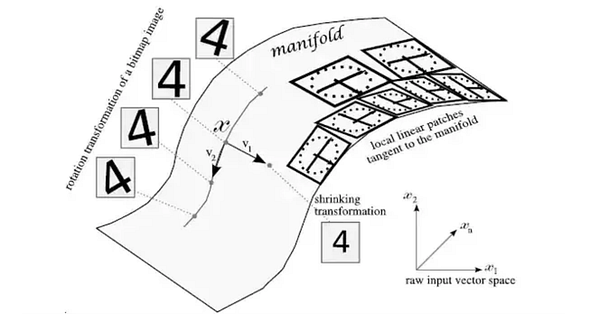
После чего можно извлечь “локальные линейные вставки” которые касательны к многообразию. Как правило, для точного представления данного многообразия этих вставок вполне достаточно. Поскольку подобные многообразия моделируются не какой-либо одной математической функцией, а несколькими небольшими линейными участками (патчами), такие линейные соседи способны моделировать любое многообразие. Несмотря на то, что сам процесс моделирования многообразий конкретными алгоритмами может не быть очевидным, в основе него лежат те же принципы. 

Далее перечислены фундаментальные аспекты алгоритмов обучения на основе многообразий:

• В данных существуют нелинейные отношения, которые можно моделировать при помощи многообразий  —  гладких и не особо изогнутых (не очень сложных) поверхностей, охватывающих несколько измерений. Многообразия непрерывны.
• Поддерживать многомерную форму данных не обязательно. Вместо их “уплощения” или “проецирования” (как в случае с PCA) согласно определенным направлениям для сохранения общей формы, можно выполнить более сложные манипуляции, наподобие развертывания скрученной полосы или выворачивания сферы наружу. 
• Наилучший метод моделирования многообразий  —  это представление изогнутого пространства как составленного из нескольких соседних частей. Если каждая точка данных сможет сохранить расстояние не до всех остальных точек, а только до ближайших к ней, то геометрические отношения в таких данных можно удержать. 

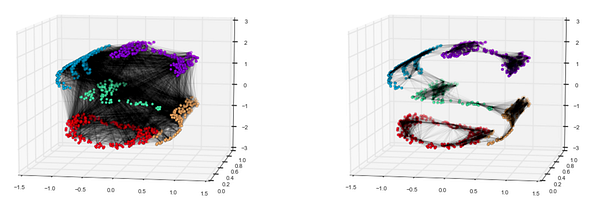
Эту идею легче понять, рассмотрев разные подходы по разворачиванию набора скрученных данных. Слева показан более похожий на PCA подход, направленный на сохранение формы данных, в котором все точки соединены между собой. Справа же представлен подход, в котором важно только расстояние между соседними точками данных.

Такое относительное пренебрежение к точкам, выходящим за рамки соседства, дает интересный результат. Рассмотрите в качестве примера набор данных Swiss Roll, который был скручен в трех измерениях и уменьшен до двухмерной полоски. В некоторых сценариях такой эффект оказался бы нежелательным. Тем не менее если эта кривая стала результатом, предположим, наклона снимающей изображение камеры или внешних эффектов, повлиявших на качество аудиозаписи, то обучение на основе многообразий разворачивает эти сложные нелинейные отношения очень кстати. 

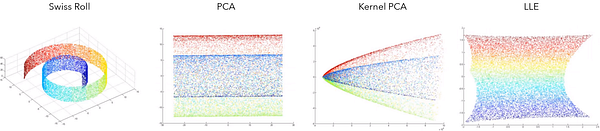
В наборе данных Swiss Roll подход PCA или даже более специализированные его вариации вроде Kernel PCA не справляются с захватом градиента значений. И напротив, алгоритм локально-линейных вложений (LLE) данную задачу выполняет.

Теперь давайте подробнее рассмотрим три основных алгоритма обучения на основе многообразий: IsoMap, локально-линейные вложения (LLE) и t-SNE.

Одним из первых исследований в области обучения на основе многообразий был алгоритм IsoMap, чье название расшифровывается как изометрическое отображение. Данный алгоритм стремится создать низкоразмерное представление, сохраняющее геодезические расстояния между точками. Геодезическое расстояние  —  это обобщение расстояния для изогнутых поверхностей. Таким образом, вместо измерения расстояния в чистой Эвклидовой форме с помощью формулы из теоремы Пифагора, IsoMap оптимизирует расстояния вдоль обнаруживаемого многообразия. 

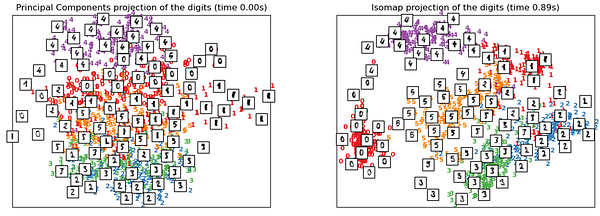
При обучении на датасете MNIST этот алгоритм выполняется лучше, чем PCA, правильно выделяя различные типы цифр. Близость и расстояние между конкретными группами цифр раскрывают структуру данных. Например, “5” и “3”, которые близки друг другу (см. снизу слева), на расстоянии действительно выглядят похоже. 

Ниже приведена реализация IsoMap на Python. Поскольку датасет MNIST очень велик, вы, возможно, обучите IsoMap только на первых 100 примерах, введя инструкцию .fit_transform(X[:100]).

from sklearn.datasets import load_digits #mnist
from sklearn.manifold import Isomap
X, _ = load_digits(return_X_y=True) #загрузка данных

embedding = Isomap(n_components=2) #итоговые данные имеют два измерения, 'components'
X_transformed = embedding.fit_transform(X) #fit model and transform

Локально-линейные вложения для моделирования многообразия задействуют ряд касательных линейных участков, как показано на диаграмме выше. Это можно представить как выполнение PCA для каждого из этих участков-соседей локально, создавая линейную гиперплоскость, а затем сравнивая результаты глобально для нахождения наилучшего нелинейного вложения. Цель LLE  —  развернуть или распаковать структуру данных искаженным образом, поэтому зачастую данный алгоритм будет иметь высокую плотность в середине с расширяющимися лучами.

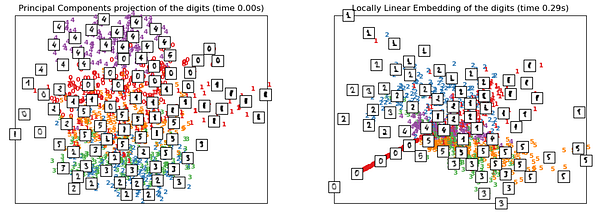
Обратите внимание, что производительность LLE в датасете MNIST относительно невысока. Причина тому, скорее всего, в том, что этот датасет состоит из нескольких многообразий, в то время как LLE спроектирован для работы с более простыми наборами данных вроде Swiss Roll. В данном случае справляется он примерно также как PCA или даже хуже. И это не удивительно, ведь его стратегия “представления одной функции в виде нескольких уменьшенных линейных” не может успешно работать с большими и сложными структурами датасетов. 

Ниже приведена реализация LLE, предполагающая, что набор данных (x) уже загружен:

from sklearn.manifold import LocallyLinearEmbedding
embedding = LocallyLinearEmbedding(n_components=2) #результат имеет два измерения
X_transformed = embedding.fit_transform(X)

t-SNE  —  это один из наиболее популярных выборов для высокоразмерной визуализации и обозначает t-распределенное стохастическое вложение соседей. Данный алгоритм преобразует связи в исходном пространстве в t-распределения или нормальные распределения с небольшими размерами выборок и относительно неизвестными стандартными отклонениями. Это делает t-SNE очень чувствительным к локальной структуре, что достаточно распространено при обучении на основе многообразий. Данный метод является наиболее популярным подходом к визуализации, поскольку обладает рядом преимуществ:

• Он способен раскрывать структуру данных в нескольких масштабах.
• Он раскрывает данные, лежащие во множестве многообразий и кластеров.
• Он имеет меньшую склонность к кластеризации точек в центре. 

IsoMap и LLE лучше всего подходят для разворачивания одного непрерывного низкоразмерного многообразия. И наоборот, t-SNE фокусируется на локальной структуре данных, стараясь извлечь кластеризованные локальные группы вместо того, чтобы пытаться развернуть их. Это дает данному алгоритму преимущество при распутывании высокоразмерных данных с множеством многообразий. Он обучается при помощи градиентного спуска и стремится минимизировать энтропию между распределениями. В этом смысле он очень похож на упрощенную неконтролируемую нейронную сеть.

t-SNE отличается высокой производительностью, потому что в обучении на основе многообразий использует подход ‘кластеризации’, а не “развертывания”. При работе с таким высокоразмерным датасетом, имеющим множество многообразий, как MNIST, в котором вращения и сдвиги вызывают нелинейные связи, t-SNE показывает себя даже лучше, чем LDA, которому были даны метки. 

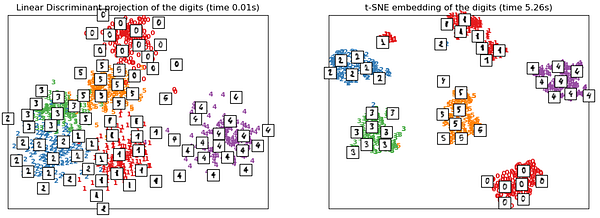
Тем не менее у t-SNE также есть и недостатки:

• Он требует больших вычислительных затрат  —  сравните время выполнения на диаграммах выше. Ему может потребоваться несколько часов для обработки датасета с миллионом выборок, в то время как PCA может управиться за несколько секунд или минут. 
• Этот алгоритм при выборе начальных значений для построения вложений полагается на случайность (стохастичность), что может увеличить время выполнения и понизить производительность в случаях, когда начальные значения выбраны неудачно. 
• Глобальная структура хранится не явно, т.е. ударение делается на кластеризации, а не ее демонстрации. Тем не менее в реализации sklearn эту проблему можно решить, инициализировав точки с помощью PCA, который построен специально для сохранения глобальной структуры.

t-SNE также можно реализовать в sklearn:

from sklearn.manifold import TSNE
embedding = TSNE(n_components=2) #результат имеет два признака
X_transformed = embedding.fit_transform(X)

В случае генерации t-SNE плохого результата его создатель, Лоренс ван дер Маатен, предлагает следующее:

В качестве проверки работоспособности попробуйте выполнить обработку ваших данных алгоритмом PCA, чтобы уменьшить их до двух измерений. Если в итоге вы снова получите плохой результат, вероятно, структура этих данных недостаточно хороша. Если же PCA справится успешно, а t-SNE  —  нет, то вы точно сделали что-то не так.

Почему он так говорит? В данном случае, чтобы расставить все по своим местам, уточним, что обучение на основе многообразий  —  это не очередная вариация PCA, а обобщение. Все, что хорошо выполняется в PCA, практически гарантированно будет также хорошо выполняться и в t-SNE или другой технике обучения на основе многообразий, поскольку все они являются обобщениями. 

Это можно сравнить с объектом, являющимся яблоком, а также в обобщенном смысле фруктом. Поэтому если выдаваемый алгоритмом результат не совпадает с его обобщенной версией, то значит что-то здесь не так. С другой стороны, если оба метода не справляются, то, вероятно, данные слишком сложны для моделирования.

Ключевые моменты

• PCA не справляется с моделированием нелинейных связей, потому что сам является линейным. 
• Нелинейные связи появляются в датасетах зачастую из-за того, что внешние силы вроде освещения или наклона могут нелинейно смещать в Евклидовом пространстве точки данных одного класса.
• Обучение на основе многообразий стремится обобщать PCA для выполнения уменьшения размерности во всех видах структур датасетов. При этом основная идея в том, что многообразия или изогнутые непрерывные поверхности должны моделироваться путем сохранения и доминирования локальных расстояний перед глобальными.
• IsoMap стремится сохранить геодезическое расстояние или расстояние, измеряемое не в Эвклидовом пространстве, а на изогнутой поверхности многообразия. 
• Локально-линейные вложения можно рассматривать как многообразие, представленное в виде нескольких линейных участков, для которых выполняется PCA.
• t-SNE вместо “развертывания” использует подход “извлечения”, но, как и другие алгоритмы обучения на основе многообразий, отдает приоритет сохранению локальных расстояний, используя вероятность и t-распространения.

Читайте также:

• Не слушай профи - делай print()
• 25 наборов аудиоданных для исследований
• Крутые наборы данных для машинного обучения

Читайте нас в Telegram, VK и Яндекс.Дзен

---

Перевод статьи Andre Ye: Manifold Learning [t-SNE, LLE, Isomap, +] Made Easy