Наука о данных

Безградиентный подход к оптимизации нейронной сети

27.09.2020

Градиентный спуск — это одна из важнейших идей в области машинного обучения, в котором алгоритм с учетом функции затрат итеративно выполняет шаги с наибольшим уклоном вниз, и, спустя достаточное число циклов, теоретически завершается в точке минимума. Впервые открытый Коши в 1847 и позднее расширенный Хаскеллом Карри в 1944 для задач нелинейной оптимизации градиентный спуск использовался для всех видов алгоритмов, начиная с линейной регрессии и заканчивая глубокими нейросетями.

Несмотря на то, что этот метод и его видоизмененная версия в виде обратного распространения ошибки (backpropagation) явили величайший прорыв в машинном обучении, оптимизация нейронных сетей остается неразрешенной проблемой. В интернете многие доходят до заявлений, что “градиентный спуск отстой”. Несмотря на то, что такие утверждения, конечно, перебор, у этой методики действительно есть ряд проблем:

Оптимизаторы застревают в достаточно глубоком локальном минимуме. Нужно признать, что есть грамотные решения, позволяющие иногда обходить такие проблемы. Например, импульс, способный переносить оптимизаторы через большие подъемы, или пакетная нормализация, сглаживающая пространство ошибок. Хотя причиной многих проблем ветвления в нейронных сетях по-прежнему остается локальный минимум.

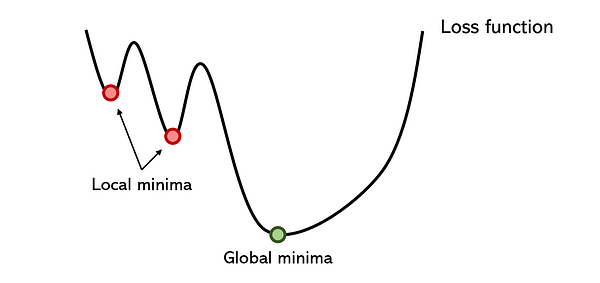
Поскольку оптимизаторы захватываются локальными минимумами достаточно сильно, то, даже умудряясь выйти из него, они затрачивают на это очень много времени. Градиентный спуск из-за своего низкого показателя конвергенции обычно представляет собой длительный метод даже с такими вариантами адаптации для больших наборов данных, как пакетный градиентный спуск.
Он особо чувствителен к инициализации оптимизатора. Например, производительность может быть существенно выше, если оптимизатор инициализируется возле второго локального минимума, а не первого, но все это определяется произвольно.
Темпы обучения обуславливают степень уверенности и рискованности оптимизатора. Установка завышенного темпа обучения может привести к пропуску глобального минимума, в то время как заниженная скорость чересчур увеличивает время выполнения. Для решения данной проблемы темпы обучения уменьшаются постепенно, но выбрать скорость уменьшения с учетом многих других переменных, определяющих ее, достаточно сложно.
Для градиентного спуска требуются градиенты. Это означает, что он уязвим для свойственных им проблем вроде затухающих или взрывающихся градиентов и все это в дополнение к его неспособности обрабатывать недифференцируемые функции.

Конечно же, градиентный спуск всесторонне изучался, и было предложено множество решений. Одни из них являются его вариациями, а другие основываются на архитектуре сети и работают лишь в некоторых случаях. То, что градиентный спуск явно переоценен еще не означает, что он не является наилучшим доступным на данный момент решением. Данная статья не ставит своей целью рассмотреть общеизвестные способы вроде применения пакетной нормализации для сглаживания пространства ошибок или выбор сложных оптимизаторов вроде Adam или Adagrad, хоть они и показывают более высокую производительность.

Вместо этого данное руководство нацелено на освещение более скрытых, но при этом очень интересных методов оптимизации, не входящих в стандартный перечень градиентных. Они, как и любая другая техника повышения производительности нейронной сети, исключительно хорошо работают в одних сценариях и не очень в других. Независимо от того, насколько хорошо они справляются с конкретной задачей, их можно отнести к удивительной, креативной и многообещающей области исследования для будущего машинного обучения.

Оптимизация методом роя частиц (PSO) — это основанный на популяции метод, который определяет набор ‘частиц’, исследующих область поиска для обнаружения минимума. PSO итеративно улучшил предполагаемое решение в отношении определенного показателя качества. Он решает задачу, используя популяцию потенциальных решений (“частиц”) и перемещая их согласно простым математическим правилам, таким как положение частицы и ее скорость. Каждое перемещение частицы определяется наилучшей, с ее точки зрения, локальной позицией, но также и лучшими позициями в пространстве поиска, найденными другими частицами. В теории рой через серию итераций перемещается по направлению к наилучшим решениям.

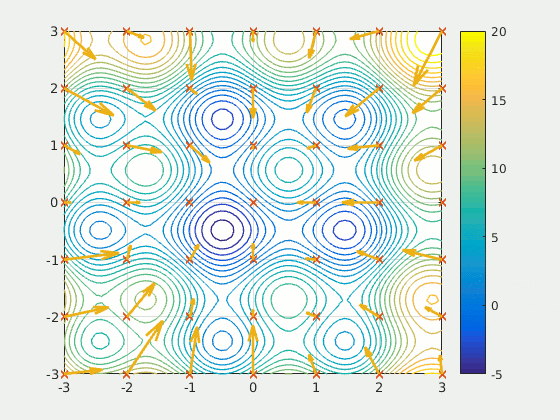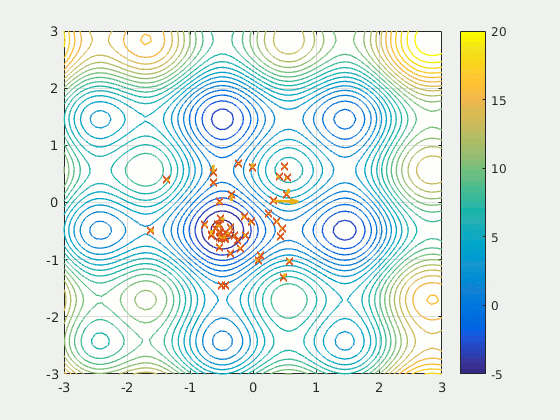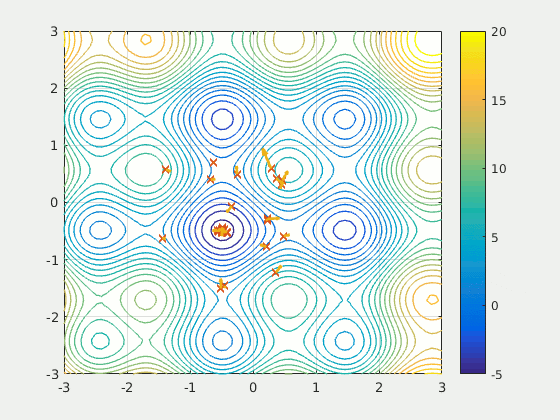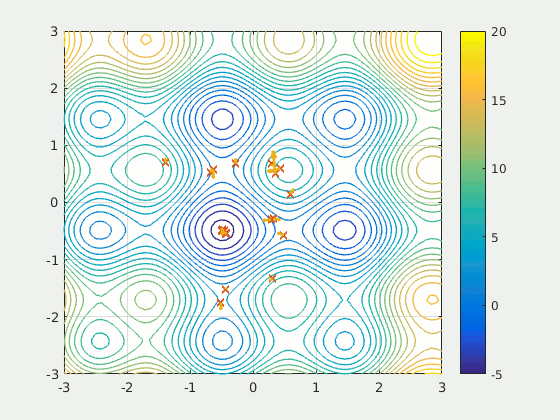
PSO можно назвать удивительным решением — оно намного менее чувствительно к инициализации, чем нейронная сеть, а обмен результатами между частицами может оказаться очень полезным методом поиска для разреженных и больших областей.

Поскольку PSO не основывается на градиентах, для него не требуется дифференцируемость проблемы оптимизации. В связи с этим его применение для оптимизации нейронной сети или любого другого алгоритма обеспечит большую свободу и меньшую чувствительность при выборе активации функции или в другой аналогичной роли. Кроме этого, он практически не делает предположений в отношении оптимизируемой задачи и может выполнять поиск на очень больших пространствах.

Здесь можно предположить, что основанные на популяции методы могут оказаться существенно дороже в плане вычислений по сравнению с градиентными оптимизаторами, но это не обязательно так. Благодаря его открытости и эластичности, характерным для основанных на эволюции алгоритмов, у нас есть возможность контролировать число частиц, их скорость, количество распределяемой глобально информации и т.д. Это аналогично настройке темпов обучения в нейронной сети.

Суррогатная оптимизация — этометод оптимизации, моделирующий функцию потерь с помощью другой хорошо налаженной функции с целью нахождения минимума. Эта техника выбирает из функции потерь “точки данных”, т.е. пробует разные значения для параметров (x) и сохраняет значение функции потерь (y). После сбора достаточного числа точек данных суррогатная функция (в данном случае полином 7-й степени) согласуется с ними.

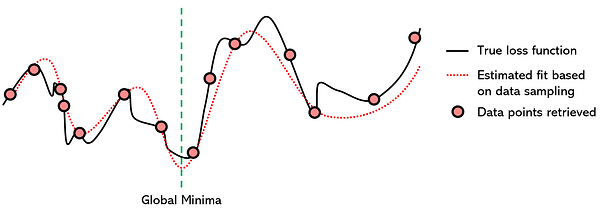
Поскольку нахождение минимума полиномов уже достаточно хорошо изучено и существует множество эффективных методов обнаружения их глобального минимума при помощи производных, можно предположить, что для функции потерь и суррогатной функции он будет одинаков.

Технически суррогатная оптимизация не является итеративным методом, хотя ее обучение зачастую именно таково. Помимо этого, она также не относится к градиентным методам, хотя зачастую эффективные математические методы нахождения глобального минимума моделирующей функции основываются на производных. Однако, поскольку как итеративные, так и градиентные свойства в случае с суррогатной оптимизацией являются вторичными, она может обрабатывать большой объем данных и недифференцируемые задачи оптимизации.

Оптимизация, использующая суррогатную функцию, весьма продумана в нескольких смыслах:

По-сути, она сглаживает поверхность истинной функции потерь, что уменьшает “зубчатые” локальные минимумы, из-за которых так сильно увеличивается время обучения нейронных сетей.
Она преобразует сложную проблему в гораздо более простую: будь то полином, RBF, GP, MARS или иная суррогатная модель, задача по нахождению глобального минимума усиливается математическими знаниями.
Чрезмерное обучение суррогатной модели не представляет собой большую проблему, поскольку даже в таких случаях суррогатная функция по-прежнему остается более гладкой и менее “зубчатой”, чем истинная функция потерь. Таким образом, наряду со многими другими привычными способами построения упрощенных и ориентированных на математику моделей, обучение суррогатных моделей намного проще.
Суррогатная оптимизация не ограничивается представлением того, где она находится в данный момент, поскольку видит “всю функцию”, в отличие от градиентного спуска, который должен непрерывно делать рискованные выборы, решая, будет ли за следующим подъемом более глубокий минимум.

Суррогатная оптимизация практически всегда будет быстрее градиентного спуска, но зачастую в ущерб точности. Она позволяет определить только приблизительное положение глобального минимума, но это все равно может оказаться чрезвычайно полезным.

Альтернативой является гибридная модель, где суррогатная оптимизация используется для приведения параметров нейронной сети к приблизительному местоположению, откуда далее для нахождения глобального минимума можно применять градиентный спуск. Другая альтернатива — использовать суррогатную модель для управления решениями оптимизатора, поскольку суррогатная функция:

может видеть наперед;
менее чувствительна к конкретным подъемам и спускам функции потерь.

Метод имитации отжига — это метод, работающий по принципу отжига в металлургии, при котором материал нагревается выше температуры собственной кристаллизации для изменения его физических и иногда химических свойств. После этого его постепенно остужают, возвращая в твердое состояние.

Используя понятие постепенного охлаждения, имитация отжига медленно уменьшает вероятность принятия худших решений по ходу исследования их пространства. Так как допущение худших решений формирует более обширное пространство поиска глобального минимума, имитация отжига предполагает, что возможности соответствующим образом представлены и изучены в первых итерациях. С течением времени алгоритм постепенно переходит от изучения к применению.

Ниже приведено примерное описание работы алгоритма имитации отжига:

Температура устанавливается в некое изначальное положительное значение и прогрессивно смещается к нулю.
В каждый шаг времени алгоритм произвольно выбирает решение, близкое к текущему, измеряет его качество и перемещается к нему в зависимости от текущей температуры, определяющей вероятность принятия лучших или худших решений.
В идеале к моменту достижения нулевой температуры алгоритм сводится к решению глобального минимума.

Имитацию можно выполнить с помощью кинетических уравнений или методов вероятностной выборки. Этот метод применялся для решения задачи странствующего моряка, стремящегося найти кратчайший путь между сотнями локаций, представленных точками данных. Очевидно, что число комбинаций бесконечно, но имитация отжига с элементами обучения с подкреплением справляется очень успешно.

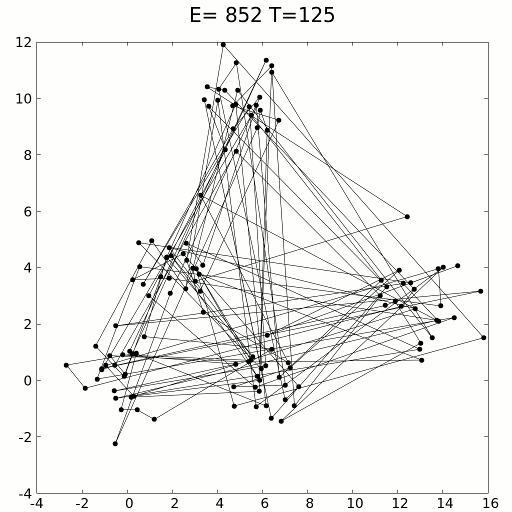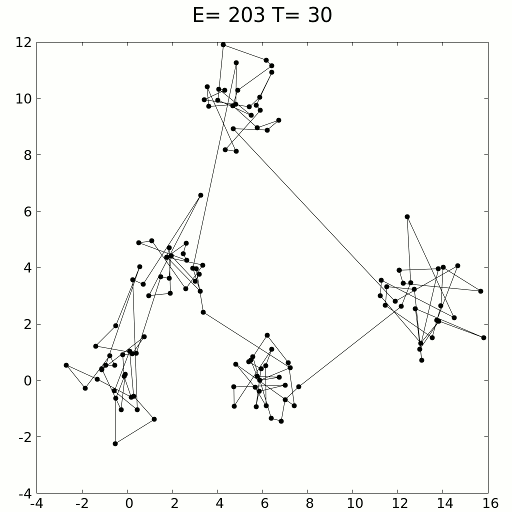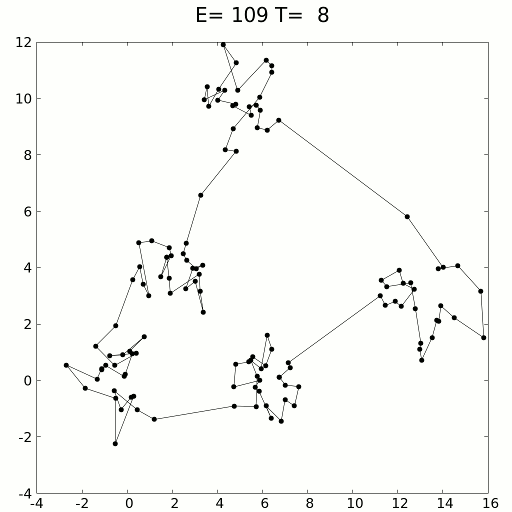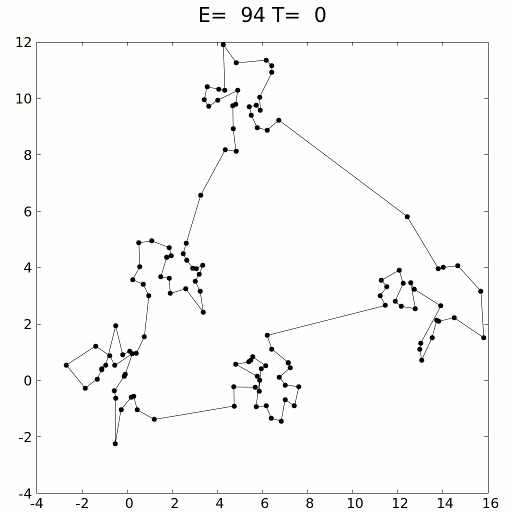
Решение задачи странствующего моряка при помощи имитации отжига

Имитация отжига особенно хорошо проявляет себя в сценариях, где приблизительное решение нужно получить за короткий период времени, опережая при этом медлительный градиентный спуск. Как и суррогатную оптимизацию ее можно использовать в тандеме с градиентным спуском, чтобы задействовать преимущества обоих способов: скорость имитации отжига и точность градиентного спуска.

Вывод

Мы рассмотрели небольшую выборку безградиентных методов. Существует множество других достойных изучения алгоритмов вроде поиска шаблона и мультикритериальной оптимизации. Генетические и основанные на популяции методы вроде оптимизации роя частиц выглядит весьма многообещающе для создания по истине “умных” агентов, учитывая, что мы, люди, являемся доказательством их успеха.

Применение безградиентных методов для оптимизации поражает креативностью, не ограниченной математическими цепочками градиентов. Никто не ожидает, что они станут мейнстримом, потому что градиентная оптимизация, несмотря на множество проблем, справляется со своей задачей очень хорошо. Тем не менее совмещение безградиентных и градиентных методов с гибридными оптимизаторами демонстрирует невероятно высокие возможности, особенно в эпоху достижения предела вычислительных мощностей.