Сервис балансировки нагрузки на ПИД-регуляторах — умозрительный пример

Недавно я наткнулся на технический блог Dropbox, в котором рассказывалось об их последней версии Robinhood (собственного сервиса балансировки нагрузки). Он предназначен для динамической регулировки весов узлов, чтобы равномерно распределять нагрузку при помощи пропорционально-интегрально-дифференциальных (ПИД) регуляторов.

У меня всегда были смутные воспоминания о теории управления, но никогда не было возможности применить ее на практике. Итак, я решил провести рождественский вечер, реализуя ПИД-регулятор (мини-версию сервиса Robinhood на Python) и наблюдая, насколько хорошо он работает в симуляции. Да, у меня плохие навыки поиска — в интернете я не смог найти ни одного хорошего ресурса, объясняющего реализацию ПИД-регулятора. Итак, этот пост предназначен для меня и моих коллег — незнакомцев, которые пытаются понять ПИД-регулятор.

Что такое ПИД-регулятор?

Пропорционально-интегрально-дифференциальный регулятор (ПИД- или трехчленный регулятор) — это механизм обратной связи на основе контура управления. Обычно он используется, чтобы управлять машинами и процессами, требующими непрерывного контроля и автоматической регулировки.

Версия проще:

ПИД-регулятор — прекрасная система. Он получает какие-то входные данные, вычисляет разницу между фактическими и желаемыми выходными значениями, а затем автоматически регулирует управляющий ввод, чтобы итоговый вывод был близок к желаемому значению. Проще говоря, входные данные — это переменные процесса, желаемое выходное значение — это заданное значение; разница между фактическим и желаемым значением — это частота ошибок. ПИД-регулятор настраивает переменные процесса так, чтобы поддерживать частоту ошибок как можно ближе к нулю.

Как следует из названия, он состоит из трех компонентов

1. Пропорционально — реагирует на текущую ошибку. Больше ошибка — больше корректировка.
2. Интегрально — учитывает прошлые ошибки, чтобы избавляться от накопленных статических ошибок.
3. Дифференциальный — прогнозируют будущие ошибки, реагируя на скорость изменения ошибок.

ПИД-регуляторы — супергерои промышленных инженеров, но у них также есть несколько интересных вариантов применения и в области информатики. Разберемся подробнее: разобьем его на математические уравнения и сохраним пример под рукой, чтобы увидеть, как он работает на самом деле.

Пример. У нас есть автомобиль, он движется со скоростью 50 км/ч. Нужно скорректировать эту скорость и поддерживать ее равной 60 км/ч.

1. Расчет ошибки

Чтобы получить ошибку, просто вычтите два значения выше (текущее значение из заданного). Пусть e(t) — ошибка в момент времени t. В нашем примере она будет 60–50 = 10 км/ч.

2. Пропорция

Чтобы отреагировать на текущую ошибку, нужна константа масштабирования (назовем ее Kp). Она связывает размер ошибки с размером входных данных.

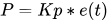
Итак, если Kp = 2, то P = 2 * 10 = 20, это и есть значение открытия дроссельной заслонки, которое нам нужно, чтобы приблизить скорость к 60 км/ч. Но если текущая скорость автомобиля 59 км/ч, то ошибка составит 1 км/ч. Пропорциональный ответ может оказаться слишком мал, чтобы преодолеть этот разрыв. Как разрешить проблему? Поприветствуем еще одного нашего друга — это интеграл.

3. Интеграл

Как и говорилось выше, он решает проблему статических ошибок. Ошибка с 1 км/ч — это статическая ошибка.

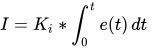
Итак, если сохранить значение Ki равным 0,5, то через 10 секунд имеем такое увеличение заслонки:

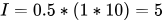
Идеально, мы перешли на скорость 60 км/ч.

4. Дифференциал

Производная прогнозирует будущие ошибки по скорости изменения ошибки. Это поможет предотвратить избыточное регулирование, ведь иногда P и I могут запутаться.

Допустим, автомобиль движется со скоростью от 55 км/ч до 60 км/ч, поэтому по мере приближения к заданному значению (60 км/ч) ошибка очень быстро уменьшается. При скорости 55 км/ч ошибка равна 5, при 58 км/ч — 2, а при 59,5 км/ч — 0,5. Таким образом, система может превысить скорость 60 км/ч, ведь P и I по мере приближения автомобиля к заданному значению не замедляют свои корректировки.

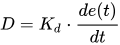
При Kd = 1, когда ошибка изменяется с 2 до 0,5 за 1 секунду, D станет равным -1,5. Это означает закрытие дроссельной заслонки.

5. Выходной сигнал ПИД-регулятора

Это не что иное, как сумма значений производной, интеграла и дифференциала:

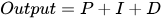
Я знаю, что сейчас это скучно. А как насчет того, чтобы взять практический пример и попытаться закодировать его, чтобы увидеть, имеет ли это смысл вообще?

Разработка Mini-Robinhood

Соберем мини-версию Robinhood. У нас есть куча узлов. К каждому узлу прикреплен вес. Вес определяет, какой объем трафика получит узел — это очень известный алгоритм взвешенного циклического перебора LB. Цель состоит в том, чтобы удостовериться, что нагрузка на каждый узел близка к средней нагрузке. Мы сделаем это при помощи ПИД-регулятора, который будет регулировать вес узлов динамически.

Поехали.

Шаг 1 — класс ПИД-регулятора

class PIDController:
    def __init__(self, kp, ki, kd):
        self.kp = kp # усиление пропорции
        self.ki = ki # усиление интеграла
        self.kd = kd # усиление дифференциала
        self.prev_error = 0 # предыдущая ошибка для производной
        self.integral_error = 0 # суммарная ошибка для интеграла

    def compute(self, setpoint, current_value):
        """
        Вычисляет выходной сигнал ПИД-регулятора
        аргументы
            setpoint: целевое значение (средняя нагрузка)
            current_value: текущая нагрузка на данный узел

        возвращает
            корректировку, применяемую к весу узла
        """

        error = setpoint - current_value
        self.integral_error += error
        derivative = error - self.prev_error

        pid_output = self.kp * error + self.ki * self.integral_error + self.kd * derivative
        self.prev_error = error

        return pid_output

Шаг 2 — код Mini Robinhood и демонстрационный класс

import random 
from pid_controller import PIDController

# узлы с примерами весов и нагрузок
nodes = [
    { "node_id": 1, "weight": 0.5, "utilization": 1 },
    { "node_id": 2, "weight": 0.7, "utilization": 1 },
    { "node_id": 3, "weight": 0.4, "utilization": 1 },
]

# распределение траффика между узлами 
def distribute_traffic():
    total_weight = sum(node["weight"] for node in nodes)

    for node in nodes:
        node["utilization"] += random.uniform(0.05, 0.15) * ( node["weight"] / total_weight ) # просто распределяет трафик в соответствии с их весом

def avg_utilization():
    return sum(node["utilization"] for node in nodes) / len(nodes)

# --------- Демо Mini Robinhood ---- #
class MiniRobinhoodDemo:
    @staticmethod
    def run():
        # установка pid_controller для каждого узла
        pid_controllers = [
            PIDController(1, 0.1, 0.5) for _ in nodes
        ]

        # симуляция в 10 итераций 
        for itr in range(10):
            print('Iteration: ', itr)

            avg_util = avg_utilization()
            print(f"Average Utilization: {avg_util}")


            # корректировка весов с помощью ПИД-регуляторов
            for index, node in enumerate(nodes):
                adjustment = pid_controllers[index].compute(avg_util, node["utilization"])
                node["weight"] += adjustment

                print(f"  Node {node['node_id']} - Utilization: {node['utilization']:.2f}, New Weight: {node['weight']:.2f}")

            distribute_traffic()

            print('----------------------------------')


        print('Done')

if __name__ == "__main__":
    MiniRobinhoodDemo.run()

Просто запустите run.

Вывод будет выглядеть так:

pankaj.tanwar@the2ndfloorguy-X0 mini-robinhood % python3 mini_robinhood.py
Iteration:  0
Average Utilization: 1.0
  Node 1 - Utilization: 1.00, New Weight: 0.50
  Node 2 - Utilization: 1.00, New Weight: 0.70
  Node 3 - Utilization: 1.00, New Weight: 0.40
----------------------------------
Iteration:  1
Average Utilization: 1.036338004761167
  Node 1 - Utilization: 1.03, New Weight: 0.51
  Node 2 - Utilization: 1.06, New Weight: 0.66
  Node 3 - Utilization: 1.02, New Weight: 0.43
----------------------------------
Iteration:  2
Average Utilization: 1.0746097021837298
  Node 1 - Utilization: 1.07, New Weight: 0.52
  Node 2 - Utilization: 1.10, New Weight: 0.63
  Node 3 - Utilization: 1.06, New Weight: 0.45
----------------------------------
Iteration:  3
..................

Он довольно ясно показывает, как веса корректировались динамически. Свободно меняйте решение на GitHub.

Варианты применения ПИД-регулятора

1. Автомобили с автоматическим управлением — автомобиль должен оставаться в центре полосы движения, компенсируя отклонения из-за поворотов дороги, ветра или, возможно, даже ошибок в системе сенсоров. ПИД-регулятор автоматически регулирует угол поворота, чтобы минимизировать разницу между положением автомобиля и центром полосы. Другие довольно распространенные случаи — это круиз-контроль, следование по траектории и моя любимая система управления подвеской.
2. Планировщики задач — регулятор может устанавливать приоритеты и распределять задачи, чтобы обеспечить эффективное использование ресурсов.
3. Cinnamon в Uber применил эту технологию столетней давности, чтобы собрать распределитель средней нагрузки.

Читайте также:

• 18 полезных скриптов автоматизации на Python. Часть 2
• Обучение LLM (и не только) на Go. С Python в люльке
• Метод SHAP для категориальных признаков

Читайте нас в Telegram, VK и Дзен

---

Перевод статьи Pankaj Tanwar: Building a tiny load balancing service using PID Controllers