Модели машинного обучения часто оцениваются по их производительности, близости какого-либо показателя к нулю или единице, но это не единственный фактор, которым определяется их полезность. В некоторых случаях модель, в целом не очень точную, можно откалибровать и найти ей применение. В чем же разница между хорошими калибровкой и производительностью, и когда одна предпочтительнее другой?
Калибровка вероятности
Калибровка вероятности — это степень, с которой прогнозируемые в модели классификации вероятности соответствуют истинной частотности целевых классов в наборе данных. Прогнозы откалиброванной модели в совокупности тесно соотносятся с фактическими результатами.
На практике это означает, что если из множества прогнозов идеально откалиброванной модели двоичной классификации учесть только те, для которых моделью предсказана 70%-ная вероятность положительного класса, то модель должна быть корректной в 70% случаев. Аналогично, если учесть только примеры, для которых моделью прогнозируется 10%-ная вероятность положительного класса, эталонные данные окажутся положительными в 1 из 10 случаев.
Прогнозы откалиброванной модели в совокупности тесно соотносятся с фактическими результатами.
Прогнозы откалиброванной модели гарантированно соответствуют не байесовскому, а частотному подходу в определении вероятности события как предела его относительной частоты во многих испытаниях.
Вероятность выпадания шестерки при бросании игральной кости — 1/6, то есть при многих бросаниях или испытаниях шестерка выпадает в среднем раз за каждые шесть бросаний. Чем больше бросаний, тем ближе к 1/6 частота выпадания шестерок. Что значит в этом контексте, когда в модели двоичной классификации выдается 90%-ная вероятность события? Если бросаний много, примерно в 9 из 10 случаев событие действительно произойдет.
Большинство ML-моделей откалибровано плохо, и причины этого кроются в алгоритме обучения. В древовидных ансамблях, например классификаторах на основе ансамбля случайного леса, прогнозы генерируются усреднением отдельных деревьев. Из-за этого нереально получение вероятностей, близких к нулю и единице, поскольку в прогнозах деревьев всегда имеется дисперсия. Вследствие этого вероятности далеки и от нуля, и от единицы. Многие другие модели оптимизируются и оцениваются по двоичным показателям. Точность обнаруживается лишь в отношении того, правы мы или нет, ее степень не учитывается. Критерий Джини, применяемый в деревьях решений для определения разделений, оптимизируется для максимальной точности и быстроты.
Поэтому, хотя в оценках большинства ML-моделей порядок сохраняется — выше число, вероятнее положительный класс, — они не интерпретируются как частотные вероятности.
Для их калибровки имеются простые методы, и хорошая калибровка для модели желательна. Но это не обязательное условие полезности модели, иногда ее калибровка даже не нужна.
Нужна ли вообще калибровка?
При обучении модели классификации важен вопрос: «Действительно ли модель нужно откалибровать?» Ответ зависит от того, как ее использовать. Рассмотрим примеры.
Калибровка — это все: определение лимита кредитной линии
В некоторых сценариях хорошая калибровка необходима. Например, в банке решают, какую сумму кредита предоставить клиенту. Рассматриваются только те заемщики, которые уже прошли отбор, имеют низкий уровень риска и обладают правом на получение кредита. Мы еще обсудим этот процесс отбора подробнее. Решение о предоставлении кредитов принято — вопрос в количестве денег для каждого заемщика.
Банку необходима точная вероятность дефолта для каждого клиента при разных суммах кредита. Зная вероятность различных сценариев, банкиры спрогнозируют финансовый эффект всех кредитов, погашенных и просроченных, и примут оптимальное решение. Для этого нужна хорошо откалиброванная модель.
Обратите внимание: точность модели здесь не важна. Важно быть с правильной стороны прогнозного порога. Нет разницы между прогнозом 51% и 99%: кредит будет просрочен в обоих случаях. Но для банка и самих заемщиков разница огромная. Здесь важно правильно рассчитать вероятность.
Калибровка — это все: оценка производительности модели
Иногда хорошая калибровка — необходимое условие применения модели. Как оценить производительность модели в продакшене, не зная целей эталонных данных? Эта сложная задача для моделей классификации решается с помощью алгоритма оценки производительности на основе достоверности. Идея этого подхода заключается в оценке элементов матрицы несоответствий на основе ожидаемых частот ошибок, которые нам известны, при условии что модель откалибрована.
Поэтому, чтобы отследить производительность модели в продакшене в отсутствие целей эталонных данных, модель нужно откалибровать. Опять же, большая точность ей не нужна, пока прогнозы модели откалиброваны.
Калибровка не нужна: задачи ранжирования
Однако бывают ситуации, в которых калибровка модели не важна. Сюда относятся всевозможные задачи ранжирования с моделями, в которых по качеству или релевантности поисковому запросу пользователя ранжируются заголовки новостных статей.
Если цель — выбрать одну или несколько статей для показа пользователю, важна не точная вероятность того, что каждая из них высококачественная и релевантная, важен порядок оценок модели. То есть нужно быть уверенным: то, что показывается пользователю, лучше того, что не показывается, а лучшие новости находятся в верхней части списка результатов. В этом случае в калибровке модели особого смысла нет.
Калибровка не нужна: предоставление кредитов
Другой пример сценария, в котором калибровка не важна, — отбор заемщиков для предоставления кредита.
Цель здесь — спрогнозировать, кто из них погасит свой кредит. В этой задаче двоичной классификации банк интересуют не вероятности модели, а точность ее классификации.
Хорошая калибровка либо необходима, либо не нужна — зависит от того, как модель использовать.
Обратимся теперь к моделям, которые не отличаются высокой производительностью, но благодаря хорошей калибровке очень полезны в сфере их применения.
История плохой, но откалиброванной модели
Рассмотрим две модели: от первой трудно добиться хорошей производительности, но модель ценна из-за хорошей калибровки. Во второй хорошая производительность теоретически невозможна, но модель полезна благодаря своей откалиброванности.
Когда трудно достичь хорошей производительности
Недавно я обучал модели прогнозировать результаты футбольных матчей: хотел легко и быстро зарабатывать на ставках у букмекеров. Дать точный прогноз — задача невыполнимая: здесь слишком много скрытых факторов, таких как удача и настрой игроков в день матча. Но точный прогноз и не нужен. Аналогично примерам с определением лимита кредитной линии и оценкой производительности, здесь все дело в правильном расчете вероятностей.
Рассмотрим этот двоичный классификатор на основе ансамбля случайного леса, обученный на паре сезонов матчей Английской премьер-лиги прогнозировать победу хозяев. В набор признаков включались рейтинги Эло обеих команд и статистика для оценки формы каждой команды в последних играх в атаке и защите.
Тестовая точность модели была 63%. Это лучше, чем у фиктивной модели (46%), в которой всегда прогнозируется победа хозяев: они, как правило, выигрывают почти половину игр. Однако 63% не кажется отличным результатом.
Рассмотрим калибровочные кривые модели. На горизонтальной оси показаны вероятности модели для тестового набора, разделенного на 10 одинаковых интервалов. Для каждой из них на вертикальной оси отражена фактическая частота побед хозяев. Идеально откалиброванная модель показана прямой диагональной линией:
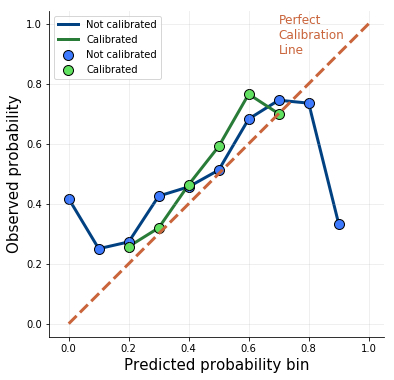
В исходной, синей модели очень плохая калибровка на экстремальных вероятностях: у прогноза в 90% лишь 30% шансов оказаться корректным. Я откалибровал модель одним из самых популярных методов: подгонкой параметра логистической регрессии на выходных данных модели.
В итоговой, зеленой модели калибровка гораздо лучше. У нее больше нет экстремальных вероятностей, а точность снизилась до 62%. То есть калибровку модели удалось улучшить за счет точности. Что это дает?
Подумайте о такой стратегии: делать ставки только на матчи с наибольшей вероятностью победы хозяев, то есть с прогнозом модели 70%. Благодаря достаточно хорошей калибровке модель корректна в 70% таких случаев.
Ставя на каждую игру по 100 $, из 100 игр мы проиграем 30 и потеряем 3000 $, но выиграем остальные 70 и получим 70 * 100 * (odds – 1). Вычитаем 1, ведь нужно еще потратить 7000 $ на купоны. Решая это уравнение, находим коэффициенты, при которых мы останемся при своих:
3000 = 7000 * odds - 7000
10000 = 7000 * odds
odds = 10000 / 7000 = 1,42
Итак, ставим на все матчи с прогнозом модели 70% и коэффициентом выше 1,42 (без учета налогов). Аналогично считаются коэффициенты для других прогнозных вероятностей. Если калибровка модели останется хорошей в будущем, эта стратегия со временем должна стать довольно прибыльной. И это несмотря на плохую точность — лишь 62%.
Когда невозможно достичь хорошей производительности
Теперь попробуем спрогнозировать выпадание чисел при бросании игральной кости. В модели должна выдаваться вероятность выпадания шестерки. Игральная кость — это обычный шестигранный кубик правильной формы для настольных игр.
Бросание такой кости — абсолютно стохастический процесс, и вероятность любой из ее сторон оказаться наверху одинакова: ⅙. Другими словами, классы данных совершенно неразделимы: точную модель построить невозможно. Тогда какой она будет?
Рассмотрим два альтернативных подхода. Модель A — это фиктивный двоичный классификатор, в котором всегда с полной достоверностью прогнозируется невыпадание шестерки, то есть шестерка прогнозируется в 0% случаев, остальные числа — в 100%. В модели B шестерка тоже никогда не прогнозируется, а вот вероятности здесь другие: шестерка всегда прогнозируется с вероятностью ⅙, остальные числа — с вероятностью ⅚.
У обеих моделей точность одинаковая: они корректны в 5 случаях из 6. Но имеется важное различие: модель B откалибрована идеально, а модель A не откалибрована вовсе. В этом модели разнятся максимально.
А как насчет их полезности? От модели А нет никакой реальной пользы. С помощью модели B в долгосрочной перспективе точно прогнозируется целевая частота и можно проводить моделирование для ответа на вопросы посложнее, например «Какова вероятность выпадания 7 шестерок при 11 бросаниях игральной кости?». Опять же, несмотря на низкую производительность, модель становится полезной благодаря хорошей калибровке.
Выводы
- Прогнозы откалиброванных моделей в совокупности тесно соотносятся с частотной фактических результатов. Большинство моделей откалибровано плохо из-за того, как они обучаются, но для их калибровки имеются простые методы.
- Для некоторых задач, таких как определение лимита кредитных линий и оценка производительности на основе достоверности, хорошая калибровка необходима и важнее самих метрик производительности. Для других, таких как предоставление кредитов и задачи ранжирования, гораздо важнее правильный порядок ранжирования и производительность.
- Неточные модели бывают весьма полезны, при условии что они откалиброваны — все дело здесь в правильном расчете вероятностей.
Читайте также:
- Как освоить машинное обучение
- Как преобразовать сгенерированные ИИ изображения в полигональные сетки
- Почему точные модели не всегда полезны
Читайте нас в Telegram, VK и Дзен
Перевод статьи Michał Oleszak: Bad machine learning models can still be well-calibrated






