Что такое подгонка линии?
Когда мы начинаем изучать любой курс по МО, первое, с чем мы сталкиваемся, — это проведение линии вблизи точек. В связи с этим вы часто можете встретить термин “линейная регрессия”.
Примечание. Хотя в этой статье пойдет речь в основном об интуитивных решениях, лежащих в основе линейной регрессии, мы также будем использовать уравнения.
Кстати, мы будем создавать эти уравнения самостоятельно!
Что нам нужно сделать?
Для начала определим, как мы будем подгонять линию. Посмотрите на точки, указанные на рисунке внизу. Похоже ли на то, что они “примерно” соответствуют форме линии?

Если бы мне нужно было провести линию через эти точки, вот лучший вариант, который пришел бы мне в голову:
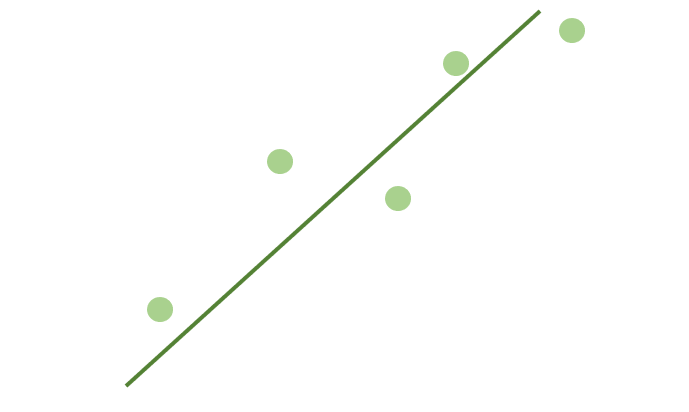
Допустим, вы представили себе точно такую же линию, как та, что изображена на рисунке. Это как раз и является назначением линейной регрессии.
Следовательно, наша цель (или, скорее, цель компьютера) состоит в том, чтобы нарисовать именно ЭТУ линию.
Зачем же нужен алгоритм?
Представим, что точки — это дома в городе. Нам нужно построить дорогу, которая была бы как можно ближе к каждому дому, чтобы жителям было легче добираться до нее.
Начиная думать о предстоящем проекте, мы сталкиваемся со множеством вопросов.
- Нужна ли дорога, которая находится близко ко “всем” домам, или мы построим ту, что будет располагаться близко к некоторым домам, но далеко от других?
- Что имеется ввиду под “точками, которые приблизительно принимают форму линии”?
- Что имеется ввиду под “линией (в данном случае дорогой), которая находится максимально близко к каждой точке (или дому)”?
Рассмотрим другой пример.
Допустим, мы хотим выяснить стоимость домов в городе, чтобы знать, сколько будет стоить дом нашей мечты. Мы знаем, что есть много факторов, которые могут повлиять на цену — местоположение, расстояние до рынка, размер дома, количество комнат и т. д. В мире МО эти факторы называются “признаками”.
Подобно тому, как признаки инструмента, будь то пианино или телескоп, описывают то, что представляет собой этот инструмент, так и признаки модели описывают то, из чего состоит “модель”. Модель — это правило или формула, которая прогнозирует “метки” на основе признаков. Метка — это то, зачем мы строим модель. Ее описывают признаки, и она является целью, которую нужно “спрогнозировать”. То, что мы прогнозируем, или сам прогноз — это выход модели.
Можем ли мы сформулировать уравнение на этом этапе? Можем ли построить модель, которая подскажет , “с какой силой и до какой степени” тот или иной признак влияет на метку — цену?
Взглянем на таблицу ниже.
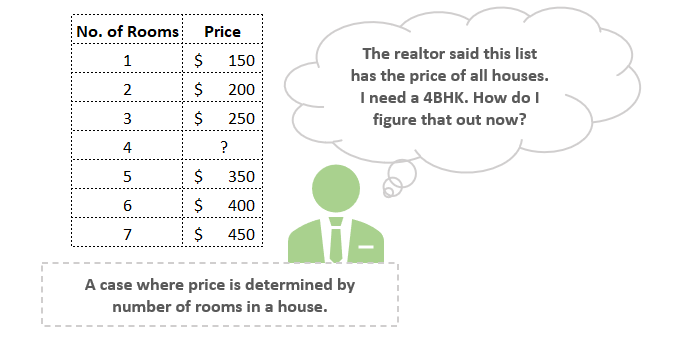
В приведенном выше примере мы допускаем, что только “количество комнат” влияет на цену дома. Как вы думаете, какое число следует вписать в то место, где стоит вопросительный знак?
Скорее всего, вы ответите, что “300 долларов”. И будете, конечно же, правы.
Вероятно, вы уже составили в уме следующее уравнение:
Цена = 100 + 50 х (количество комнат)
Таким образом, мы создали модель. Она прогнозирует цену дома на основании одного единственного признака (количества комнат). Цена дома является некоторым кратным числом (в данном случае — “50”) по отношению к количеству комнат в доме. Это число мы называем “весом”, а базовая цена дома, на которую не влияет признак, может быть принята за 100, и в МО это называется “смещение”.
Как мы пришли к этой формуле?
Вы, вероятно, обратили внимание на другие цены, выявили закономерность между количеством комнат и соответствующими ценами, построили формулу и, наконец, получили цену. Процесс, который произошел в вашей голове, это и есть линейная регрессия!
На данном этапе выделим 3 ключевых шага.
- Запоминание текущих точек.
- Формулировка уравнения.
- Прогнозирование недостающей точки.
Но что, если получить ответ было бы не так просто? Что если бы схема была намного сложнее (см. ниже)?
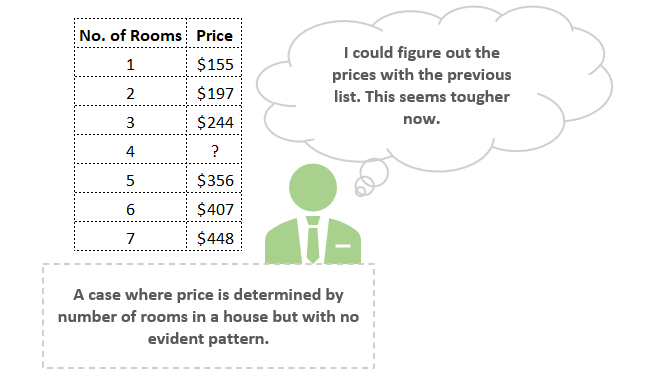
Кажется, что в этом случае уже гораздо труднее выявить закономерность, чем в предыдущем наборе данных. Попробуем использовать визуализацию.
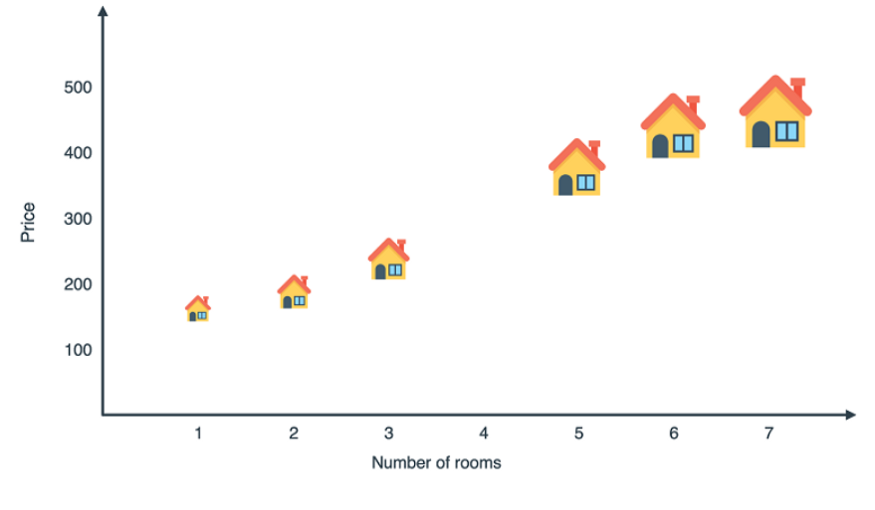
На самом деле, не так уж все и сложно. Но как же помочь компьютеру найти искомую линию?
Как компьютер находит линию
В МО большинство концепций работают, следуя простому принципу “шаг за шагом” или “бит за битом”.
Шаги, которым мы будем следовать, похожи на те, что мы обсуждали выше.
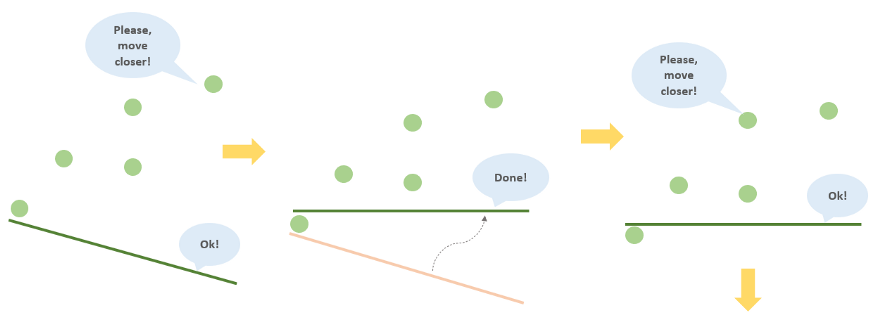
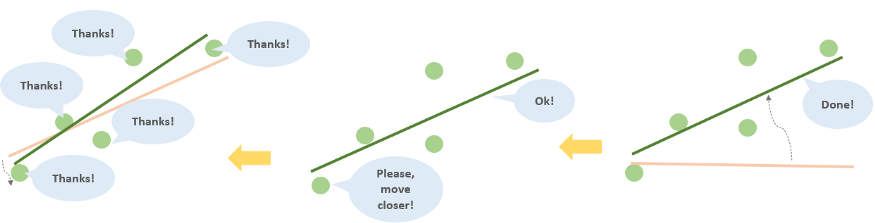
- Начнем с того, что заставим компьютер выбрать случайную линию.
- Запоминание: компьютер должен запомнить случайную точку данных.
- Формулировка: компьютер должен переместить линию немного ближе к этой точке.
- Многоразовый повтор шагов 2–3.
- Прогноз: компьютер должен вернуть полученную линию.
Теперь для более глубокого понимания процесса обратимся к математике (не волнуйтесь, ничего сложного не будет!).
p — цена дома в наборе данных.
r — количество комнат.
m — цена за комнату.
b — базовая цена дома.
Также будем работать с дополнительной переменной:
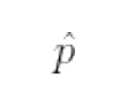
Это переменная, которая показывает прогнозируемую цену или, другими словами, прогноз модели.
Уравнение выглядит следующим образом:
p^= mr + b
Если мы опишем его словами, то получится следующее:
Прогнозируемая цена = (Цена за комнату) х (Количество комнат) + Базовая цена дома
Все выглядит вполне логично. Так это и есть та линия, которую должен был найти компьютер? Верно!
Теперь вы знаете, что означает “подогнать линию” или “подогнать алгоритм линейной регрессии”.
Чтобы еще раз продемонстрировать, как работает интуитивный подход, возьмем другой пример.
Допустим, у нас есть модель, в которой цена за комнату составляет $40, а базовая цена дома — $50. Модель предсказывает цену с помощью следующего уравнения:
p^ = 40 х r + 50
Предположим, в нашем наборе данных есть дом с 2 комнатами, который стоит $150. Наша модель предсказывает, что цена дома составит 40 х 2 + 50 = $130. Эта сумма близка к фактической, но все же меньше ее.
Возможно, проблема в том, что модель считает дом слишком дешевым. Есть ли способ улучшить прогноз? Действительно ли эта модель ориентируется на низкую базовую цену, или у нее более низкая оценка стоимости комнаты, или и то, и другое?
Попробуем немного поиграть с цифрами. Увеличим цену за комнату на $0,5, а базовую цену на $1.
Новое уравнение будет выглядеть следующим образом:
p^ = 40,5 х r + 51
Новая прогнозируемая цена для дома с 2 комнатами составит 40,5 х 2 + 51 = $132.
Этот результат уже ближе, чем предыдущий, к фактической цене $150. Наша модель, похоже, делает лучшие прогнозы с этими весами и смещением в отношении этой конкретной точки данных.
Наиболее важным моментом для линейной регрессии является многократное повторение вышеописанного процесса.
Подводя итог вышесказанному и говоря о том, к чему стремится линейная регрессия, можно составить следующий алгоритм.
- Выберите модель (линию) со случайными весами и случайным смещением.
- Выберите случайную точку данных.
- Слегка подкорректируйте веса и смещение, чтобы улучшить прогноз в отношении этой конкретной точки данных.
- Повторите шаги 2–3 много раз.
- Верните полученную итоговую модель/линию.
Обратите внимание, мы все еще следуем по пути “запоминай-формулируй-прогнозируй”. Мы просто разбили шаг “формулируй” на подэтапы.
Конечно, в этой статье речь шла об одной переменной. При попытке понять интуитивный подход, лежащий в основе таких алгоритмов, можно использовать одну единственную функцию, однако всегда нужно помнить о реальных жизненных ситуациях. В реальном мире на цену дома будет влиять множество признаков, как указано выше. Это называется многомерной линейной регрессией.
Когда у нас много признаков, мы умножаем каждый признак на соответствующий вес и добавляем их к прогнозируемой цене (как в примере ниже):
Цена = 30 х (количество комнат) + 1,5 х (размер) + 10 х (качество школ в округе) — 2 х (возраст дома) + 50
Вы заметили, что кроме “возраста дома”, все признаки имеют положительный вес. Это потому, что последние положительно коррелируют с ценой дома. Другими словами, чем больше дом (размер), тем выше будет цена. С другой стороны, поскольку мы ожидаем, что цена более старого дома будет ниже, признак возраста имеет отрицательную корреляцию и, следовательно, отрицательный вес.
В то время как “знак” веса указывает на “степень” корреляции признака с меткой (или нашей целевой переменной — ценой), “значение” веса указывает на “силу” или степень влияния признака на целевую переменную. Так, если признак имеет “нулевой” вес, это означает, что он никак не связан с целевой переменной (например, имена соседей, проживающих в городе). Аналогично, если признак имеет большой вес по сравнению с другими признаками (например, количество комнат имеет наибольший вес в приведенной выше модели), это означает, что данный признак действительно важен для определения цены дома.
Визуализация для таких моделей становится сложной задачей, поскольку модель представляет собой уже не просто “линию”, как в случае с одним признаком. Тем не менее ее можно представить как линейное уравнение.
Читайте также:
- Как учатся машины
- 25 прикольных вопросов для собеседования по машинному обучению
- Почему логарифмы так важны в машинном обучении
Читайте нас в Telegram, VK и Дзен
Перевод статьи Anushree Chatterjee: #01TheNotSoToughML| “Fit a line” — What do we even mean?






