Введение
Знакомство с машинным обучением часто начинается с линейной регрессии — одного из самых простых алгоритмов.
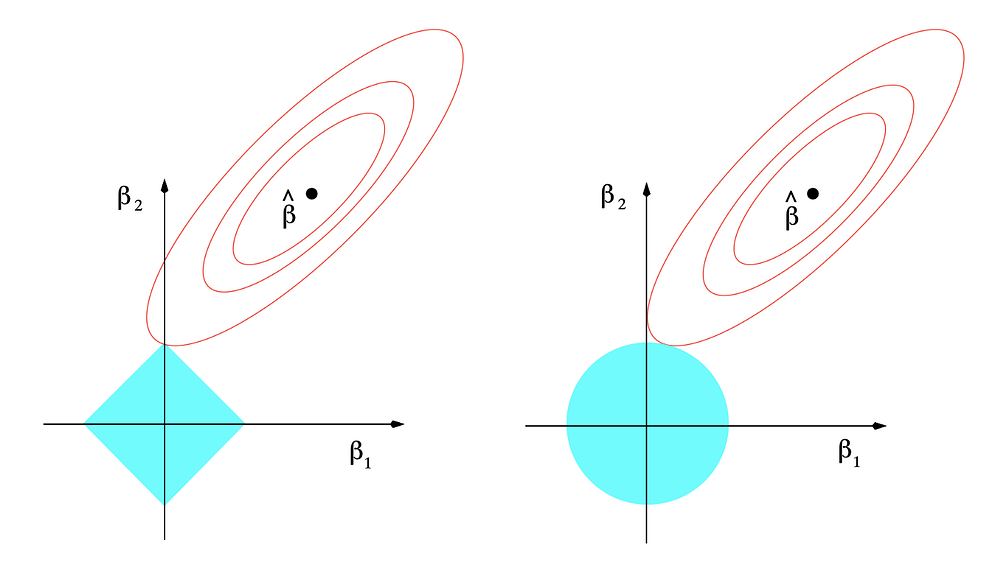
Однако эта модель быстро раскрывает свои недостатки, особенно при работе с наборами данных, которые требуют перестройки моделей. Основные решения этой проблемы — ридж- и лассо-регрессии.
Дилемма смещения-дисперсии
Чтобы понять, зачем нужны эти методы, обсудим дилемму смещения-дисперсии.
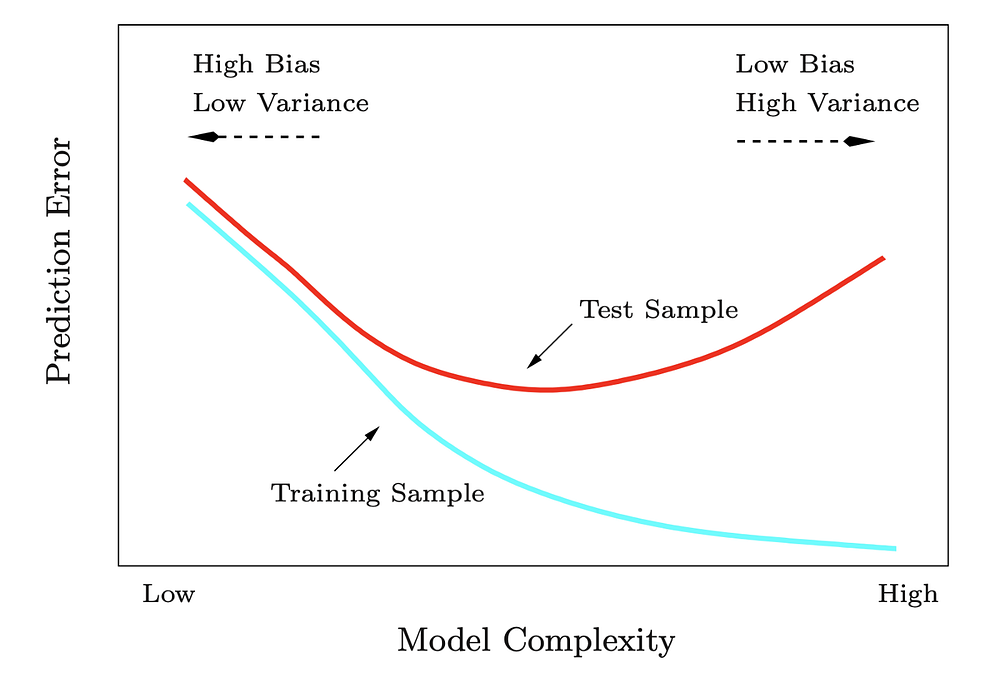
В контролируемой среде у модели может быть два основных источника ошибок.
- Смещение — ошибка, связанная с неверными предположениями в алгоритме обучения. Высокое смещение приводит к тому, что алгоритм упускает значимые взаимосвязи между признаками и целью (также называется “недостаточно близкой подгонкой”).
- Дисперсия — ошибка, связанная с чувствительностью к малейшим флуктуациям в обучающих данных. Высокая дисперсия заставляет алгоритм моделировать случайный шум обучающих данных (также называется “чрезмерно близкой подгонкой”).
В идеале необходимо найти оптимальное значение, при котором сумма этих двух элементов будет минимальна. Это позволит добиться максимальной эффективности модели.
Примеры
Сначала рассмотрим пример недостаточно близкой подгонки.
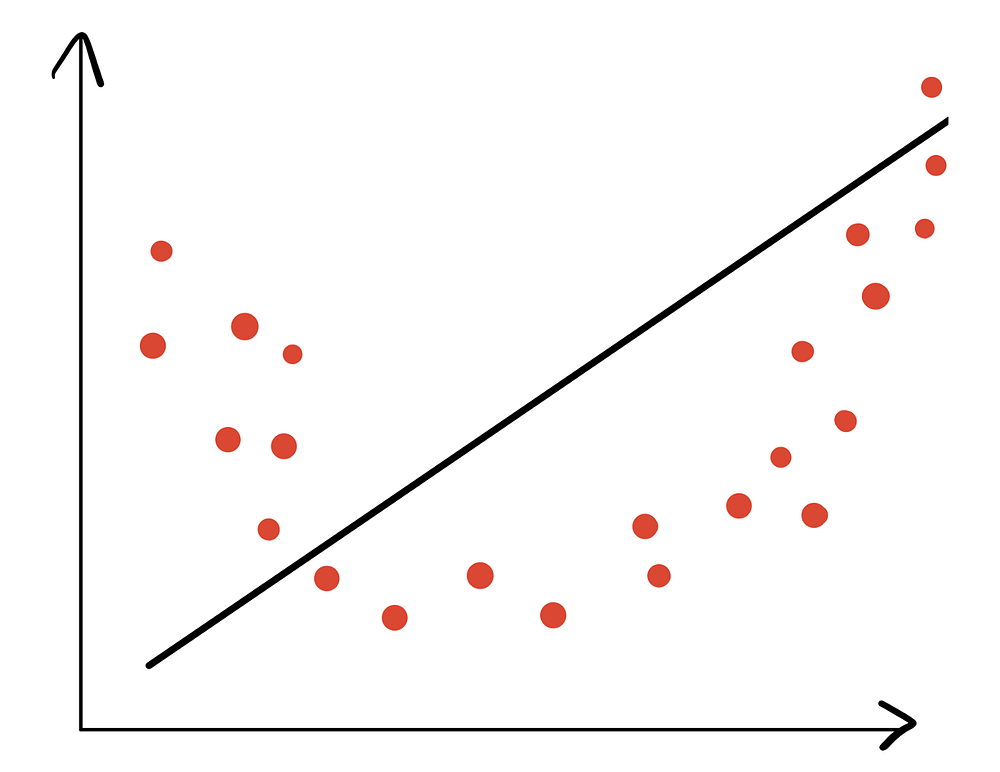
Здесь видно, что модель плохо отражает взаимосвязь между признаками и целью. Поэтому у нее высокое смещение (алгоритм упускает значимые взаимосвязи между признаками и целью), но низкая дисперсия (не моделирует случайный шум данных).
Ниже приведен пример чрезмерно близкой подгонки.

Здесь видно, что алгоритм понимает взаимосвязь между признаками и целью, но моделирует шум данных. Поэтому у него низкое смещение (алгоритм понимает взаимосвязь между признаками и целью), но высокая дисперсия (моделирует случайный шум обучающих данных).
Теперь посмотрим, как выглядит пример оптимальной подгонки.
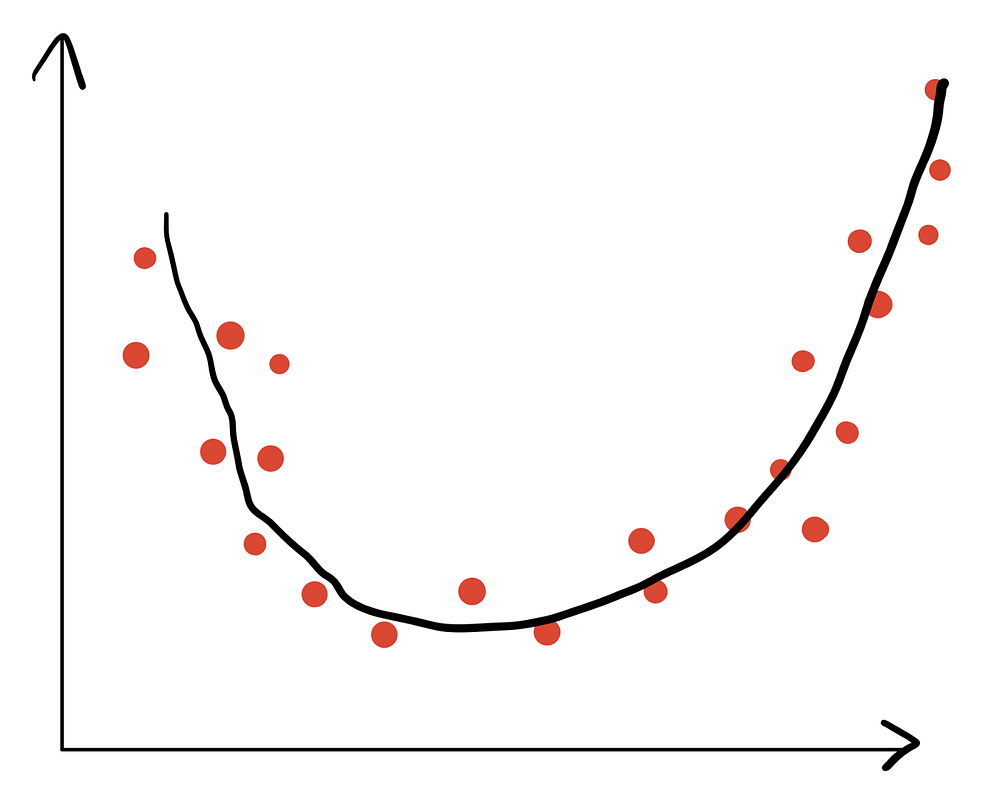
Здесь видно, что алгоритм способен установить связь между признаками и целью, но при этом не моделирует шум данных. У него низкое смещение и низкая дисперсия. Именно такой подгонки необходимо добиваться.
Связь между подгонкой и ридж-/лассо-регрессиями
При подгонке моделей линейной регрессии происходит следующее. Имея набор характеристик (обычно обозначаемых X и представленных в виде матрицы), требуется найти набор коэффициентов (обычно обозначаемых β и представленных в виде вектора), которые нужно умножить на значения X, чтобы составить целевой прогноз (обычно называемый Y и представленный в виде вектора).
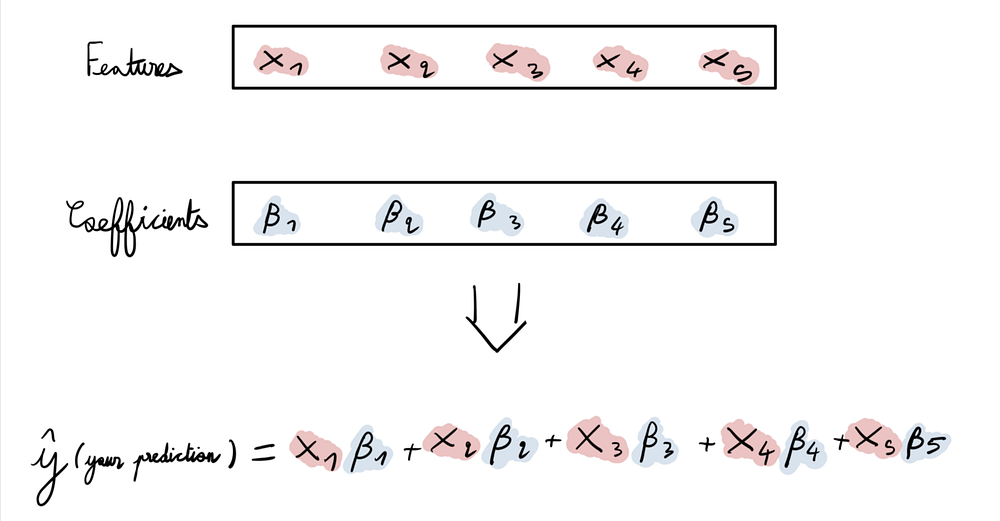
Проблема заключается в том, что в некоторых случаях линейная регрессия вызывает чрезмерно близкую подгонку определенных наборов данных. Что делать в этом случае? Использовать ридж- и лассо-регрессии.
Механизм работы ридж- и лассо-регрессий
Лассо и ридж — это модели линейной регрессии, но с поправочным (штрафным) коэффициентом, также называемым регуляризацией. Они вносят поправки в размерность бета-вектора разными способами.
Лассо-регрессия
Лассо-регрессия накладывает штраф на l1-норму бета-вектора. l1-норма вектора — это сумма абсолютных значений в этом векторе.
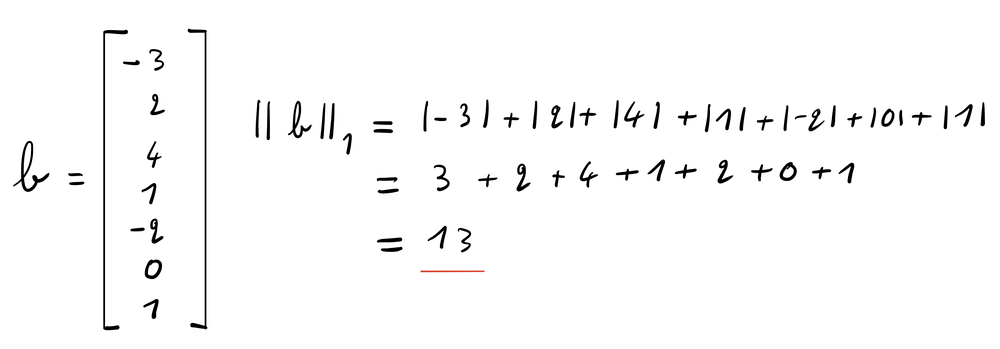
Это заставляет лассо-регрессию обнулять некоторые коэффициенты в бета-векторе. Детали этого процесса можно найти по ссылке.
Упрощенно назначение лассо-регрессии можно выразить так: “Постарайтесь достичь наилучшей производительности, но, обнаружив бесполезность некоторых коэффициентов, отбросьте их”.
Ридж-регрессия
Ридж-регрессия накладывает штраф на l2-норму бета-вектора. 2-норма вектора — это квадратный корень из суммы квадратов значений в векторе.
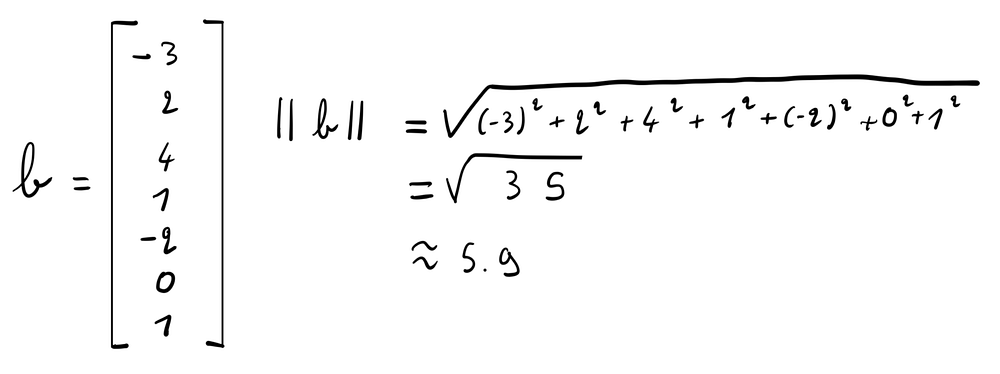
Благодаря этому, ридж-регрессия не позволяет коэффициентам бета-вектора достигать экстремальных значений (что часто происходит при чрезмерно близкой подгонке).
Простыми словами назначение ридж-регрессии можно выразить так: “Постарайтесь добиться наилучшей производительности, но ни один из коэффициентов не должен достигать экстремального значения”.
Коэффициент регуляризации
Оба эти метода имеют коэффициент регуляризации (называемый “лямбда”), который контролирует величину штрафа. При λ=0 как лассо-, так и ридж-регрессия становятся моделями линейной регрессии (в этом случае просто не накладываются никакие штрафы).
При увеличении лямбды возрастает ограничение на размер бета-вектора. При этом каждая регрессия оптимизирует его по-своему, пытаясь подобрать наилучший набор коэффициентов с учетом собственных ограничений.
Использование лассо- и ридж-регрессий (на примере набора данных Boston Housing)
Посмотрим, с какими проблемами можно столкнуться на практике и как решить их с помощью ридж- и лассо-регрессий.
Чтобы следовать руководству, перейдите по ссылке на GitHub и выполните инструкции в Readme. Набор данных можно загрузить из Kaggle.
Набор данных Boston Housing
Набор данных Boston Housing (Жилье в Бостоне) датируется 1993 годом и является одним из самых известных наборов данных в области машинного обучения. Целевым прогнозом является средняя стоимость домов в Бостоне, а характеристиками — соответствующие атрибуты дома и района.
Чтение набора данных
Первым шагом будет чтение набора данных и вывод его первых 5 строк.
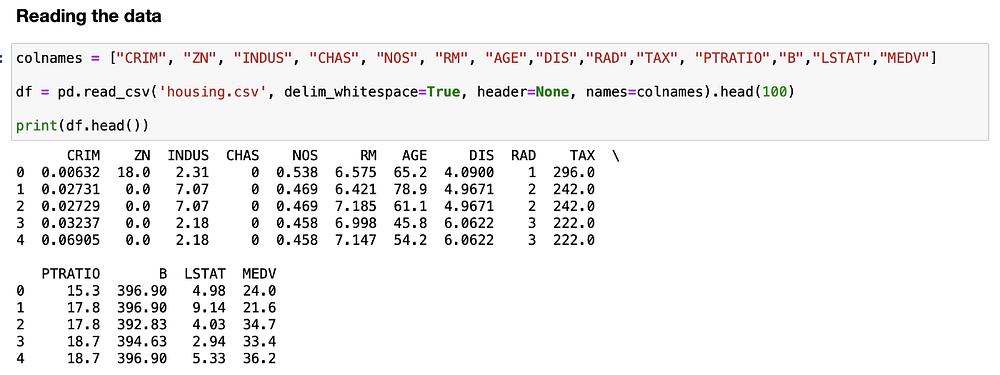
Сначала определим имена столбцов с помощью списка. Затем вызываем:
read_csvсdelim_whitespace=True, чтобы сообщить Pandas, что данные должны разделяться пробелами, а не запятыми;header=None, чтобы указать, что первая строка файла не является заголовком столбца;names=colnames, чтобы в качестве имен столбцов использовать список, определенный ранее.
Также будем использовать .head(100), чтобы сохранить только первые 100 строк набора данных, а не весь набор данных с 505 строками. Это позволит проиллюстрировать чрезмерно близкую подгонку: при меньшем набором данных она будет более очевидна. На практике сохраняйте весь набор данных (чем больше данных, тем лучше).
Разделение данных для обучения и тестирования
Следующий шаг — разделение данных на X (признаки) и Y (цель), а затем разбиение их на обучающий (X_train, y_train) и тестовый наборы (X_test, y_test). Поместим 80% данных в обучающее множество и 20% — в тестовое, что является одним из наиболее распространенных вариантов разбиения данных для задач машинного обучения.
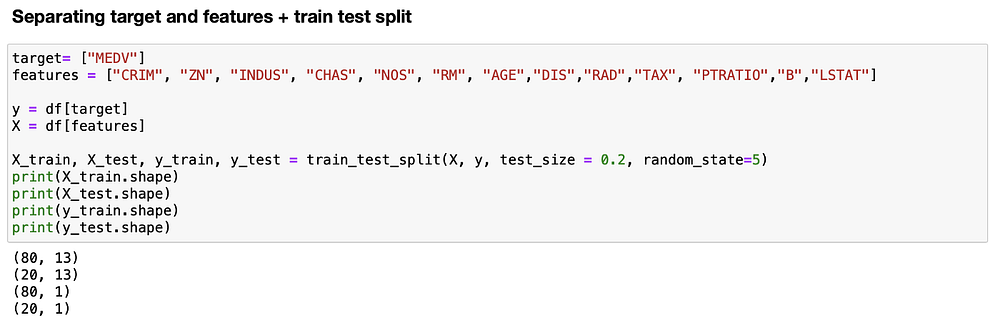
Подгонка модели линейной регрессии
После этого настраиваем модель линейной регрессии на обучающие данные и вычисляем среднюю квадратичную ошибку (MSE) на тестовых данных. Наконец, выводим бета-вектор, чтобы увидеть коэффициенты модели.
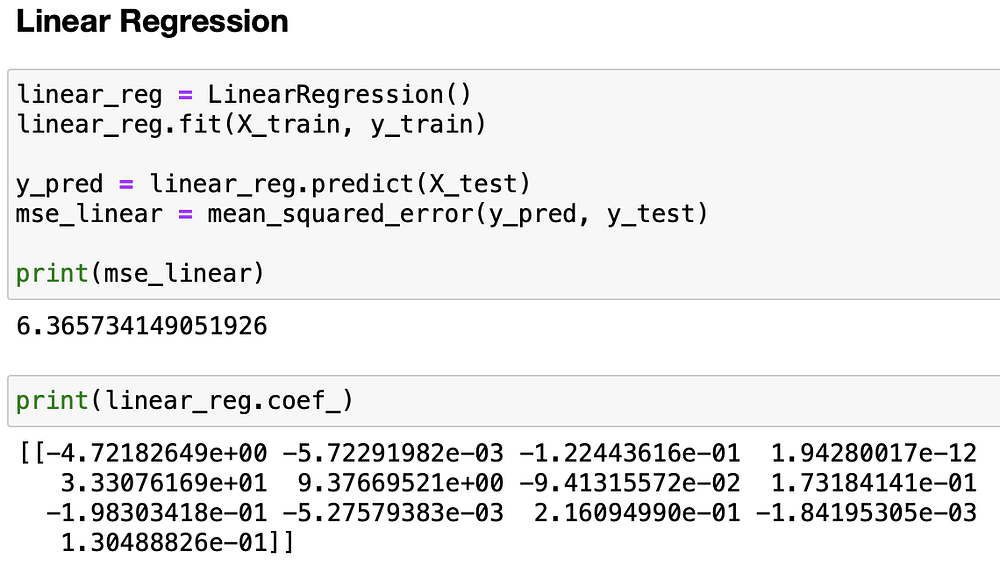
Итак, можно ли добиться большего, чем ≈6,4 MSE? Конечно, можно.
Лассо-регрессия
Теперь произведем подгонку различных моделей лассо-регрессии, используя список значений лямбды, которая является коэффициентом регуляризации (чем выше лямбда, тем больше штрафуем модель, т.е. ограничиваем сумму абсолютных значений бета-вектора).
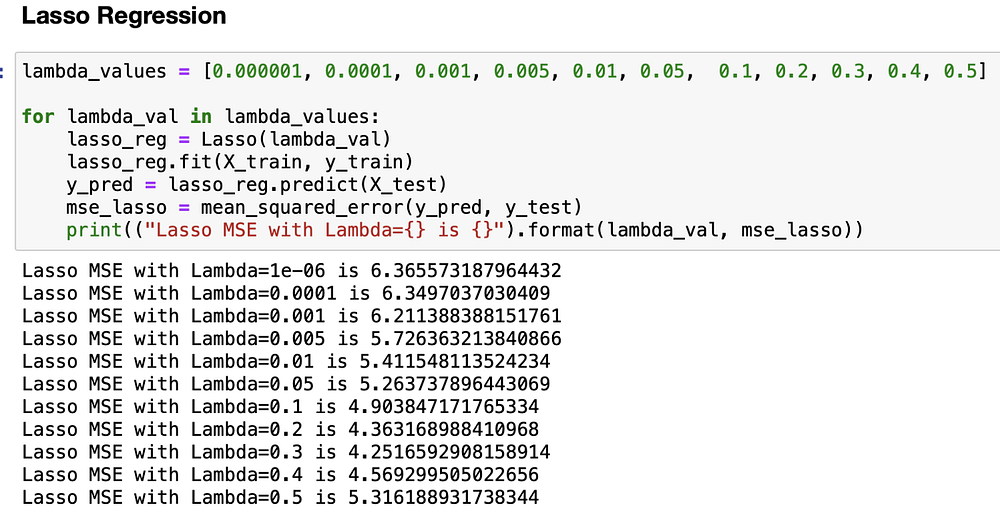
Как видите, самая высокая производительность достигается при Lambda=0,3, а MSE≈4,2. Теперь посмотрим на коэффициенты бета-вектора.

Как видите, модель обнулила около половины коэффициентов. Она оставила только 8 из 14 коэффициентов, но сохранила достаточно большой вес одного из них, RM, который представляет собой среднее количество комнат на одно жилище. Это имеет смысл, поскольку количество комнат в жилье в целом коррелирует с его ценой (квартира на 6 человек практически всегда дороже, чем квартира на 1 человека).
Таким образом, можно заметить связь с тем, что обсуждалось ранее. Мы “приказали” лассо-регрессии найти наилучшую модель, учитывая ограничения на то, какой вес можно придать каждому коэффициенту (т.е. “бюджет”). Поэтому она “решила” приложить большую часть этого “бюджета” к количеству комнат, чтобы определить цену недвижимости.
Теперь посмотрим, на что способна ридж-регрессия.
Ридж-регрессия
Проделаем те же шаги с ридж-регрессией. Значения лямбды будут разными. Следует помнить, что значения лямбды у ридж- и лассо-регрессий не пропорциональны, т.е. лямбда 5 для лассо-регрессии ни в коем случае не равна лямбде 5 для ридж-регрессии.
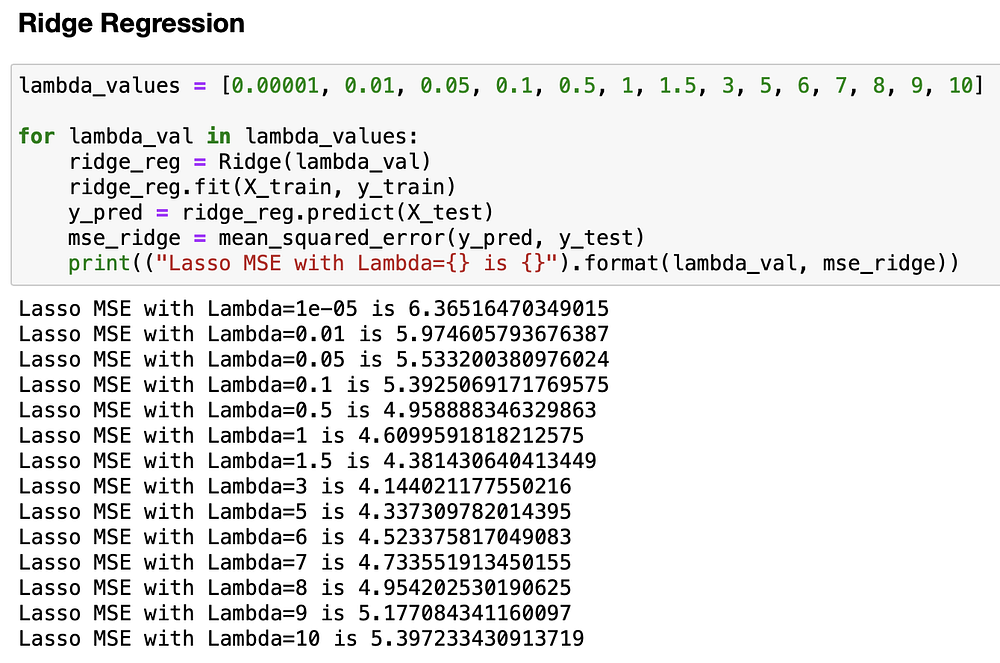
Как видно, при лямбда=3 удается добиться лучшего результата с MSE≈4,1, что лучше результата как лассо-, так и линейной регрессии. Теперь посмотрим на бета-вектор.

Как видите, коэффициент для RM все еще довольно высок (около 3,76), в то время как все остальные коэффициенты уменьшились. Однако ни один из них не был обнулен, как в случае с лассо-регрессией.
В этом заключается ключевое различие между двумя методами: лассо-регрессия часто обнуляет признаки, а ридж-регрессия уменьшает вес большинства из них в модели.
Поэтому стоит просматривать бета-векторы каждой модели и перепроверять значения: понимание того, что происходит в бета-векторе, является ключом к пониманию этих моделей.
Выбор подходящей регрессии
Лассо-регрессию следует использовать, когда есть несколько характеристик с высокой предсказательной способностью, а остальные бесполезны. Она обнуляет бесполезные характеристики и оставляет только подмножество переменных.
Ридж-регрессию лучше применять, когда предсказательная способность набора данных распределена между различными характеристиками. Ридж-регрессия не обнуляет характеристики, которые могут быть полезны при составлении прогнозов, а просто уменьшает вес большинства переменных в модели.
На практике это обычно трудно определить. Поэтому лучше всего сделать так, как описано выше, и посмотреть, какой лучший показатель MSE можно получить на тестовом множестве, используя различные значения лямбды.
Если хотите углубиться в математику (это поможет понять, как работает регуляризация), прочитайте главу 3.4 в книге “Элементы статистического обучения”, написанной Треворой Хасти, Робертом Тибширани и Джеромом Фридманом. Роберт Тибширани — автор метода лассо-регрессии. Его учебник является эталоном в этой области и позволяет углубиться в математику, одновременно давая общую картину происходящего.
Кроме того, попробуйте повторно реализовать рассмотренные методы на другом наборе данных. Посмотрите, какой из них работает лучше, и попытайтесь понять, почему.
Читайте также:
- Различные модели машинного обучения
- Инструменты для быстрого овладения наукой о данных
- Введение в метод Монте-Карло по схеме цепей Маркова
Читайте нас в Telegram, VK и Дзен
Перевод статьи Thomas Le Menestrel: Lasso and Ridge regression: An intuitive comparison






