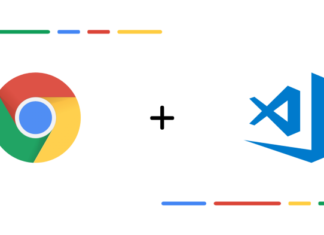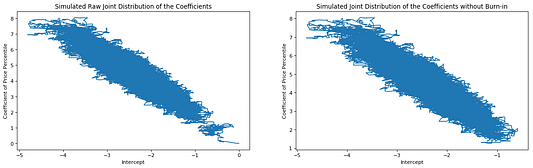
Слева: моделированное необработанное совместное распределение коэффициентов
Справа: моделированное совместное распределение коэффициентов без отбраковки
В предыдущей статье я дал краткое введение в байесовскую статистику и рассказал, как байесовский анализ объединяет априорные убеждения и экспериментальные данные, чтобы получить апостериорное распределение интересующего параметра. Задача, которую я использовал в статье, была выбрана потому, что в ней апостериорное распределение легко находится аналитически. Но, увы, чаще всего этот подход не работает, и необходимо численное решение. Алгоритм Монте-Карло по схеме цепей Маркова (Markov Chain Monte Carlo, далее MCMC) является одним из методов моделирования апостериорного распределения некоторого параметра.
Если у вас есть базовые знания байесовской статистики, смело читайте дальше. Если нет, взгляните на эту статью — в ней есть всё, что вам нужно знать, прежде чем приступить к изучению MCMC.
Алгоритм Метрополиса-Гастингса
Хорошим введением в MCMC является алгоритм Метрополиса-Гастингса. В нём 5 шагов. Давайте определим некоторые параметры и функции перед тем, как углубиться в сам алгоритм.

θ — случайный параметр, для которого моделируется распределение
Y — случайная переменная, зависящая от θ
y — реализация случайной переменной Y (выборка)
f_θ(θ) — априорное распределение (обновляющееся на каждом шаге значением предыдущего периода)
f_Y|θ(y|θ) — правдоподобие
f_θ|Y(θ|y) — апостериорное распределение
J_θ(θ|θ_t-1) — скачкообразное распределение, используемое для формирования предсказанных новых значений θ
Теперь, когда мы определили параметры, переменные и функции, пройдём по шагам алгоритм Метрополиса-Гастингса.

Шаг 1:
Выбираем начальное значение: θ_t-1. При t = 1, θ_t-1 — наше начальное априорное значение для θ.
Шаг 2:
Формируем предсказание для периода t - θ*_t - путём выборки из скачкообразного распределения J(θ|θ_t-1). Метод Монте-Карло в MCMC проявляется в том, что случайное число моделируется из скачкообразного распределения. Цепи Маркова проявляются в том, что θ*_t зависит только от значения θ_t-1. Процесс “не обладает памятью”, следовательно является цепью Маркова.

Шаг 3
Находим отношение апостериорного предсказания к апостериорному распределению априорного значения.
Затем перегруппируем для симметричных скачкообразных значений.

Шаг 4
Формируем случайное число a, принадлежащее к равномерному непрерывному распределению(0,1).
Если r > a, θ_t = θ*_t (мы принимаем предполагаемое значение). Вероятность min(r, 1).
Если r ≤ a, θ_t = θ_t-1 (мы отвергаем предсказанное значение и используем априорное значение). Вероятность 1 — min(r, 1).
Если r ≥ 1 (θ*_t более вероятно, чем θ_t-1), всегда будет принято. Иногда мы принимаем θ*_t, потому что не хотим попасть в ловушку в локальном минимуме.
Шаг 5
Повторяем, пока не достигнем максимального количества итераций.
Не так уж и страшно, когда вы знаете, как это работает, верно?
Обычно в качестве скачкообразного распределения используется нормальное распределение, потому что центрированное в 0 оно может создавать предсказания как меньшие, так и большие относительно предыдущего предсказания. Среднеквадратичное отклонение скачкообразного распределения является важным параметром настройки. Если априорное распределение находится далеко от области плотности апостериорного распределения на числовой оси, а среднеквадратичное отклонение скачкообразного распределения невелико, пройдёт немало времени, прежде чем у вас получится формировать предсказания из верной области числовой оси. Если среднеквадратичное отклонение скачкообразного распределения слишком велико по отношению к реальному распределению параметра, в моделированном апостериорном распределении будет много пробелов, потому что в этих областях не сформировано ни одного предсказания. К счастью, пакеты для MCMC содержат адаптивные среднеквадратичные отклонениях для скачкообразных распределений, поэтому на практике вы можете не беспокоиться по поводу этого параметра.
После формирования апостериорного распределения стандартной практикой является отбраковка области. Это связано с тем, что алгоритму может потребоваться слишком много итераций для поиска вероятных значений в пространстве параметров. Чтобы использовать 10% отбраковки, просто отбросьте первые 10% моделированных значений. После удаления отбракованной части получим моделированное апостериорное распределение, которое можно использовать для байесовского вывода — построения байесовских доверительных интервалов.
Применение модифицированного алгоритма Метрополиса-Гастингса к логистической регрессии
Теперь, когда мы поняли алгоритм Метрополиса-Гастингса, мы можем модифицировать его, чтобы он соответствовал коэффициентам логистической регрессионной модели. Расчётными параметрами будут 𝛽𝑗 для 𝑗=1,2,…𝑘, где 𝑘 — число коэффициентов в модели. Основное отличие состоит в том, что вместо одного параметра будут рассчитываться несколько. Я справился с этим, формируя предсказание для каждого 𝛽𝑗 каждого цикла, при этом рандомизируя порядок каждого цикла 𝛽𝑗.
Чтобы построить алгоритм MCMC для логистической регрессионной модели, нужно определить 4 функции. Это позволит нам вычислить соотношение апостериорных распределений для предсказанных 𝛽𝑗 на каждом шаге алгоритма MCMC.
Первая функция
inv_logit, отменяющая логит-преобразование. Логит-преобразование превращает вероятность в логит-функцию.
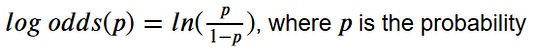
Выходные данные логистической регрессии представлены в формате логит-функции. Функция inv_logit нужна нам для переложения логит-функции в вероятности при расчёте логарифмического правдоподобия для вектора 𝛽 с учётом данных.
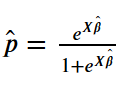
Вторая функция
normal_log_prior, вычисляющая логарифм априорного распределения вектора 𝛽 с учётом априорных убеждений о математических ожиданиях и среднеквадратичных отклонениях отдельных 𝛽𝑗. Это натуральный логарифм плотности многомерного нормального распределения, где каждый элемент равен 𝑁∼(априорное математическое ожидание j, априорное среднеквадратичное отклонение j) при 𝛽. Натуральный логарифм используется для предотвращения исчезновения значащих разрядов.
Третья функция
log_likelihood, вычисляющая логарифм правдоподобия вектора 𝛽 с учётом данных. Поскольку мы моделируем задачу второго класса с помощью логистической регрессии, вероятность однократного наблюдения вычисляется по формуле Бернулли:
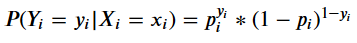
Правдоподобие вектора 𝛽 с учётом данных является произведением отдельных вероятностей Бернулли.
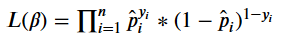
Следовательно, логарифмическое правдоподобие:
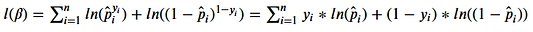
Натуральный логарифм используется для предотвращения исчезновения значащих разрядов.
Четвёртая функция
log_posterior рассчитывает апостериорное распределение вектора 𝛽 с учётом данных и наших априорных убеждений. апостериорное распределение ∝ априорное распределение∗правдоподобие, таким образом 𝑙𝑛(апостериорного распределения) ∝ 𝑙𝑛(априорного распределения)+𝑙𝑛(правдоподобие).
Определив эти функции, я смог реализовать модифицированный алгоритм Метрополиса-Гастингса. Кроме того, я добавил функции для удаления отбракованной области, вычисления байесовских доверительных интервалов и прогнозирования. Чтобы сделать прогноз, пользователь должен указать, хочет ли он использовать среднее значение выборки, математическое ожидание или модальное значение моделированных апостериоров для каждого 𝛽𝑗 в качестве коэффициентов при вычислении 𝛽.
class mcmc_logistic_reg:
import numpy as np
def __init__self(self):
self.raw_beta_distr = np.empty(1)
self.beta_distr = np.empty(1)
self.beta_hat = np.empty(1)
self.cred_ints = np.empty(1)
def inv_logit(self, beta, X):
###
# Функция для отмены логит-преобразования. Переложение
# логит-функции в вероятности.
###
return (np.exp(np.matmul(X, beta.reshape((-1, 1)))) /
(1 + np.exp(np.matmul(X, beta.reshape((-1, 1))))))
def normal_log_prior(self, beta, prior_means, prior_stds):
###
# Функция для вычисления логарифма априорного распределения
# с помощью нормального распределения.
# Используется для предотвращения исчезновения значащих
# разрядов.
###
from scipy.stats import norm
import numpy as np
return np.sum(norm.logpdf(beta, loc=prior_means.reshape((-1,
1)), scale=prior_stds.reshape((-1, 1))))
def log_likelihood(self, y, X, beta):
###
# Определяет функцию для вычисления логарифмического
# правдоподобия beta с учётом данных.
# Использует логарифмическое правдоподобие вместо
# нормального правдоподобия, чтобы избежать исчезновения
# значащих разрядов.
###
return np.sum(y * np.log(self.inv_logit(beta.reshape((-1,
1)), X)) +
(1-y)*np.log((1-self.inv_logit(beta.reshape((-1,1)),X))))
def log_posterior(self, y, X, beta, prior_means, prior_sds):
###
# Определяет функцию для вычисления логарифма апостериорного
# значения beta с учётом логарифмического правдоподобия и
# логарифма априорных значений, предполагая, что это
# нормальное априорное значение.
###
return (self.normal_log_prior(beta, prior_means, prior_stds)
+ self.log_likelihood(y, X, beta))
def mcmc_solver(self,
y,
X,
beta_priors,
prior_stds,
jumper_stds,
num_iter,
add_intercept,
random_seed):
from scipy.stats import norm
from tqdm import tqdm
# устанавливаем случайное начальное число
np.random.seed(random_seed)
# при желании добавляем выделение отрезка
if add_intercept:
X_mod = np.append(np.ones(shape=(X.shape[0], 1)),X, 1)
else:
X_mod = X
# создаём список beta-индексов, зацикленных внутри
# каждой итерации
beta_indexes = [k for k in range(len(beta_priors))]
###
# Инициализируем beta_hat с априорными значениями. Число
# строк будет равно числу beta-коэффициентов, а число
# столбцов - числу итераций для априорного значения + 1.
# Каждая строка будет содержать значения для одного
# коэффициента. Каждая строка - итерация алгоритма.
###
beta_hat = np.array(np.repeat(beta_priors, num_iter+1))
beta_hat = beta_hat.reshape((beta_priors.shape[0],
num_iter+1))
# выполняем num_iter итерации
for i in tqdm(range(1, num_iter + 1)):
# перемешиваем beta-индексы, чтобы порядок коэффициентов
# выполняющих шаги Метрополиса, был случайным
np.random.shuffle(beta_indexes)
# последовательно делаем выборку для каждой beta_hat
for j in beta_indexes:
# формируем предсказание beta, используя нормальное
# распределение и beta_j
proposal_beta_j = beta_hat[j, i-1] +
norm.rvs(loc=0, scale=jumper_stds[j],size=1)
# получаем один вектор для всех самых последних beta
beta_now = beta_hat[:, i-1].reshape((-1, 1))
# копируем текущий вектор beta и вставляем в
# предсказанный beta_j в j-м индексе
beta_prop = np.copy(beta_now)
beta_prop[j, 0] = proposal_beta_j
# вычисляем апостериорную вероятность предсказанного
# значения beta
log_p_proposal = self.log_posterior(y, X_mod,
beta_prop,
beta_now,
prior_stds)
# вычисляем апостериорную вероятность текущего
# значения beta
log_p_previous = self.log_posterior(y, X_mod,
beta_now,
beta_now,
prior_stds)
# вычисляем логарифм r-соотношения
log_r = log_p_proposal - log_p_previous
# если r больше случайного значения из равномерного
# распределения(0, 1), добавляем предсказанное
# beta_j в список всех beta_j
if np.log(np.random.random()) < log_r:
beta_hat[j, i] = proposal_beta_j
# в противном случае просто добавляем прежнее
# значение
else:
beta_hat[j, i] = beta_hat[j, i-1]
# задаём атрибут raw_beta_distr матрицы beta_hat
self.raw_beta_distr = beta_hat
def trim(self, burn_in):
###
# Эта функция обрезает распределение всех beta_hat на основе
# размера отбраковки
###
start = 1 +
round(burn_in * self.raw_beta_distr.shape[1] - 1)
# задаём атрибут beta_distr для raw_beta_distr минус
# отбраковка
self.beta_distr = self.raw_beta_distr[:, start:-1]
def credible_int(self, alpha=0.05):
###
# Возвращает 100*(1-alpha)% байесовский доверительный
# интервал для каждого коэффициента в массиве 2 по
# количеству коэффициентов массива numpy
###
from numpy import transpose, quantile
self.cred_ints = transpose(quantile(self.beta_distr,
q=(alpha/2, 1-alpha/2),
axis=1))
def fit(self, method = 'median'):
###
# Использует распределение betas_hat без отбраковки, чтобы
# выдать либо среднее значение выборки, либо математическое
# ожидание, либо модальное значение в качестве возможного
# значения вектора beta
###
from numpy import median, mean
from scipy.stats import mode
if method == 'median':
beta_hat = median(self.beta_distr, axis=1).reshape((-1,1))
elif method == 'mean':
beta_hat = mean(self.beta_distr, axis=1).reshape((-1,1))
else:
beta_hat = mode(self.beta_distr, axis=1)[0]
# задаёт в качестве атрибута beta_hat среднее значение
# выборки, математическое ожидание или модальное
# значение
self.beta_hat = beta_hat
def predict(self, X_new, add_intercept=True, prob=True):
###
# Выдаёт предсказания в виде лог-функции или вероятностей
# (по умолчанию)
###
from numpy import matmul
# добавляет разделительный столбец (по желанию)
if add_intercept:
X_mod = np.append(np.ones(shape=(X_new.shape[0],
1)),X_new, 1)
else:
X_mod = X_new
# выдаёт значение предсказанных вероятностей, если
# prob == True
if prob:
predictions = self.inv_logit(self.beta_hat, X_mod)
# в противном случае выдаёт предсказанную лог-функцию
else:
predictions = matmul(X_mod, self.beta_hat)
# возвращает предсказания
return predictions
def predict_class(self, X_new, add_intercept=True, boundary=0.5):
###
# предсказывает класс новых наблюдений, основываясь на
# решающей границе для вероятности. Если предсказанная
# вероятность > границы, она принадлежит классу 1
###
from numpy import where
# предсказываем вероятности
preds = self.predict(X_new, add_intercept, prob=True)
# устанавливаем предсказанное значение на 1 или 0 на основе
# границы
pred_classes = where(preds > boundary, 1, 0)
return pred_classesПосле определения класса протестируем его на реальных данных.
Применение MCMC логистической регрессии к реальным данным
Чтобы протестировать модель логистической регрессии MCMC, я использовал этот набор данных, содержащий данные о 86 сладостях. Я выбрал простую модель, содержащую выделение отрезка на оси и “процент цены” (“Процентиль цены за единицу товара в сравнении с остальными товарами в наборе.”), для предсказания вероятности того, что сладость окажется шоколадкой.
Вот модель:
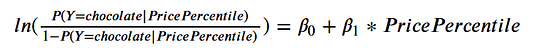
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# загружаем данные
all_data = pd.read_csv('candy-data.csv')
# список независимых переменных модели
vars_of_interest = ['pricepercent']
# имя зависимой переменной
target = 'chocolate'
my_data = all_data[[target] + vars_of_interest]
my_data = all_data.dropna()
# создаём столбцы-векторы массива numpy для зависимой переменной
y = np.array(my_data[target]).reshape((-1,1))
# создаём столбцы-векторы массива numpy для независимой переменной
X = np.array(my_data[vars_of_interest]).reshape((-1,len(vars_of_interest)))
# создаём столбцы-векторы массива numpy для априорных математических
# ожиданий выборки beta
beta_priors = np.repeat(0.0, len(vars_of_interest)+1)
# создаём столбцы-векторы массива numpy для априорных
# среднеквадратичных отклонений beta
betaprior_stds = np.repeat(1, len(vars_of_interest))
# создаём строки-векторы массива numpy для среднеквадратичного
# отклонения скачкообразного распределения
jumper_stds = np.repeat(0.1, len(vars_of_interest)+1)
# задаём число итераций
num_iter = 50000
# задаём размер отбраковки
burn_in = 0.1
# задаём alpha для байесовского доверительного интервала
cred_int_alpha = 0.05
# задаём значение true для добавления выделения отрезка на оси к
# данным
add_intercept = True
# задаём случайное начальное число
random_seed = 1
# задаём решающие границы для классов
boundary = 0.5
# создаём инстанс mcmc_logistic_reg
mcmc_log_mod = mcmc_logistic_reg()
# создаём неограниченное распределение значений beta_hat
mcmc_log_mod.mcmc_solver(y,
X,
beta_priors,
prior_stds,
jumper_stds,
num_iter,
add_intercept,
random_seed)
# создаём распределение значений beta_hat без отбраковки
mcmc_log_mod.trim(burn_in)
# используем среднее значение выборки распределений beta_hat в
# качестве коэффициентов для предсказания
mcmc_log_mod.fit(method='median')
# создаём байесовские доверительные интервалы для
mcmc_log_mod.credible_int(cred_int_alpha)
plt.figure(figsize=(12, 5), dpi= 80, facecolor='w', edgecolor='k')
plt.subplot(1, 2, 1)
plt.plot(mcmc_log_mod.raw_beta_distr[0], mcmc_log_mod.raw_beta_distr[1])
plt.title('Simulated Raw Joint Distribution of the Coefficients', fontsize=12)
plt.xlabel('Intercept', fontsize=10)
plt.ylabel('Coefficient of Price Percentile', fontsize=10)
plt.subplot(1, 2, 2)
plt.plot(mcmc_log_mod.beta_distr[0], mcmc_log_mod.beta_distr[1])
plt.title('Simulated Joint Distribution of the Coefficients without Burn-in', fontsize=12)
plt.xlabel('Intercept', fontsize=10)
plt.ylabel('Coefficient of Price Percentile', fontsize=10)
plt.show();
plt.figure(figsize=(12, 5), dpi= 80, facecolor='w', edgecolor='k')
plt.subplot(1, 2, 1)
plt.hist(mcmc_log_mod.beta_distr[0], density=True)
plt.title(f'Simulated Distr. of Intercept with {100 * (1-cred_int_alpha)}% Cred. Int.',
fontsize=12)
plt.xlabel('Intercept', fontsize=10)
plt.ylabel('Density', fontsize=10)
plt.axvline(x=mcmc_log_mod.cred_ints[0,0], color='r', linestyle='dashed', linewidth=2)
plt.axvline(x=mcmc_log_mod.cred_ints[0,1], color='r', linestyle='dashed', linewidth=2)
plt.subplot(1, 2, 2)
plt.hist(mcmc_log_mod.beta_distr[1], density=True)
plt.title(f'Simulated Distr. of Price Percentile Coef. with {int(100 * (1-cred_int_alpha))}% Cred. Int.',
fontsize=12)
plt.xlabel('Price Percentile Coefficient', fontsize=10)
plt.ylabel('Density', fontsize=10)
plt.axvline(x=mcmc_log_mod.cred_ints[1,0], color='r', linestyle='dashed', linewidth=2)
plt.axvline(x=mcmc_log_mod.cred_ints[1,1], color='r', linestyle='dashed', linewidth=2)
plt.show();
# проводим линию регрессии
x_ = np.arange(my_data[vars_of_interest[0]].min(),
my_data[vars_of_interest[0]].max(),
step=0.01)
x_ = x_.reshape((-1, 1))
y_ = mcmc_log_mod.predict(x_)
plt.figure(figsize=(12, 5), dpi= 80, facecolor='w', edgecolor='k')
plt.plot(x_, y_, '-', color='r')
plt.scatter(X, y)
plt.hlines(xmin=x_[0], xmax=x_[-1], y=boundary, color='g', linestyle='dashed', linewidth=2)
plt.title('Price Percentile vs. Probability of Being Chocolate', fontsize=15)
plt.xlabel('Price Percentile', fontsize=15)
plt.ylabel('Probability of Being Chocolate', fontsize=15)
plt.show;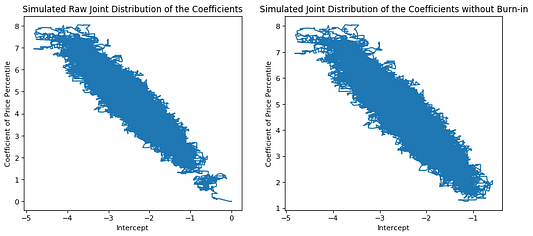
Как видите, моделированное совместное распределение 𝛽0 и 𝛽1 формирует эллиптическую область (как и совместные распределения в обобщённых линейных моделях). На графике совместного распределения с отбраковкой коэффициенты “идут” от начала координат, немного проходят по кругу и затем достигают эллиптической области. Эти коэффициенты, идущие от априорных значений в эллиптическую область, мы можем определить как “истинное” моделированное совместное распределение.
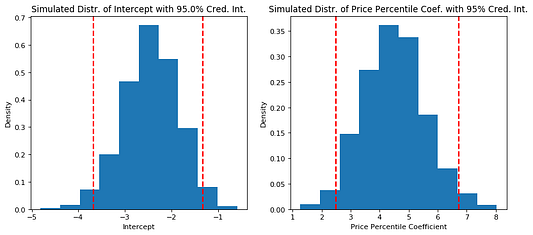
В 95% случаев байесовский доверительный интервал для 𝛽0 равен [-3,67; -1,32], а для 𝛽1 равен [2,50; 6,72]. Моделированное среднее значение выборки 𝛽0 равно -2,44, выборки 𝛽1 — 4,48. Более высокая цена положительно влияет на вероятность того, что сладость окажется шоколадом.
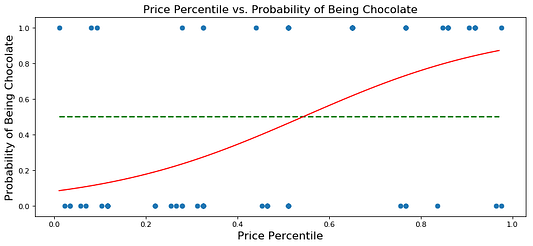
Сравнивая графики процентиля цены и вероятности оказаться шоколадом, видим, что модель имеет красивую S-образную форму, демонстрируемую в учебниках по логистической регрессии. Не похоже, что она проделывает отличную работу по классификации сладости как шоколада (слишком много ложных негативных значений в сравнении с истинными положительными), поэтому, вероятно, нужна более сложная модель.*
*Безусловно стоит использовать проверки и тестовые наборы данных для оценки производительности модели при построении реальных прогнозирующих моделей. Процесс обучения, проверки и тестирование выходят за рамки этой статьи. Здесь мы рассматриваем только применение MCMC.
Сравниваем с логистической регрессией, рассчитанной с помощью оценки максимального правдоподобия
Теперь, когда мы настроили совместную работу логистической регрессии и модифицированного алгоритма Метрополиса-Гастингса, сравним результаты со стандартной оценкой максимального правдоподобия (ОМП). Результаты очень похожи!
from statsmodels.discrete.discrete_model import Logit
# добавляем выделение отрезка на оси, так как статистический модуль
# этого не делает
my_data['Intercept'] = 1
# логистическая регрессия с использованием ОМП
mle_mod = Logit(my_data[target], my_data[['Intercept'] + vars_of_interest])
mle_mod_fit = mle_mod.fit(disp=False)
# печатаем
print(mle_mod_fit.summary())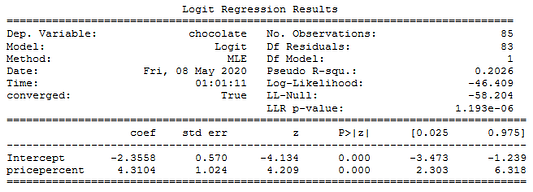
Если я всё сделал верно, вы поняли идею MCMC, в частности, алгоритм Метрополиса-Гастингса, а также применение к таким практическим задачам, как подбор логистической регрессионной модели.
Спасибо! Если вы интересуетесь MCMC, байесовским статистическим моделированием и машинным обучением, взгляните на pymc3.
Репозиторий для этого проекта можно найти здесь.
Читайте также:
- Байесовская статистика для специалистов по данным
- Распознавание звуков с помощью глубокого обучения
- В США ограничивают использование технологий распознавания лиц
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи John Clements: Intro to Markov Chain Monte Carlo