Представьте, что вы играете в стратегию. У вас есть:
- три вида ресурсов (еда, дерево и золото);
- три вида юнитов (мечники, лучники и наездники).
Наездники сильнее лучников, которые, в свою очередь, сильнее мечников. В следующей таблице приведена информация о силе и стоимости каждого юнита:
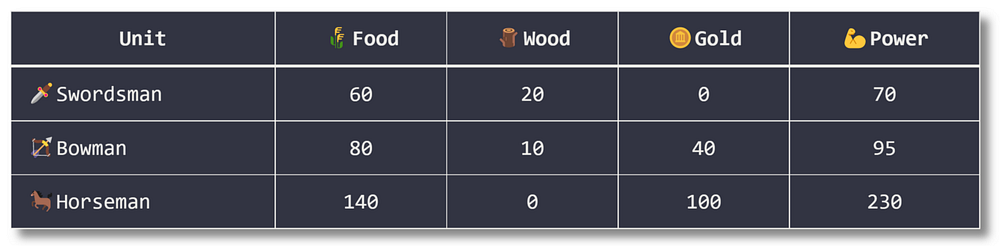
Итак, у вас есть 1200 еды, 800 дерева и 600 золота. Как с помощью этих ресурсов максимизировать силу армии?
Можно просто найти юнит с наилучшим соотношением силы/стоимости, приобрести их как можно больше, а затем повторить процесс с оставшимися двумя. Но подход “угадай и проверь” может даже не быть оптимальным.
Теперь представьте, что у вас миллионы юнитов и ресурсов. Предыдущая стратегия, скорее всего, не приведет к наилучшему варианту. Для решения этой задачи возможно применение алгоритма машинного обучения (например, генетический алгоритм), но, как и в первом случае, нет гарантии на оптимальный результат.
К счастью, существует метод, который решит эту задачу наилучшим образом, — линейное программирование (или линейная оптимизация), входящее в область исследования операций. Сегодня мы будем использовать этот метод для определения лучшего количества мечников, лучников и наездников с целью создания армии с максимально возможной силой.
1. Решатели (солверы)
Для линейного программирования в Python существуют разные библиотеки — многоцелевая SciPY, удобная для новичков PuLP, всеохватывающая Pyomo и многие другие.
Сегодня мы воспользуемся инструментом Google OR-Tools, который поставляется c несколькими готовыми решателями и имеет наибольшее количество звезд на GitHub. Вы можете запустить код из этого руководства, используя блокнот Google Colab.
Если установка не прошла, перезапустите ядро и попробуйте снова: иногда случаются неполадки.
!python -m pip install --upgrade --user -q ortools
Все эти библиотеки имеют скрытое преимущество: они выступают в роли интерфейсов, чтобы использовать одну модель с разными решателями. Такие солверы, как Gurobi, Cplex и SCIP, имеют собственные API, но модели, которые они создают, привязаны к конкретному решателю.
OR-Tools позволяет использовать абстрактный путь моделирования задачи. Затем мы можем выбрать один или несколько решателей для поиска оптимального варианта. Таким образом, созданную модель можно использовать многократно!
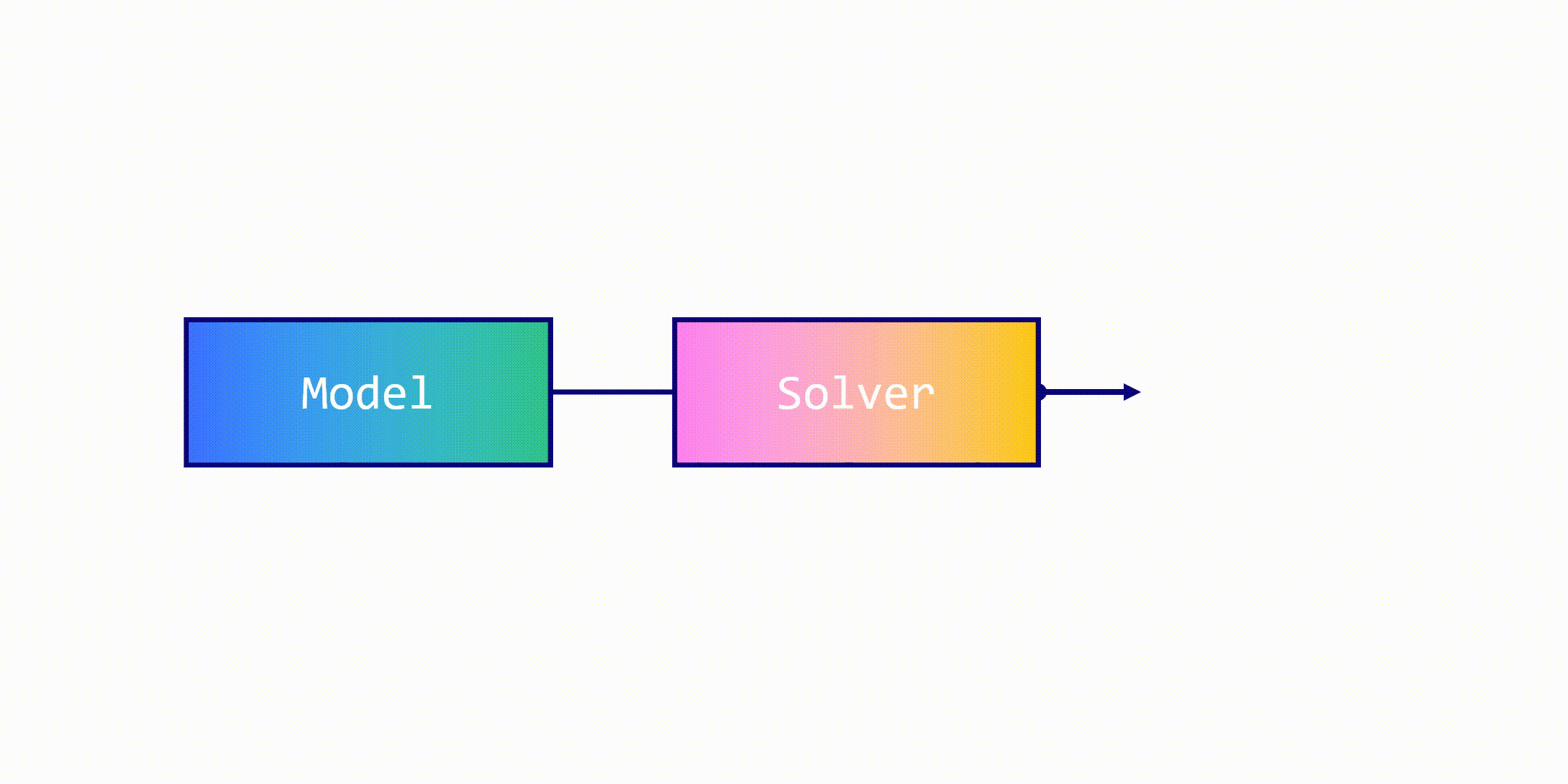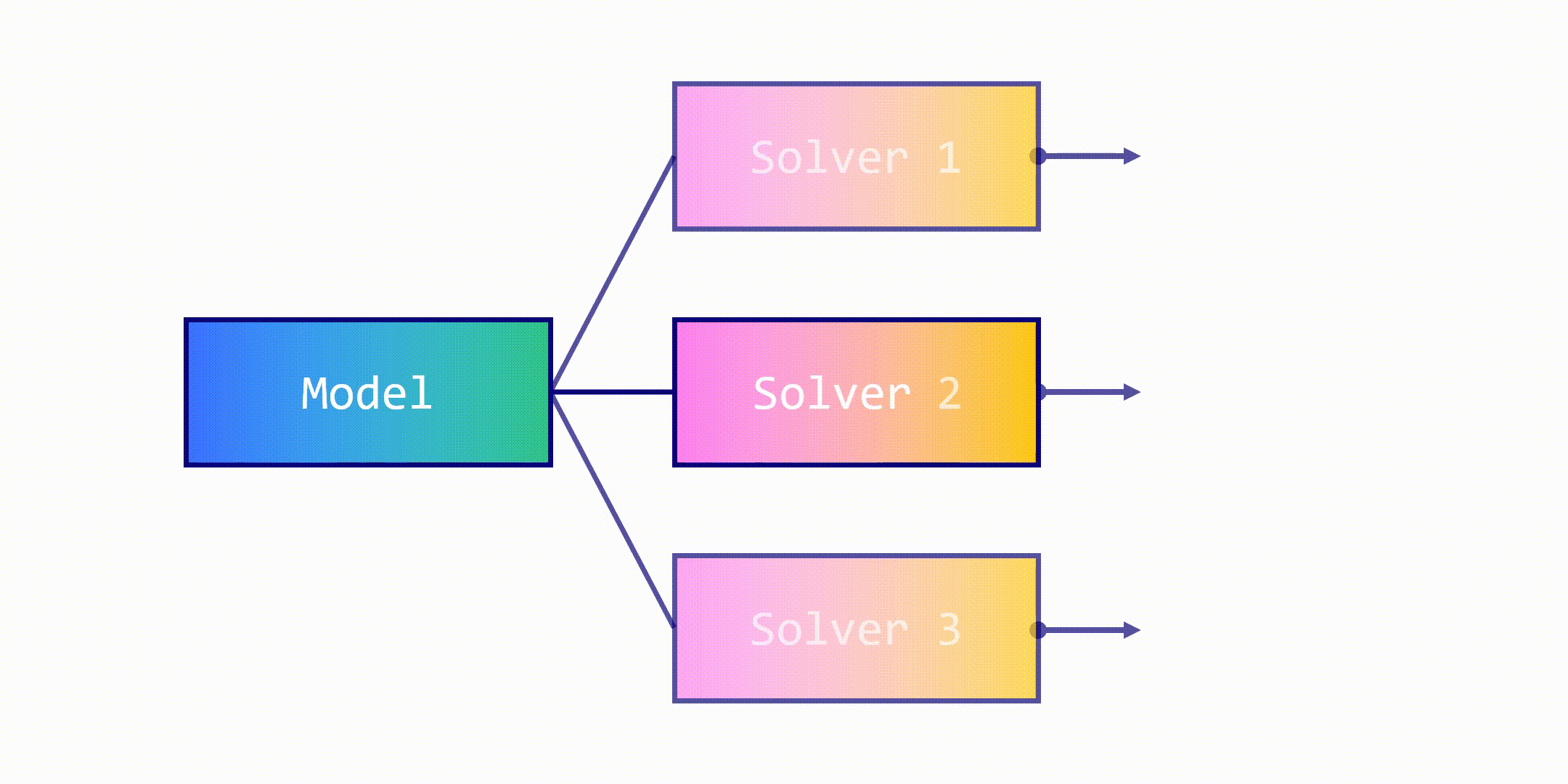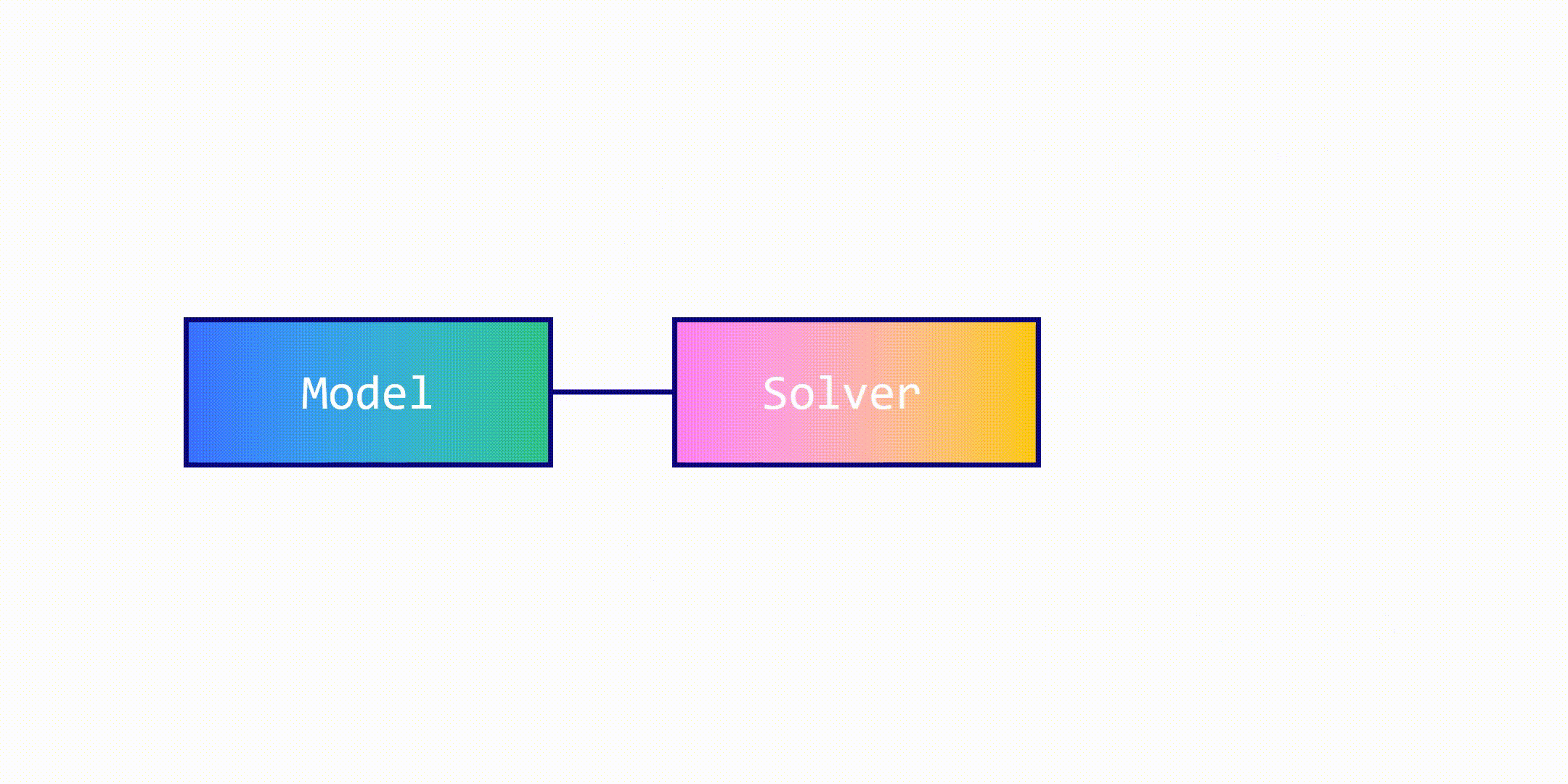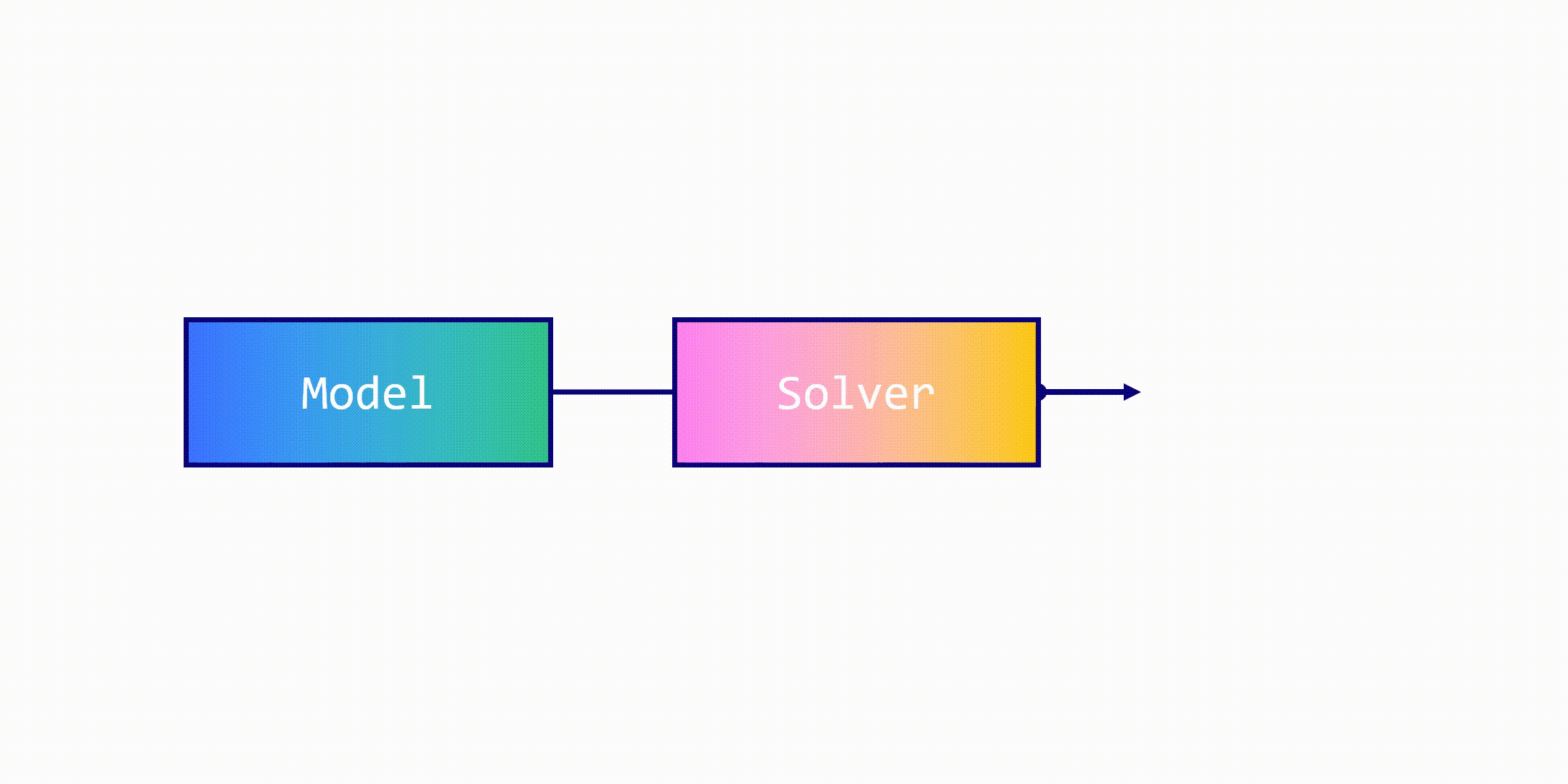
Google OR-Tools имеет собственный решатель линейного программирования под названием GLOP (Google Linear Optimization Package). Это проект с открытым исходным кодом, созданный командой Google по исследованию операций и написанный на С++.
Также доступен SCIP — некоммерческий решатель, созданный в 2005 году и получающий обновления и поддержку по сей день. Как вариант, можно использовать коммерческие версии типа Gurobi и Cplex. Однако вам придется установить их поверх OR-Tools и получить соответствующую лицензию (что может стоить дорого). Для начала попробуем GLOP.
# Импортируем оболочку OR-Tools для линейного программирования
from ortools.linear_solver import pywraplp
# Создаем решатель с помощью бэкенда GLOP
solver = pywraplp.Solver('Maximize army power', pywraplp.Solver.GLOP_LINEAR_PROGRAMMING)
2. Переменные
Мы создали копию решателя OR-Tools с помощью GLOP. Как же использовать линейное программирование? Первым делом необходимо определить переменные, которые нужно оптимизировать.
В данном примере имеется три значения: количество мечников, лучников и наездников в армии. OR-Tools принимает три типа переменных:
NumVarдля непрерывных переменных;IntVarдля целочисленных переменных;BoolVarдля булевских переменных.
Нам нужно круглое число юнитов в армии, поэтому выбираем IntVar. Затем нужно определиться с нижними и верхними границами этих переменных. Как минимум необходимо 0 юнитов, но верхней границы по количеству нет, поэтому можно сказать, что она бесконечна (или имеет большое значение, которого никогда не достигнуть). Записать это можно так:

Переведите это в код. Бесконечность заменяем на solver.infinity() в OR-Tools. В остальном синтаксис довольно прост:
# Создаем переменные для оптимизации
swordsmen = solver.IntVar(0, solver.infinity(), 'swordsmen')
bowmen = solver.IntVar(0, solver.infinity(), 'bowmen')
horsemen = solver.IntVar(0, solver.infinity(), 'horsemen')
3. Ограничения
Переменные определены, но ограничения не менее важны.
Как бы парадоксально это не звучало, но добавление большего количества ограничений помогает решателю быстрее находить оптимальное решение. В чем же дело? Солвер можно сравнить с деревом: ограничения помогают ему обрезать ветки и уменьшать область поиска.
В данном случае имеется ограниченное количество ресурсов для производства юнитов. Иначе говоря, мы не можем потратить больше, чем у нас есть. Например, количество еды для найма юнитов не может превышать 1200. То же самое относится к лесу (800) и золоту (600).
Согласно таблице, у юнитов следующая стоимость:
- 1 мечник = 60 (еда)+ 20 (лес);
- 1 лучник = 80 (еда) + 10 (лес) + 40 (золото);
- 1 наездник = 140 (еда) + 100 (золото).
Можно написать одно ограничение на каждый ресурс, как показано ниже:

В OR-Tools просто добавляем ограничения в копию решателя с solver.Add().
4. Цель
Теперь, имея переменные и ограничения, необходимо определить цель (или целевую функцию).
В линейном программировании эта функция должна быть линейной (как и ограничения), то есть иметь вид ax + by + cz + d. В данном примере цель вполне ясна — необходимо собрать армию с максимальным показателем силы. Таблица дает следующие значения силы:
- 1 мечник = 70;
- 1 лучник = 95;
- 1 наездник = 230.
Максимизация силы армии равна максимизации суммы силы каждого юнита. Целевая функция может выглядеть так:

В целом, у целевой функции есть только два типа: максимизация или минимизация. В OR-Tools мы указываем это с помощью solver.Maximize() и solver.Minimize().
solver.Maximize(swordsmen*70 + bowmen*95 + horsemen*230
Готово! Чтобы смоделировать любую задачу линейной оптимизации, нужно выполнить три шага.
- Указать переменные для оптимизации с нижними и верхними границами.
- Добавить ограничения к этим переменным.
- Определить целевую функцию для максимизации или минимизации.
С этим разобрались, теперь можно попросить солвер найти оптимальное решение.
5. Оптимизация!
Расчет наилучшего варианта закончен с помощью solver.Solve() . Эта функция возвращает статус, который можно использовать, чтобы проверить оптимальность принятого решения.
Выведем наибольшую суммарную силу, которую можно получить с наилучшим составом армии:
status = solver.Solve()
# Если оптимальное решение найдено, вывести результаты
if status == pywraplp.Solver.OPTIMAL:
print('================= Solution =================')
print(f'Solved in {solver.wall_time():.2f} milliseconds in {solver.iterations()} iterations')
print()
print(f'Optimal power = {solver.Objective().Value()} 💪power')
print('Army:')
print(f' - 🗡️Swordsmen = {swordsmen.solution_value()}')
print(f' - 🏹Bowmen = {bowmen.solution_value()}')
print(f' - 🐎Horsemen = {horsemen.solution_value()}')
else:
print('The solver could not find an optimal solution.')
================= Solution =================
Solved in 87.00 milliseconds in 2 iterations
Optimal power = 1800.0 💪power
Army:
- 🗡️Swordsmen = 6.0000000000000036
- 🏹Bowmen = 0.0
- 🐎Horsemen = 5.999999999999999
Отлично! Решатель нашел наилучший вариант: общая сила армии равняется 1800 и состоит из 6 мечников и 6 наездников.
Разберем этот результат.
- Солвер решил взять максимальное количество наездников (6, поскольку у нас всего 600 золота, и стоимость каждого равняется 100).
- Оставшиеся ресурсы потрачены на мечников: имеется 1200 еды — 6*140 = 360 еды осталось, вот почему решатель выбрал 6 мечников.
- Вы можете заключить, что наездники — самый лучший юнит, а лучники — худший, потому что они совсем не были выбраны.
Однако в этом результате есть нечто странное: числа некруглые, хотя мы определили, что хотим целочисленные переменные (IntVar). Так что же произошло?
К сожалению, для ответа на данный вопрос нужно глубоко погрузиться в линейное программирование. Чтобы не усложнять, предположим, что причина в GLOP. У решателей имеются характеристики, с которыми нужно считаться, а GLOP не справляется с целочисленными переменными. Вот еще одно доказательство, что создание моделей для многоразового применения — не просто удобство.
Заключение
Мы рассмотрели пять основных шагов любой задачи линейной оптимизации на примере.
- Выбор решателя. В данном случае был выбран GLOP.
- Указание переменных. Параметрами для оптимизации были количество мечников, лучников и наездников.
- Указание ограничений. Каждый юнит имеет цену. Общая цена не может превышать ограниченные ресурсы.
- Указание цели. Критерием для максимизации была общая сила армии. Здесь могло быть и что-то другое, например количество юнитов.
- Оптимизация. GLOP нашел оптимальное решение этой задачи менее, чем за секунду.
Основное преимущество линейного программирования — алгоритм дает гарантию, что найденное решение оптимально (с определенной погрешностью). Это надежная гарантия, но у нее есть цена: модель может быть такой сложной, что солверу потребуются годы (или больше) для нахождения наилучшего решения. В таком случае есть два варианта.
- Остановить решатель через определенное время (и, вероятно, получить субоптимальный ответ).
- Использовать метаэвристику, например генетический алгоритм, чтобы вычислить идеальное решение за короткий промежуток времени.
Читайте также:
- Что нужно знать разработчику ПО
- Работа с панелью индикаторов. Руководство программиста Python. Часть 3
- Обзор инструментов для автоформатирования кода Python
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Maxime Labonne: Introduction to Linear Programming in Python






