Замечали ли вы, что одни программы выполняются дольше, чем другие? Причиной задержки может быть, например, используемый компьютер. Но предположим, что у вас хороший компьютер с мощным процессором. Тогда в чем причина?
Дело в том, что время выполнения написанной программы зависит от переданных входных данных.
Но как выяснить, эффективна ли программа? Есть ли способ это определить? Как проверить, при передаче каких входных данных программа работает лучше всего?
Прежде чем перейти к ответам, разберемся с тем, как вообще работает эффективная программа. И в этом поможет одна забавная история.
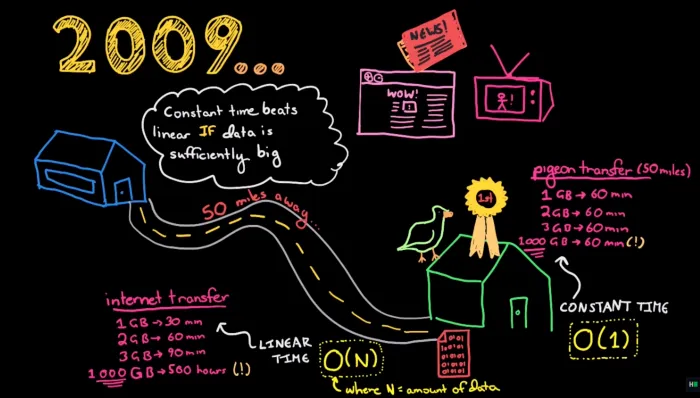
Однажды в компании, которой надоел медленный интернет, было решено провести ряд тестирований. Передачу данных из одного места в другое, находящееся на расстоянии 50 км, проводили одновременно двумя методами.
Один метод заключался в использовании почтового голубя, к лапке которого привязали USB-флешку.

Вторым методом было использование интернета в тех же целях, что и голубя.
Самое интересное заключалось в том, что голубь обогнал интернет. Но как?
Если голубю потребовалось время, чтобы добраться до места, независимо от размера данных, то время достижения интернет-сигнала меняется в зависимости от размера данных.
Перейдем к вычислительным сложностям
Вот две сложности, связанные с программированием.
- Временная: время, необходимое для обработки входных данных.
- Пространственная: количество места, требуемое для обработки входных данных.
Что такое нотация “О” большое?
Этот термин используется в программировании для описания вычислительной сложности алгоритма. В частности, он позволяет оценить, сколько времени требуется для запуска программы.
Проще говоря, термином “О” большое определяется, как время выполнения растет по мере увеличения входных данных.
- Увеличение времени выполнения. Поскольку время, необходимое для выполнения программы, зависит от процессора компьютера, используется “О” большое, чтобы показать, как меняется время выполнения.
- Ввод данных. Поскольку проверяется не только время, которое требуется для выполнения программы, но и ввод, в нотации “О” большое есть “n”, которое определяет количество элементов обрабатываемых входных данных. Поскольку время выполнения растет с увеличением размера входных данных, эту величину можно представить в виде O(n).
- По мере увеличения входных данных. По мере увеличения входных данных программам иногда требуется больше времени для выполнения, что приводит к проблемам с производительностью. Поэтому разрабатываемую программу нужно проверять по мере увеличения входных данных.
Визуализированные примеры
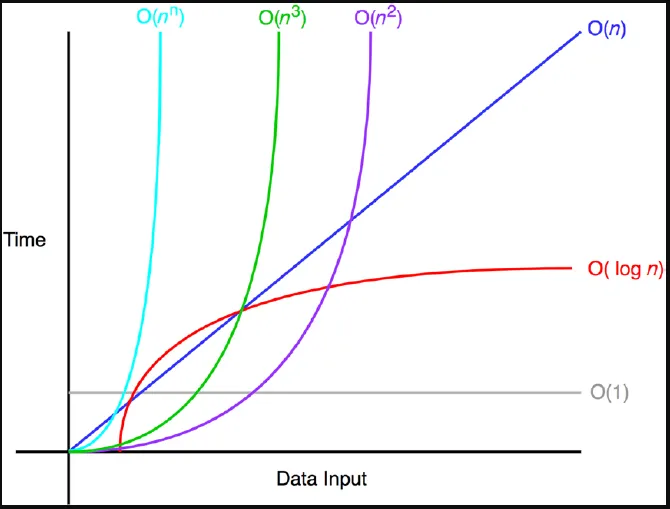
O(1)
O(1) не увеличивается с изменением размера входных данных. Таким образом, время обработки O(1) — величина постоянная независимо от того, какие входные данные были переданы.
Пример:
let names = ['Atit', 'mahesh', 'ramesh', 'kamlesh'];
let data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
function checkLength(data) {
return data.length;
}
console.log(checkLength(names)); // 4
console.log(checkLength(data)); // 10В данном случае, независимо от того, какие входные данные были переданы, сложность останется равной O(1).
Линейная | O(n)
Линейная временная сложность означает, что время пропорционально входным данным. Время будет меняться в зависимости от входных данных.
Пример:
function print(array) {
for (var i = 0; i < array.length; i++) {
console.log(array[i]);
}
}
print(names) //4 times
print(data) //10 timesКвадратичная | O(n²)
Показывает производительность пропорционально размеру входных данных. O(n²) представляет наихудшую производительность.
Пример:
function testdata(data) {
data.forEach(function(items) {
console.log('values ', data);
items.forEach(function(number) {
console.log('Marks', number); //
});
});
}
const test = [
['maths', 52],
['science', 65],
['english', 72]
]
testdata(test)Логарифмическая | O(log n)
Логарифмическая сложность представляет время, необходимое для выполнения алгоритма, пропорциональное логарифму количества элементов (n) входных данных.
Пример:
function log(n) {
for (let i = 1; i < n; i = i * 2) {
const result = i;
console.log(result);
}
}
log(4); //2Для данной программы с любыми итерациями значение i = i*2. Поэтому на n-й итерации значение i= i*n и i всегда меньше размера самого цикла (N).
Следовательно, можно получить:
2^n < N
log(2^n) < log(N)
n < log(N)Таким образом, наихудшая временная сложность такого алгоритма будет равна O(log(n)).
Отбросим константы
Существует вероятность того, что O(N) код быстрее, чем O(1) код для определенных входных данных. “О” большое просто описывает скорость увеличения. По этой причине мы отбрасываем константу, что означает, что O(3N) на самом деле O(N):
- O(3N) → O(N)
Можно отбросить не только константы, но и неглавные члены:
- O(N3+N) → O(N3)
- O(N+logN) → O(N)
- O(2∗2N + 1000N100) → O(2N)
Как вычислить сложность?
Очевидно, что сложность различается в зависимости от структуры кода, используемого в алгоритме. Рассмотрим несколько примеров кода и их сложность.
Циклы (Loops)
- Внутри цикла операторы повторяются n раз. Если для выполнения кода требуется сложность O(m), то внутри n раз повторенного цикла она будет равна n∗O(m) или O(n∗m).
for (let i in arr1) {
print(i);
}- Количество циклов будет равно 4, а выполнение кода внутри цикла равно O(1), поэтому суммарное выполнение будет равно O(4).
Вложенные циклы (Nestedloops)
- Если один цикл находится внутри другого цикла, сложность будет расти экспоненциально. Другими словами, если сложность простого цикла равна O(n), добавление еще одного цикла внутри этого цикла сделает сложность O(n²).
for (let i in arr1) {
print(i);
for (let j in i) {}
}- Здесь сложность первого цикла равна O(5), поскольку количество массивов равно 5, поэтому вложенный цикл также выполняется с той же сложностью 5 раз, а значит, оба цикла будут O(5²).
Читайте также:
- Важные аспекты математики в науке о данных - «что» и «почему»
- Решение алгоритмических проблем: Поиск повторяющихся элементов в массиве
- 8 показателей эффективности классификации
Читайте нас в Telegram, VK и Дзен
Перевод статьи Atit Patel: What is “Big O Notation” in Programming?






