Проблема

  • Найти дубликат в массиве
Given an array of n + 1 integers between 1 and n, find one of the duplicates.

If there are multiple possible answers, return one of the duplicates.
If there is no duplicate, return -1.

Example:

Input: [1, 2, 2, 3]
Output: 2

Input: [3, 4, 1, 4, 1]
Output: 4 or 1

Категория: массивы

Процесс решения задачи

Перед тем как вы увидите решение, давайте немного поговорим о самой проблеме. У нас есть: массив n + 1 элементов с целочисленными переменными в диапазоне от 1 до n.

Например: массив из пяти integers подразумевает, что каждый элемент будет иметь значение от 1 до 4 (включительно). Это автоматически означает, что будет по крайней мере один дубликат.

Единственное исключение — это массив размером 1. Это единственный случай, когда мы получим -1.

Brute Force

Метод Brute Force можно реализовать двумя вложенными циклами:

for i = 0; i < size(a); i++ {
  for j = i+1; j < size(a); j++ {
    if(a[i] == a[j]) return a[i]
  }
}

O(n²) — временная сложность и O(1) — пространственная сложность.

Count Iterations

Другой подход, это иметь структуру данных, в которой можно перечитать количество итераций каждого элемента integer. Такой метод подойдёт как для массивов, так и для хэш-таблиц.

Реализация на Java:

public int repeatedNumber(final List<Integer> list) {
  if(list.size() <= 1) {
    return -1;
  }
  
  int[] count = new int[list.size() - 1];

  for (int i = 0; i < list.size(); i++) {
    int n = list.get(i) - 1;
    count[n]++;

    if (count[n] > 1) {
      return list.get(i);
    }
  }

  return -1;
}

Значение индекса i представляет число итераций i+1.

Временная сложность этого решения — O(n), но и пространственная — O(n), так как нам требуется дополнительная структура.

Sorted Array

Если мы применяем метод упрощения, то можно попытаться найти решение с отсортированным массивом.

В этом случае, нам нужно сравнить каждый элемент с его соседом справа.

Реализация на Java:

public int repeatedNumber(final List<Integer> list) {
  if (list.size() <= 1) {
    return -1;
  }

  Collections.sort(list);

  for (int i = 0; i < list.size() - 1; i++) {
    if (list.get(i) == list.get(i + 1)) {
      return list.get(i);
    }
  }

  return -1;
}

Пространственная сложность O(1), но временная O(n log(n)), так как нам нужно отсортировать коллекцию.

Sum of the Elements

Ещё один способ — это суммирование элементов массива и их сравнение с помощью 1 + 2 + … + n.

Рассмотрим пример:

Input: [1, 4, 3, 3, 2, 5]
Sum = 18

As in this example, we have n = 5:
Sum of 1 to 5 = 1 + 2 + 3 + 4 + 5 = 15

=> 18 - 15 = 3 so 3 is the duplicate

В этом примере мы можем добиться результата временной сложности O(n) и пространственной O(1). Тем не менее, это решение работает только в случае, когда мы имеем один дубликат.

Нерабочий пример:

Input: [1, 2, 3, 2, 3, 4]
Sum = 15

As in this example we have n = 5,
Sum of 1 to 5 = 1 + 2 + 3 + 4 + 5 = 15

/!\ Not working

Такой способ приведёт в тупик. Но иногда, чтобы найти оптимальное решение, нужно перепробовать всё.

Marker

Кое-что интересное стоит упомянуть. Мы рассматривали решения, не учитывая условия, что диапазон значений integer может быть от 1 до n. Из-за этого примечательного условия каждое значение имеет свой собственный, соответствующий ему индекс в массиве.

Суть этого решения в том, чтобы рассматривать данный массив как список связей. То есть значение индекса указывает на его содержание.

Пример с [2, 3, 3, 1]

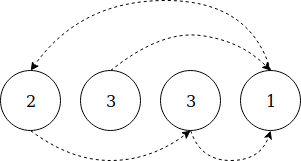
Мы проходим через каждый элемент и помечаем соответствующий индекс, прибавляя к нему знак минус. Элемент является дубликатом, если его индекс уже помечен минусом.

Давайте рассмотрим конкретный пример, шаг за шагом:

Input: [2, 3, 3, 1]

* Iteration 0:
    Absolute value = 2
    Put a minus sign to a[2] => [2, 3, -3, 1]

* Iteration 1:
    Absolute value = 3
    Put a minus sign to a[3] => [2, 3, -3, -1]

* Iteration 2:
    Absolute value = 3
    As a[3] is already negative, it means 3 is a duplicate

Реализация на Java:

public int repeatedNumber(final List<Integer> list) {
  if (list.size() <= 1) {
    return -1;
  }

  for (int i = 0; i < list.size(); i++) {
    if (list.get(Math.abs(list.get(i))) > 0) {
      list.set(Math.abs(list.get(i)), -1 * list.get(Math.abs(list.get(i))));
    } else {
      return Math.abs(list.get(i));
    }
  }

  return 0;
}

Это решение даёт результат временной сложности O(n) и пространственной O(1). Тем не менее, потребуется изменять список ввода.

Runner Technique

Есть ещё один способ, который предполагает рассматривать массив как некий список связей (повторюсь, это возможно благодаря ограничению диапазона значений элементов).

Давайте проанализируем пример [1, 2, 3, 4, 2]:

Пример с [1, 2, 3, 4, 2]

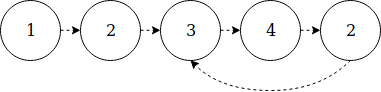
Такое представление даёт нам понять, что дубликат существует, когда есть цикл. Более того, дубликат проявляется на точке входа цикла (в этом случае, второй элемент).

Мы можем взять за основу алгоритм нахождения цикла по Флойду, тогда мы придём к следующему алгоритму:

  • Инициировать два указателя slow и fast
  • С каждым шагом: slow смещается на шаг со значением slow = a[slow], fast смещается на два шага со значением fast = a[a[fast]]
  • Когда slow == fast ― мы в цикле.

Можно ли считать этот алгоритм завершённым? Пока нет. Точка входа этого цикла будет обозначать дубликат. Нам нужно сбросить slow и двигать указатели шаг за шагом, пока они снова не станут равны.

Возможная реализация на Java:

public int repeatedNumber(final List<Integer> list) {
  if (list.size() <= 1)
    return -1;

  int slow = list.get(0);
  int fast = list.get(list.get(0));

  while (fast != slow) {
    slow = list.get(slow);
    fast = list.get(list.get(fast));
  }

  slow = 0;
  while (fast != slow) {
    slow = list.get(slow);
    fast = list.get(fast);
  }
  return slow;
}

Это решение даёт результат временной сложности O(n) и пространственной O(1) и не требует изменения входящего списка.

Перевод статьи Teiva Harsanyi : Solving Algorithmic Problems: Find a Duplicate in an Array

 

Предыдущая статьяJava для начинающих. Часть 1 из 4
Следующая статьяJava для начинающих: часть 2 из 4