Что такое графы?
Спросите специалиста из любой области науки, как работает предмет его исследований. Наверняка он предложит вам рассмотреть некую систему с существующими внутри нее связями. Это может быть человеческое тело, пищевая цепочка в экосистеме, химическая реакция или общество в целом. Не понимая взаимоотношений между парой животных в экосистеме, двумя атомами в молекуле или клетками и тканями в нашем организме, вы просто получите кучу данных: перечень клеток, выборку информации о питании животных и т. д.
Традиционные модели машинного обучения зачастую извлекают данные следующим образом: берут информационные единицы из списков или таблиц и обрабатывают их (детали этого процесса зависят от используемого алгоритма, а также от нескольких других параметров). Так делаются различные прогнозы. Однако некоторые проблемы решаются более эффективным способом.
Графы — это структуры данных, которые представляют собой сети с парными связями внутри. Как правило, они представлены в виде “узлов” и линий, или “ребер”.

На рис.1 приведен пример “неориентированного графа”, в котором данные имеют двунаправленную связь с другими данными. Каждый узел этого графа представляет пользователя социальной сети, все участники которой связаны друг с другом. В таком виде можно изобразить сетевой сайт, например LinkedIn, где, связываетесь с кем-то, вы сразу оказываетесь связаны с остальными пользователями. Примером ориентированного (направленного) графа может быть Twitter — социальная сеть, пользователи которой следуют друг за другом (и не всегда взаимно).
Изображения, представляющие данные (пользователей), называются узлами или вершинами, а линии, соединяющие их, — ребрами. Интенсивность связи между вершинами передают линии:
- пунктирные означают более слабые отношения типа “все или ничего” (т. е. вы следуете за кем-то или нет);
- сплошные выражают “взвешенные” отношения (т. е. представляют более высокий уровень вовлеченности в отношения между двумя пользователями).
Вероятно, в данный момент вы чувствуете то же, что и я, когда меня впервые познакомили с графами и теорией графов на уроке информатики: скучно и не совсем ясно. Но у меня есть для вас хорошая новость: после знакомства с базовыми терминами, необходимые для понимания предмета обсуждения, мы приступаем к более интересным вопросам: почему графы важны и что делает их столь крутыми.
Итак, с чем мы имеем дело?
Графы уже применяются в информатике для создания некоторых довольно крутых приложений. Maps, например, использует графы для хранения данных о локациях и улицах, которые их соединяют. В этом же приложении нашли применение алгоритмы кратчайшего расстояния, призванные находить самый короткий маршрут к месту назначения.
Но это цветочки, ягодки будут, когда мы начнем рассматривать использование графов в машинном обучении. Поскольку графы демонстрируют всесторонние связи между фрагментами данных (по сравнению с упорядоченными списками данных или тензорами, которые сами по себе мало говорят нам о связях между величинами или объектами), мы можем использовать их для проведения комплексного анализа и на его основе делать прогнозы.
Теория графов & машинное обучение — но как?
Прежде чем воспользоваться преимуществами тандема графов с машинным обучением, мы должны представить наши связи так, чтобы компьютер — а затем алгоритм машинного обучения — смог их понять.
Графы обычно могут быть представлены одним из трех основных способов.
1. Матрица примыканий
Суть матрицы примыканий раскрывается в самом ее названии: соединения, или ребра, между различными узлами представлены с использованием матричных ячеек. Чтобы проиллюстрировать, как это может выглядеть, приведем следующий пример:
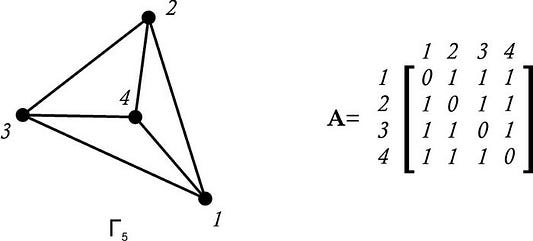
Эта матрица поможет найти ребро между двумя узлами по пересечению меток в матрице. Мы можем видеть, например, что узел 1 не связан сам с собой, но связан с узлом 2.
2. Список ребер
Список ребер — это способ представить нашу сеть, или граф, в вычислительном отношении. Для этого в списке указываются пары связанных узлов. Вы можете видеть это на примере ниже:
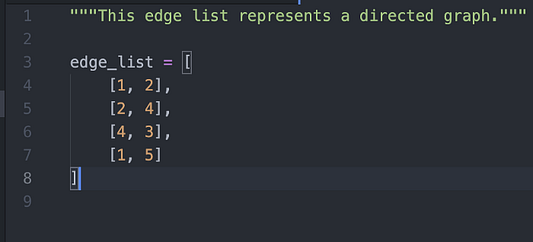
3. Список примыканий
Списки примыканий объединяют в себе два вышеперечисленных подхода, представляя список узлов, связанный со списком всех узлов, к которым они напрямую примыкают. Чтобы проиллюстрировать это, давайте рассмотрим пример:
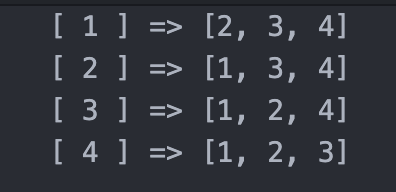
С помощью вышеперечисленных трех подходов мы можем справиться с трудностями представления графов вычислительно в нашем коде. Однако все еще существуют некоторые проблемы при подаче графиков в модели машинного обучения. Традиционно модели глубокого обучения хорошо справляются с обработкой данных, которые занимают фиксированный объем пространства и являются однонаправленными. Графы, независимо от того, как мы их представляем, не занимают фиксированного объема пространства в памяти и не являются непрерывными, а скорее каждый узел содержит ссылку на узлы, к которым он непосредственно примыкает.
Теория графов и машинное обучение — что мы можем с этим сделать?
Ничего не существует в отрыве от всего остального. Понимание взаимосвязанных сетей данных, входящих в состав большинства научных дисциплин, позволит нам найти ответы на множество вопросов. Вот лишь некоторые из них:
- Как лучше исследовать человеческий мозг?
- Как спрогнозировать влияние какого-либо стимула или изменения на экосистему?
- Как понять, какое соединение с наибольшей вероятностью создаст эффективный препарат?
А теперь самое интересное — информация о том, что мы можем. И это не теоретическая возможность, а то, что мы делаем прямо сейчас!
Сферы применения теория графов:
- Диагностическое моделирование (прогнозирование с определенной степенью уверенности, имеет ли пациент конкретный диагноз или нет).
- Помощь в диагностике и лечении онкобольных.
- Разработка фармацевтических препаратов (медикаментов).
- Поиски путей объединения теорий экологии и эволюции.
Как работает теория графов
Давайте немного углубимся в сферы применения теории графов. Возьмем в качестве примера диагностические модели. В частности, я предлагаю рассмотреть пример сетевого анализа мозга, применяемого для выявления реальной или потенциальной шизофрении у пациентов.
Используя графы, нейробиологи могут сопоставить ключевые результаты, связанные с диагнозом шизофрении. При этом учитываются определенные маркеры начала расстройства:
- менее эффективные проводные сети;
- меньше локальной кластеризации;
- менее иерархическая организация.
Основываясь на этих маркерах, мы потенциально могли бы оценить эти сети с помощью алгоритма машинного обучения и предсказать вероятность того, что у пациента есть или будет развиваться шизофрения.
Без понимания этих сетей данный вид диагностики становится совершенно другим неврологическим анализом. Многообещающие открытия в области исследования данных о шизофрении имеют многообещающие последствия для выявления и лечения этого расстройства — возможности ранней диагностики и вмешательства, которые выходят далеко за рамки простой оценки симптомов.
Это всего лишь один пример, но он полностью иллюстрирует преимущества теории графов в машинном обучении, поскольку она пересекается с другими дисциплинами.
Дело в том, что в наших данных часто содержится гораздо больше информации, чем мы можем представить в виде списков, фреймов данных или тензоров. Да, у нас есть способы изучения данных и представления их таким образом, чтобы мы могли выдвигать гипотезы о взаимосвязях и даже позволять нашим алгоритмам предсказывать их. Но когда мы научимся иначе устанавливать связи между нашими данными, мы достигнем куда большего.
Осознавая, как вещи соотносятся друг с другом, мы лучше их понимаем. Мы можем делать более исчерпывающие прогнозы и отвечать на более сложные вопросы с довольно важными результатами, способными изменить нашу жизнь.
Читайте также:
- Продвинутый взгляд на рекурсию
- Графы: основы теории, алгоритмы поиска
- Графы и пути: Алгоритм Брона-Кербоша, максимальные группы
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Sid Arcidiacono, Why Graph Theory Is Cooler than You Thought






