Измерение — это процесс присвоения чисел количествам (переменным). Этот процесс настолько знаком, что мы, наверняка, часто упускаем из виду его фундаментальные характеристики. Единая мера некоего атрибута (к примеру, веса) взятого образца называется статистикой. Эти атрибуты также имеют наследуемые свойства, схожие с числами, которые мы им присваиваем в процессе измерения. Присваивая числа атрибутам, мы можем допускать неточности, тогда свойства чисел не будут соответствовать свойствам атрибутов. В такой ситуации мы получаем “низкий уровень измерения” (другими словами, низкую точность). Точность же относится к абсолютной разнице между измеренным и реальным значениями. И наоборот, если свойства присвоенных чисел должным образом соответствуют свойствам присвоенных атрибутов, то мы получаем высокий уровень измерения (т.е. высокую точность).
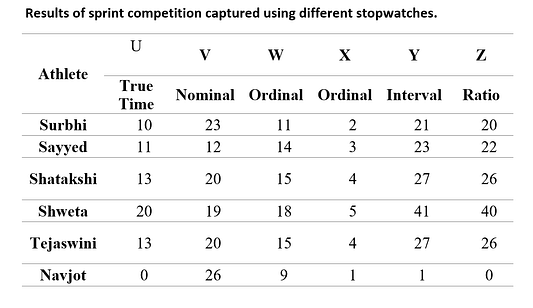
Введение различных уровней измерения приписывают американскому статистику Стенли Смиту Стивенсу. В 1946 году он сказал: “Все измерения в науке проводятся при помощи четырёх разных типов шкал: номинальной, порядковой, интервальной и коэффициента.” Эти уровни расположены в порядке возрастания согласно повышению точности. Это значит, что номинальный уровень имеет самый низкий уровень точности, а коэффициент высочайший. Для дальнейшего рассуждения будет использован пример, в котором шесть спортсменов проходят отбор на позицию спринтера в гонке. Все они бегут 100-метровый отрезок, а результат измеряется несколькими тренерами, использующими разные секундомеры (от U до Z). Истинное время измеряет только секундомер U, остальные же (от V до Z) показывают ошибочный результат, но на других уровнях измерения. Результаты, полученные после стометровки, приведены в таблице ниже.
Номинальный уровень
Номинальная шкала отражает только эквивалентность (одинаковый показатель или другой) и принадлежность множеству. Эти множества принято называть категориями или метками. Перейдём к рассмотрению результатов забега, приведённых в таблице. Секундомер V практически бесполезен, но он отразил базовое свойство показателей времени забега. А именно то, что два отражённых секундомерами значения будут одинаковыми только, если два фактических времени совпадут. Например, участники Shatakshi и Tejaswini пробежали забег за одно время (13с), и, согласно показаниям секундомера V, это базовое свойство остаётся одинаковым (пр 20с). Глядя на результаты секундомера V, можно обоснованно заключить, что Shakatashi и Tejaswini пробежали забег за одинаковое время. Этот атрибут называется эквивалентностью. Мы можем сделать вывод, что секундомер V достиг лишь номинального уровня измерения. Переменные, оцениваемые по номинальной шкале, называются категориальными. К примерам этого относятся имена, пол, раса, религия, национальность, таксономические разряды, части речи, просроченные и непросроченные товары, здоровый или больной, типы геологических пород и пр. Коррелировать две номинальные категории очень сложно, поскольку любые проявляющиеся связи обычно считаются ложными и, следовательно, не имеющими значения. Например, попытка выяснить имена скольких людей из Ассама начинаются с буквы ‘A’ оказалась бы чисто произвольной задачей со случайным результатом.
Порядковый уровень
Порядковая шкала в дополнение ко всем атрибутам, отражённым номинальным уровнем, отражает атрибут рангового порядка. Снова вернёмся к результатам соревнования. Возрастающий порядок времени, затраченного участниками согласно показателям истинного времени (соответствующий ранг указан в скобках), будет следующим: Navjot (1), Surbhi (2), Sayyed (3), Shatakshi/Tejaswini (4) и Shweta (5). Кроме отражения свойства совпадения/отличия номинального уровня, секундомеры W и X отразили верный порядок итогов забега. Мы говорим, что секундомеры W и X достигли порядкового уровня измерения. Примеры измерений на этом уровне включают баллы IQ, академические баллы (оценки), процентили и т.д. Ранговое упорядочение (порядковое измерение) возможно производить при помощи субъективных измерительных опросов. К примеру, опрос общественности в Индии для измерения её согласия с утверждением, что “Люди произошли от животных.” включал выбор участниками подходящего ответа из вариантов: ‘полностью согласен’, ‘скорее согласен’, ‘скорее несогласен’, ‘совершенно несогласен’.
Интервальный уровень
Шкала интервалов в дополнение ко всем атрибутам номинального и порядкового уровней отражает атрибут относительного расстояния. Другими словами, измерения на интервальном уровне находятся в правильной пропорции. Снова рассмотрим результаты соревнования. Значения в колонке Y (показания секундомера Y) при помощи простой формулы, являющейся линейным уравнением, могут быть получены из значений в колонке U (показания секундомера U):
Y=2U+1
Например, первые показания, 21 (время забега Surbhi) могут быть получены подстановкой в формулу выше: Y=(2x 10)+1=21.
Отличительной чертой шкалы интервалов является ‘относительное расстояние’ или пропорция. Коэффициенты разности значений на интервальном уровне остаются такими же, как и у истинного времени. Например, рассмотрим значения в колонке Y (Shatakshi-Surbhi)/(Sayyed-Surbhi)
= (27–21)/(23–21)
= 6/2
= 3
Давайте выполним ту же операцию для значений из колонки U:
= (13–10)/(11–10)
= 3/1
= 3
Обратите внимание, что относительное расстояние, 3, остаётся одинаковым между измерением на интервальном уровне и измерением реального времени. Другими словами, глядя на секундомер Y, можно с уверенностью заключить, что разница во времени (Shatakshi-Surbhi) в три раза (относительное расстояние 3) больше разницы времени (Sayyed-Surbhi). При измерении интервалов разница между двумя значениями играет важную роль. Тем не менее стоит отметить, что абсолютное расстояние различно, и совпадает лишь относительное. Когда числа отражают совпадение/различие, имеют правильный порядок и правильное относительное интервальное расстояние, мы говорим, что они достигли интервального уровня измерения.
Один из примеров измерения на уровне интервалов — это шкала Цельсия. Единицы измерения в Цельсиях (т.е. 1 °C) определяются как “1/100 разницы температур между точками замерзания и закипания воды при давлении в 1 атмосферу”. Обратите внимание, что определение основано на принципе относительного расстояния, описанном выше. Поскольку уровень интервальный, абсолютное расстояние окажется неподходящим. Тем не менее будет правильным заключить, что: “разница между температурой 50 °C и 40 °C такая же, как между 20 °C и 10 °C.”
Кроме того, стоит заметить, что показания ‘0’ не соответствуют отсутствию измеряемого на этом уровне атрибута. Например, 0 °C не означает отсутствие температуры. Другие примеры измерений, попадающих в интервальную шкалу, включают температуру по шкале Фаренгейта, проценты, даты, измеряемые от произвольной эпохи (например от Рождества Христова), положение по декартовым координатам, географическое положение по широте и долготе, высоту над уровнем моря, направление, измеряемое в градусах от истинного или магнитного юга и т.д.
Уровень коэффициента
Шкала коэффициента в дополнение ко всем атрибутам, отражённым номинальным, порядковым и интервальным уровнями, отражает атрибут коэффициента. И снова вернёмся к результатам в таблице. Значения в колонке Z (показания секундомера Z) могут быть получены из показаний колонки U (секундомер U — истинное время) с помощью простой формулы:
Z=2U
Коэффициент измерений между Z и U остаётся одинаковым. Например, коэффициент соотношения (Sayyed/Shatakshi) в колонке Z (22/26) такой же, как и в колонке U (11/13). Глядя на колонку Z, можно уверенно заключить, что “Shweta бежал вдвое дольше, чем Surbhi”. Также обратите внимание, что точка отсчёта секундомера верна. Navjot не участвовал в забеге, поэтому в показаниях секундомеров U и Z мы видим 0. Отсюда следует, что шкала коэффициента имеет ‘абсолютный ноль’ (точку, где измеряемых качеств не существует). Например, ‘ноль градусов’ на шкале Кельвина (находящейся на уровне коэффициента) означает полное отсутствие температуры.
Большая часть научных и инженерных измерений выполняется на шкалах коэффициента. В науке измерение обычно определяется как вычисление коэффициента между значением непрерывной величины и величиной единицы измерения того же рода. Некоторые примеры измерений по шкале коэффициента: концентрация химического вещества, плотность потока фотосинтетических фотонов, температура в Кельвинах, масса, длина, время, угол на плоскости, энергия, давление и электрический заряд.
Определить по какой шкале производится измерение: интервальной или коэффициента можно, задав два вопроса: имеет ли здесь смысл ноль? Допустимы ли операторы удвоения или деления пополам?
Также важно отметить, что некоторые научные измерения не попадают ни в один из этих уровней. Их примеры включают шкалу pH и значения logIC50. Оба этих измерения проводятся по логарифмической шкале. Как бы то ни было, когда эти значения выражаются на шкале концентрации (H+ion концентрация для значений pH или IC50), измерения попадают в уровень коэффициента.
Выводы
- Измерение — это процесс присваивания чисел количествам (переменным).
- Большинство измерений в науке выполняются с использованием четырёх типов шкал: номинальной, порядковой, интервальной и коэффициента.
- Номинальный уровень отражает атрибуты эквивалентности и принадлежности множеству. Например, мой доход совпадает с вашим или отличается.
- Порядковый уровень отражает атрибут рангового порядка. Например, если наши доходы различны, мой больше или меньше вашего.
- Интервальный уровень отражает относительную разницу атрибута. Например, разница между моим доходом и вашим может быть, скажем, вдвое больше, чем разница между моим доходом и доходом профессора.
- Шкала коэффициента отражает атрибуты коэффициента и точки отсчёта. Например, доход моего брата примерно в 10 раз больше, чем у меня.
Читайте также:
- Внедрение зависимостей, или Разработчики совсем обленились
- 6 технологий, которые помогут стать востребованным фронтенд-разработчиком в 2021
- Программирование- это искусство и никак иначе!
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Riteshpratap A. Singh: Levels of Measurements.