
Поскольку Rust приобрел довольно широкую известность и пополнил ряды своих преданных поклонников, я решил отложить в сторону любимый JS и заняться изучением нового языка. Должен сказать, что предприятие не для слабонервных. К счастью, за исключением редких случаев недопонимания, компилятор — ваш верный друг, поскольку всегда укажет на ошибки и даже предложит решения. Посвятив освоению языка какое-то время и преодолев первый крутой подъем кривой обучаемости, вы начинаете влюбляться в Rust — что со мной и произошло!
В этой статье во всей красе Rust будет представлена реализация моей любимой структуры данных: двоичного дерева. Это обычное дерево, которое состоит из узлов, содержащих (потенциально глубоко) вложенные значения. Особенностью такого дерева является наличие у его узлов только двух дочерних значений: левого и правого. Как правило, подобные структуры служат для представления математических выражений, но могли бы использоваться и для парсинга простых грамматик. В интересах планируемой реализации нашим узлам также полезно было бы узнать, какой тип операции они представляют. Постараемся придать ей обобщенный вид без привязки базовой структуры к какому-либо типу. Перед вами простое представление двоичного дерева:
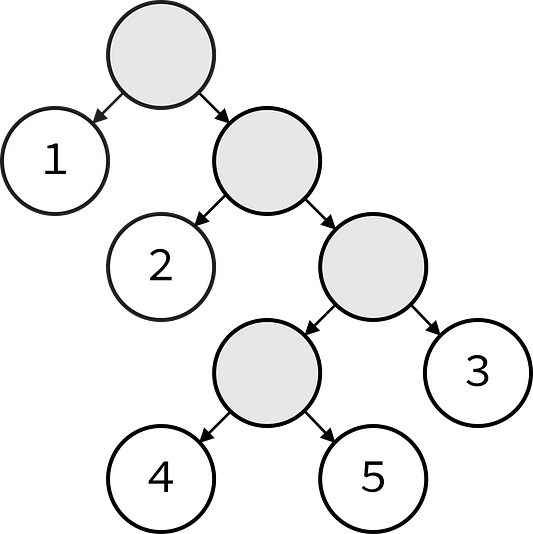
На этом изображении терминальные узлы отмечены цифрами. Обратите внимание, что двоичные деревья смещены влево и расположены в глубину. Это значит, что при обходе дерева процесс вычисления начнется с самого дальнего левого узла, рекурсивно переходя от узлов левее к узлам правее. Далее я объясню более подробно.
Придумаем минимальную структуру для представления данных узла:
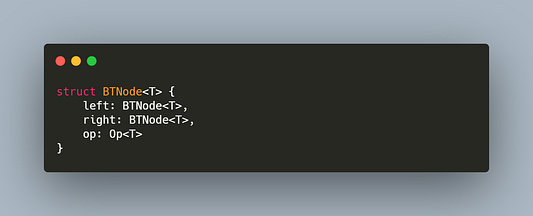
…компилятор тут же на нас разозлился. Структура не может напрямую ссылаться на саму себя, поскольку она становится рекурсивным типом, что недопустимо в Rust. Но, к счастью, есть возможность поместить рекурсивные узлы в Box, тем самым косвенно показав, что это указатель, ссылающийся на объект в куче. Посмотрим, поможет ли данный прием решить нашу проблему:
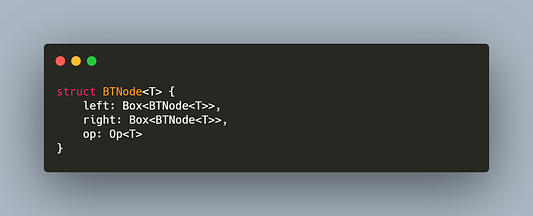
Сработало. Box добавил уровень косвенной адресации через сохранение указателя на BTNode, позволяя нам обойти запрет на рекурсивный тип. А что же насчет Op? Им будет enum, представляющее возможные операции с узлами. В нашем примере ограничимся простыми арифметическими действиями:

Довольно просто. У нас есть вариант для нескольких базовых арифметических операций. Обратили внимание на Id(T)? Это особая операция. Поскольку нам необходимо, чтобы значения в дереве были экземплярами структур BTNode, нет никакой возможности поместить в него i32 напрямую. Проблема в том, что согласно нашим ожиданиям терминальными значениями должны быть исходные числа. Допустим, у нас есть выражение (3 + 4) * (5 * 2). Можно представить его в виде дерева с тремя узлами: корневой узел Mul с левым и правым значениями узлов; его левый потомок — узел Add с левым и правым значениями, т. е. 3 и 4; и правый потомок — узел Mul со значениями 5 и 2. Эти исходные числа называются терминальными значениями.
Такое название обусловлено тем, что эти узлы располагаются на концах дерева. Если обычный узел — это ветвь, то терминальный — это лист. Достигнув подобного узла, вы не увидите более глубоких вложений, по которым можно было бы пройти вслед за выполнением кода, в связи с чем его внутреннее значение можно истолковать как исходное значение, а не как узел. Чтобы получить терминальные значения из узлов, необходимо выбрать для сохранения данных вариант Op::Id(T) . Пока мы на этом этапе, вероятно, стоит подумать о том, что упакованные в Box левый и правый узлы могут быть не определены в терминальном узле. С учетом этого каждый из них следует обернуть в Option:
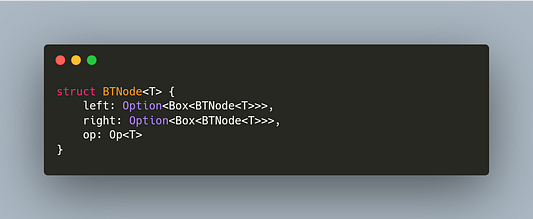
Итак, мы определили узлы таким образом, чтобы их потомки могли быть упакованным значением Some или None. Хотя, определенно, это выглядит презабавно. Придадим коду чуть более привлекательный вид с помощью псевдонима типа:

Можно разместить эту инструкцию в начале кода, заменив длинную версию в BTNode. Досконально продумав способ определения узлов, перейдем к определению дерева:
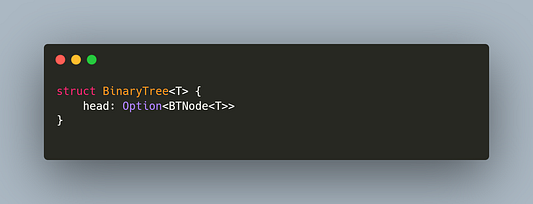
Поскольку мы уделили достаточно времени определению узлов, дальше сложностей уже не возникнет. Наше дерево либо пустое, либо его вершина содержит значение Some. Поскольку вложенные узлы являются значениями указателей на узлы-потомки, то у нас есть все необходимое для определения дерева. Поработав с его данными, приступим к реализации и начнем с узлов.
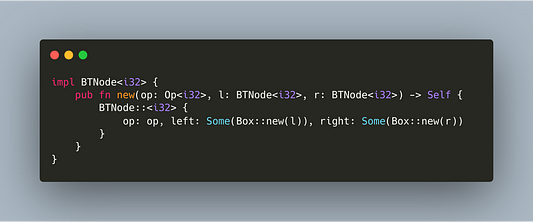
Ничего сложного. Конструктор был вертикально расширен, и теперь у нас есть способ создавать экземпляры структуры узлов. А представьте процесс объявления new для каждого узла — написать придется немало! Предлагаю внести немного абстракции и создать специальные конструкторы.
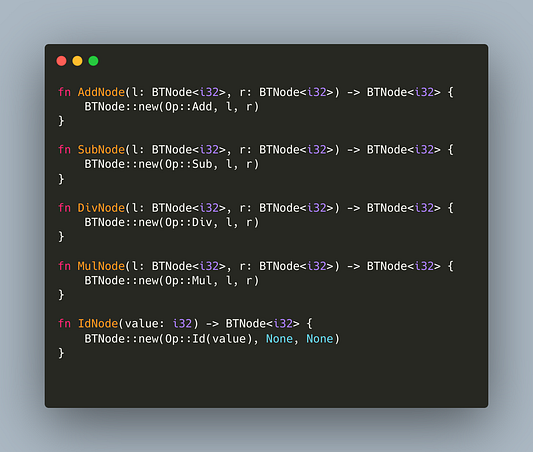
Каждая из этих функций создает специальную версию BTNode, которая в дальнейшем упрощает их объявление. Все они отталкиваются от исходного конструктора BTNode::new, за исключением IdNode, создающей BTNode напрямую, поскольку значения его правого и левого узлов не важны, и ее интересует только значение i32.
Настало время подумать о реализации какой-нибудь функциональности для дерева. Ему нужна одна главная функция — обход узлов для получения одного значения. Нам предстоит ее написать.
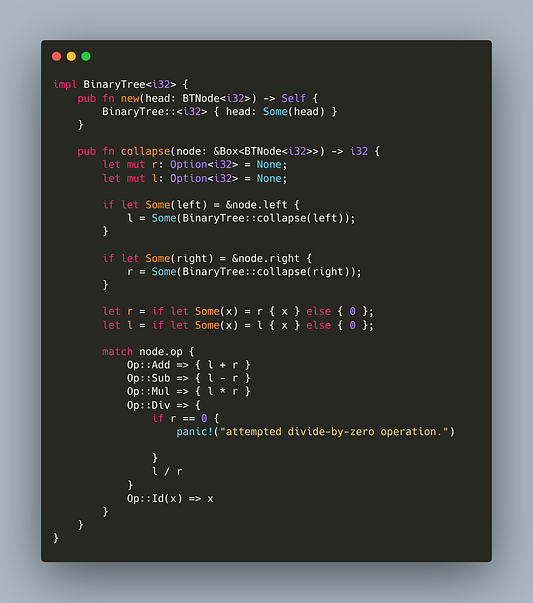
Я также включил простой конструктор. Давайте разберем этот код. Если посмотреть на сигнатуру для реализации i32, то увидим, что она принимает ссылку указателя на узел и возвращает i32. Прежде всего мы объявляем изменяемую пару левого и правого значений Option<i32> и инициализируем их как None — после обхода узлов-потомков сможем их переприсвоить . Далее рекурсивно вызываем collapse для узлов-потомков, чтобы переприсвоить левое и правое значения только при условии, что любое из них является нетерминальным узлом, т. е. узлом, не принадлежащим к IdNodes. Затем наступает очередь if let с левым и правым значениями для извлечения их в i32. Во время этой операции мы переопределяем переменные l и r как неизменяемые (когда повторно объявляем их с помощью let). Наконец, мы сопоставляем операцию узлов, объединяя и возвращая значения (или вызываем panic! при случайном делении на 0).
Создадим дерево на основе этого рисунка:
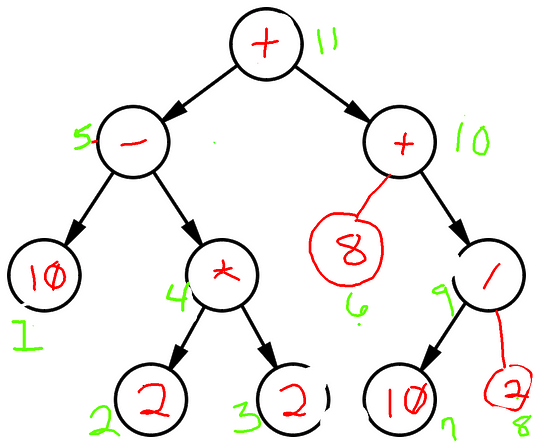
Это дерево представляет выражение (10 - (2 * 2)) + (8 + (10 / 2)). Зеленые числа указывают порядок, согласно которому алгоритм обходит узлы, а красные будут использоваться в качестве значений узлов.
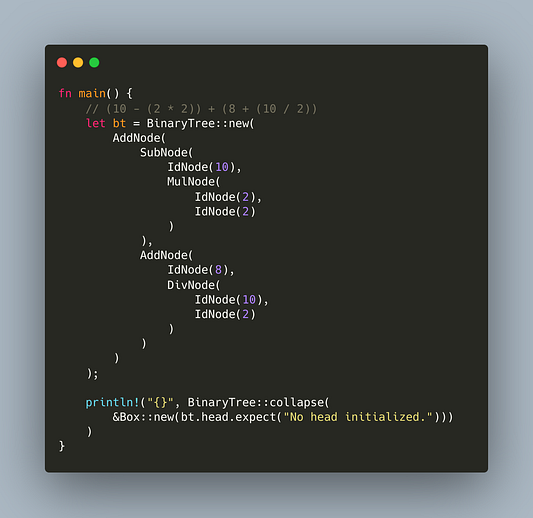
В консоли должен появиться вывод 19. Такой же результат получился бы и у нас, если бы сами выполнили обход по узлам.
По этой ссылке можно перейти в “песочницу” Rust и поэкспериментировать с кодом.
В статье был рассмотрен простой пример, но Op enum вполне способен представлять и что-нибудь другое. Мы могли бы реализовать дерево для другого типа, применив его в иных целях, например для парсинга простой грамматики скрипта или накопления специальных эффектов в видео игре. В мире компьютерной науки такая структура данных, как двоичное дерево, находит себе успешное практическое использование.
Благодарю за внимание и надеюсь, что материал статьи был для вас полезен.
Читайте также:
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Ross: Rust: Binary Tree






