Алгоритм Рабина-Карпа с полиномиальным хешем и модульной арифметикой

Введение

Созданный Ричардом Карпом и Майклом Рабином алгоритм Рабина-Карпа  —  это алгоритм поиска строки, который использует хеширование для поиска совпадений между заданным шаблоном поиска и текстом.

Наивный алгоритм поиска строки сравнивает заданный шаблон со всеми позициями в тексте. Это приводит к далеко не идеальной сложности времени исполнения O(nm), где n = длина текста, а m = длина шаблона.

Алгоритм Рабина-Карпа совершенствует этот подход за счёт того, что сравнение хешей двух строк выполняется за линейное время: для поиска совпадения это гораздо эффективнее, чем сравнение отдельных символов этих строк. Таким образом, алгоритм показывает лучшее время исполнения O(n+m).

Алгоритм Рабина-Карпа

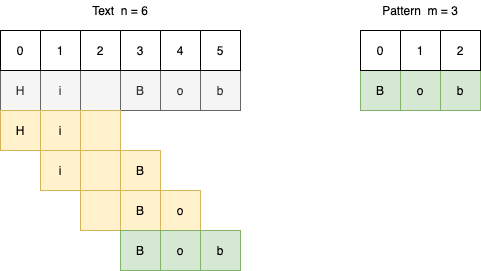
1. Вычисляется хеш шаблона строки.
2. Вычисляется хеш подстроки в тексте строки, начиная с индекса 0 и до m-1.
3. Сравнивается хеш подстроки текста с хешем шаблона.

• Если они совпадают, то сравниваются отдельные символы для выявления точного совпадения двух строк.
• Если они не совпадают, то окно подстроки сдвигается путём увеличения индекса и повторяется третий пункт для вычисления хеша следующих m символов, пока не будут пройдены все n символов.

Хеш-функция

С применением хеш-функции связаны два нюанса.

Во-первых, алгоритм хорош настолько, насколько хороша его хеш-функция. Если при использовании хеш-функции имеют место многочисленные ложные срабатывания, то сравнение символов будет выполняться слишком часто. В этом случае очень сложно считать этот метод более эффективным, чем наивный алгоритм.

Во-вторых, каждый раз, когда подстрока проходит по тексту, вычисляется новый хеш, что крайне неэффективно, ведь в этом случае производительность такая же, если не хуже, как у наивного алгоритма.

Обе эти проблемы решаются с помощью полиномиального хеша с операциями сложения и умножения. И хотя это не какой-то эксклюзив алгоритма Рабина-Карпа, которого нет в других алгоритмах, здесь он работает так же хорошо.

Полиномиальный кольцевой хеш

Вот как выглядит вычисление полиномиального хеша, построенного на операциях сложения у умножения:

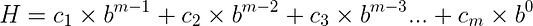
Пример

Не будем заниматься преобразованием символов, а сразу используем целые числа.

Дан шаблон 135 и текст 2135 с основанием b = 10.

Сначала вычисляем хеш шаблона 135:

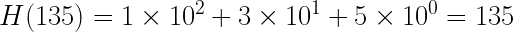
Затем вычисляем хеш первых m = 3 символов текста, т. е. 213:

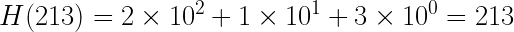
Совпадения не произошло. Теперь сдвигаем подстроку, отбросив первый символ предыдущего окна и добавив следующий. Получилось новая 135. Вычисляем для неё хеш:

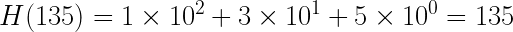
Хеши совпадают, и алгоритм фактически подходит к своему завершению.

Скользящий хеш

Обратите внимание: переместив сдвигающее, а лучше сказать, скользящую подстроку, нам пришлось вычислить весь хеш 213 и 135. А это нежелательно, так как при этом мы вычислили хеш целых чисел, которые уже были в предыдущем окне.

Скользящая хеш-функция может запросто устранить эти дополнительные вычисления, убрав из подсчёта хеша нового окна первый символ предыдущего и добавив новый символ.

Теоретически мы можем избавиться от хеш-значения этого убранного из подсчёта символа, умножить полученное значение на основание, чтобы восстановить правильный порядок степени предыдущих нетронутых символов, и добавить значение нового символа.

То есть мы можем вычислить хеш новой подстроки по этой формуле:

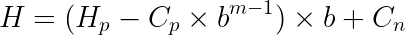
Используя предыдущий пример сдвига от 213 к 135, мы можем подключить эти значения для получения нового хеша:

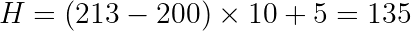
Применяя скользящую хеш-функцию, можно вычислить хеш каждого скользящей подстроки за линейное время. Это основной компонент алгоритма Рабина-Карпа, обеспечивающий лучшее время исполнения O(n+m).

Модулярная арифметика

Результат всех вычислений в рамках алгоритма Рабина-Карпа должен браться по модулю Qво избежание появления больших H (т. е. значений хеша) и целочисленных переполнений. Достигается это, правда, ценой увеличения хеш-коллизий, которые ещё называют ложными срабатываниями.

В качестве значения для Q обычно выбирается простое число  —  настолько большое, насколько это возможно без ущерба для арифметической производительности.Чем меньше значение Q, тем выше вероятность ложных срабатываний.

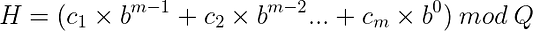
Этот подход таит в себе потенциальную проблему. Чтобы понять, в чём она заключается, рассмотрим простой фрагмент кода JavaScript:

function hash(pattern, Q) {
  const b = 13;
  const m = pattern.length;  let hash = 0;
  for (let i = 0; i < m; i++) {
    const charCode = pattern.charCodeAt(i);
    hash = (hash + charCode * (b ** (m - i - 1))) % Q;
  }

  return hash % Q;
}

Посмотрите: внутри цикла выполняются два умножения и одно сложение. Это не только неэффективно, но и не позволяет предотвратить переполнение целых чисел: выполняется суммирование больших чисел, а до оператора модуля дело даже не дошло. Эту проблему можно решить методом Хорнера.

Метод Хорнера

Метод Хорнера упрощает процесс вычисления многочлена делением его на одночлены (многочлены 1-й степени).

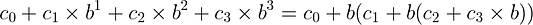
Применив этот метод, мы можем исключить из предыдущей реализации одно умножение. Таким образом, на каждом шаге цикла у нас остаётся только одно умножение и одно сложение, что позволяет предотвратить переполнение целых чисел:

function hash(pattern, Q) {
  const b = 13;
  const m = pattern.length;let hash = 0;
  for (let i = 0; i < m; i++) {
    const charCode = pattern.charCodeAt(i);
    hash = (hash * b + charCode) % Q;
  }

  return hash;
}

Этот же подход можно применить для вычисления скользящего хеша за линейное время:

function roll(previousHash, previousPattern, newPattern, base, Q) {
  let hashCode = previ  // предварительно вычисляем множитель

  let multiplier = 1;
  for (let i = 1; i < previousPattern.length; i++) {
    multiplier *= base;
    multiplier %= Q;
  }  ousHash;  

  // добавляем модуль для получения неотрицательного хэша
  hashCode += Q;  

  hashCode -= (multiplier * previousPattern.charCodeAt(0)) % Q;
  hashCode *= base;
  hashCode += newPattern.charCodeAt(newPattern.length - 1);  
  hashCode %= Q;  

  return hashCode;
}

Сложность

С учётом длины слова m и длины текста n в лучшем случае временная сложность будет составлять O(n + m), а пространственная сложность  —  O(m). Временная сложность в худшем случае будет O(nm). Это может произойти при выборе очень плохо работающей хеш-функции. Решить эту проблему может хорошая хеш-функция, такая как полиномиальный хеш.

Заключение

Несмотря на наличие более производительных алгоритмов поиска одиночных строк, алгоритм Рабина-Карпа может оказаться довольно эффективным при поиске множественных шаблонов. Он обеспечивает прочную основу для расширения вариантов применения в этой проблемной области.

Читайте также:

• Как освоить алгоритмы?
• 10 Графовых алгоритмов
• Графы: основы теории, алгоритмы поиска

Читайте нас в Telegram, VK и Яндекс.Дзен

---

Перевод статьи Vigar Block: Rabin-Karp Algorithm Using Polynomial Hashing and Modular Arithmetic