Графы превратились в невероятно сильное средство моделирования и получения данных из соцсетей, веб-страниц и ссылок, а также определения местоположения и маршрутов в GPS. Любой набор объектов, которые связаны друг с другом, можно сейчас представить с помощью графа.
В статье опишем 10 основных графовых алгоритмов, которые становятся очень полезными для анализа, а также области их применения.
Начнём с того, что приведём определение графа.
Что такое граф?
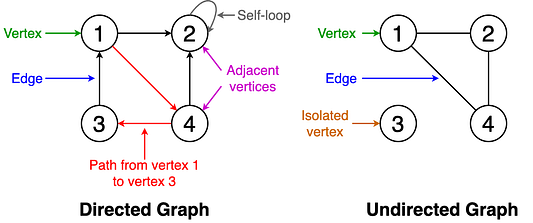
Граф состоит из конечного множества вершин (узлов) и набора рёбер, соединяющих эти вершины. Две вершины считаются смежными, если они соединены друг с другом одним и тем же ребром.
Ниже приведён ряд базовых понятий, относящихся к графам. Они проиллюстрированы примерами на рисунке 1.
- Порядок: число вершин в графе.
- Размер: число рёбер в графе.
- Степень вершины: число рёбер, инцидентных вершине.
- Изолированная вершина: вершина, которая не связана ни с одной другой вершиной графа.
- Петля: ребро, вершины которого совпадают.
- Ориентированный граф: граф, в котором все рёбра имеют направление, определяющее начальную и конечную вершину.
- Неориентированный граф: граф с рёбрами, которые не имеют направления.
- Взвешенный граф: рёбра такого графа имеют определённый вес.
- Невзвешенный граф: рёбра такого графа не имеют никаких весов.
1. Поиск в ширину
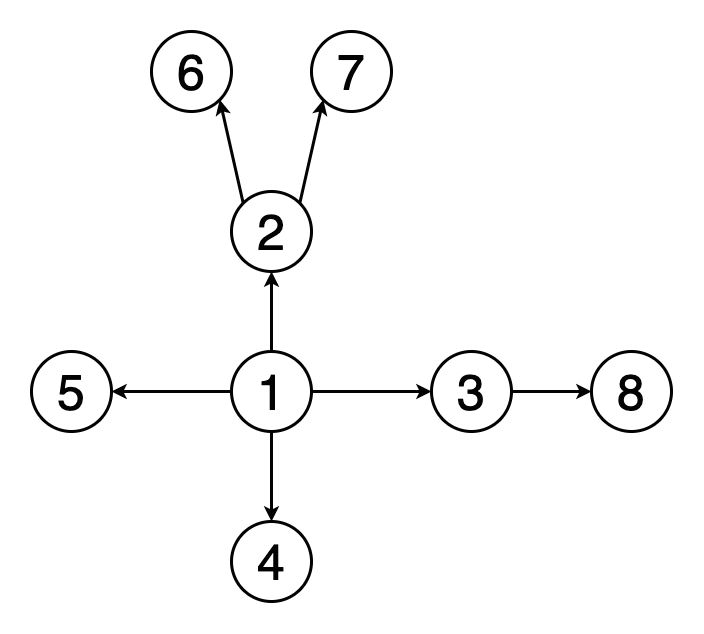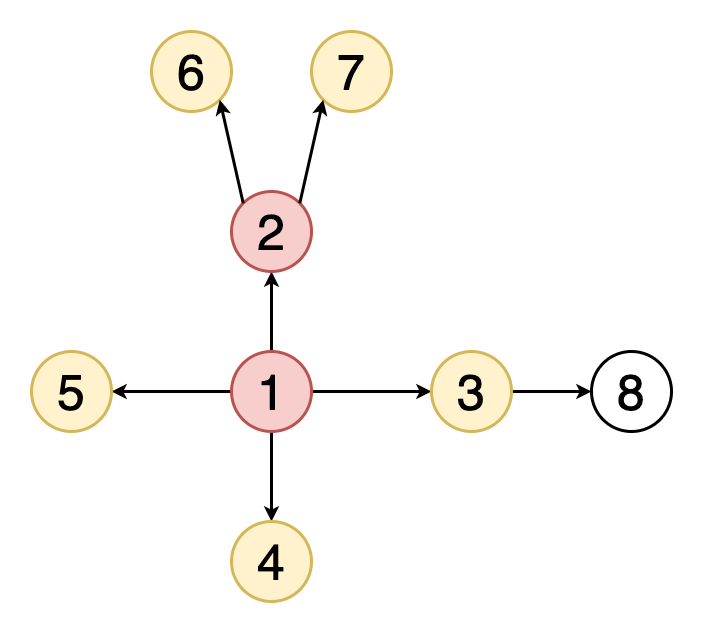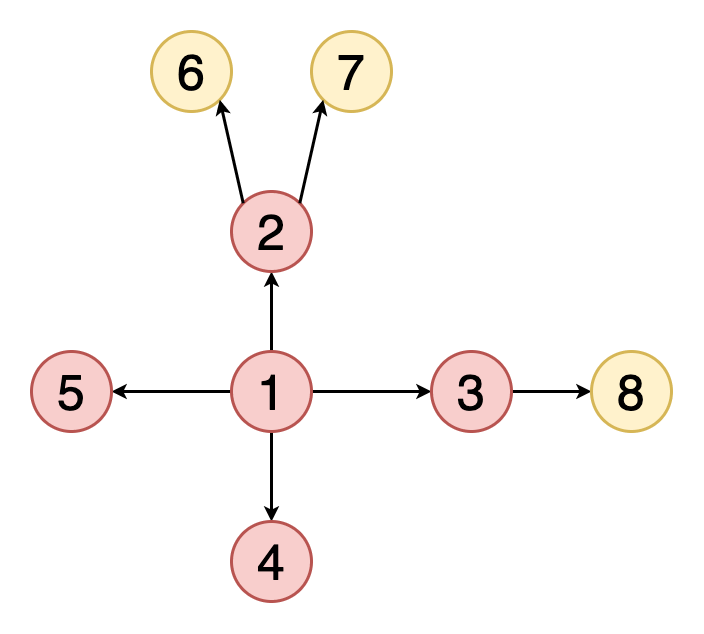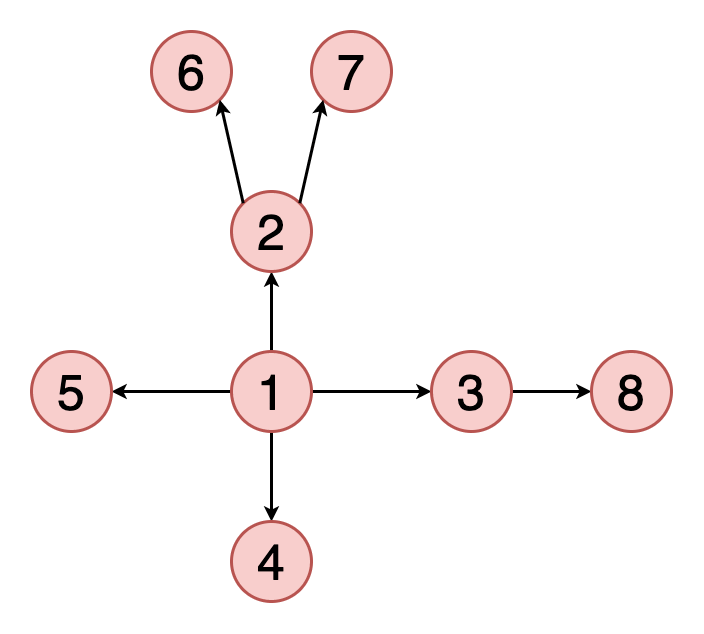
Обход или поиск — это одна из фундаментальных операций, выполняемых на графах. Поиск в ширину начинается с определённой вершины, затем исследуются все её соседи на данной глубине и происходит переход к вершинам следующего уровня. В графах, в отличие от деревьев, могут быть циклы — пути, в которых первая и последняя вершины совпадают. Поэтому необходимо отслеживать посещённые алгоритмом вершины. При реализации алгоритма поиска в ширину используется структура данных «очередь».
На рисунке 2 показан пример того, как выглядит поиск в ширину на графе. Жёлтым цветом помечаются обнаруженные вершины, красным — посещённые.
Применяется для:
- определения кратчайших путей и минимальных остовных деревьев;
- индексации веб-страниц поисковыми ботами;
- поиска в соцсетях;
- нахождения доступных соседних узлов в одноуровневых сетях, таких как BitTorrent.
2. Поиск в глубину
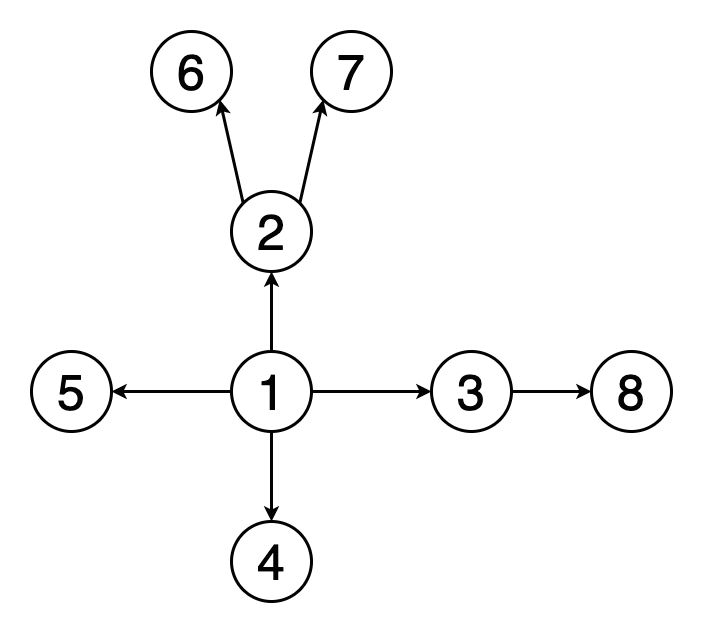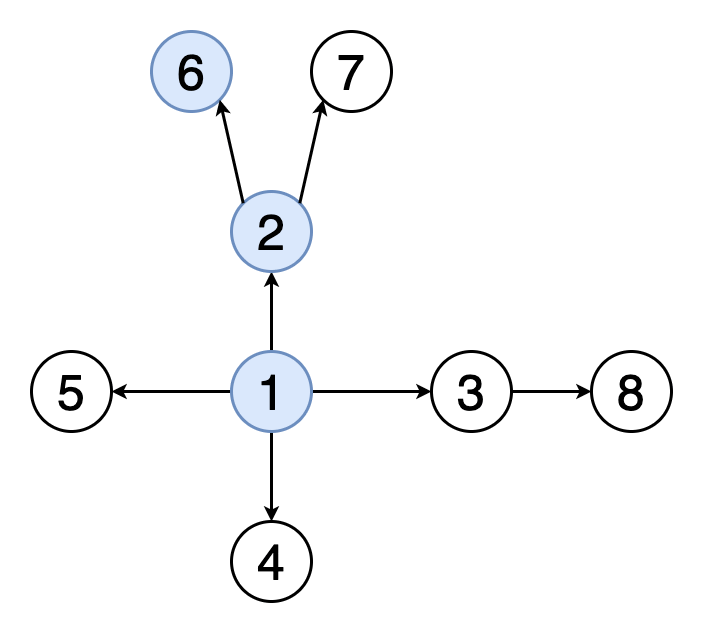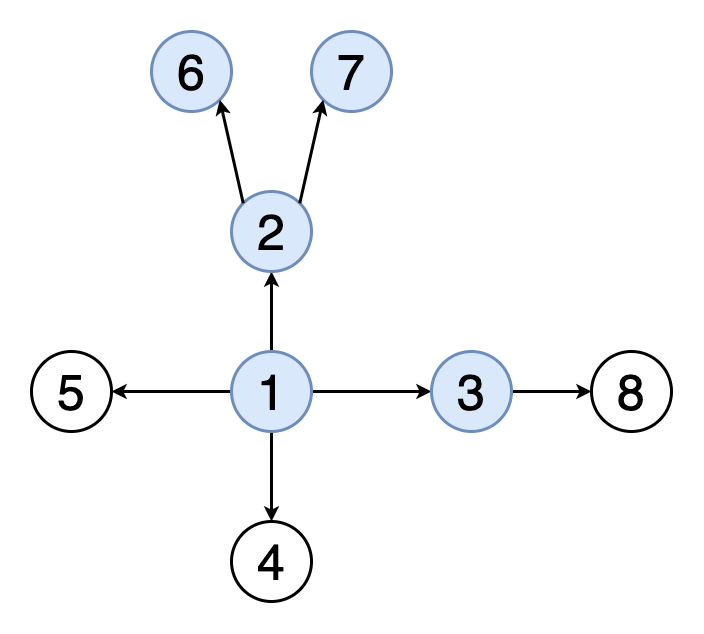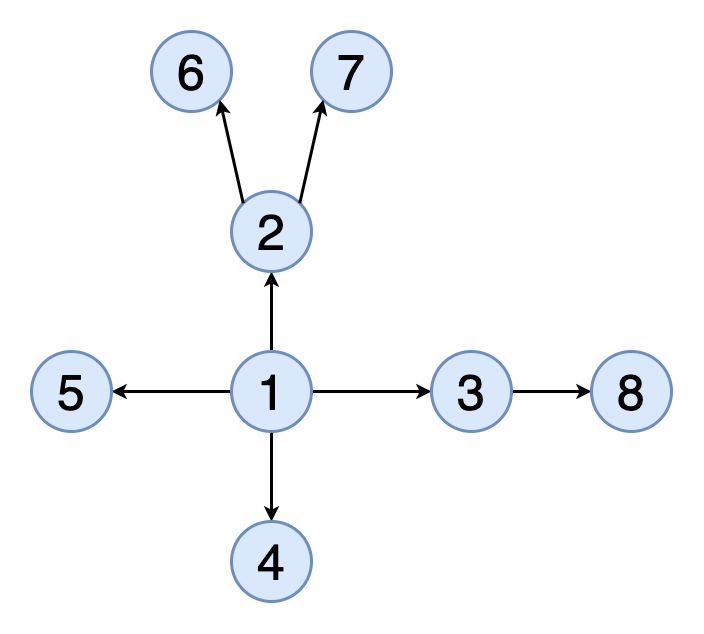
Поиск в глубину начинается с определённой вершины, затем уходит как можно дальше вдоль каждой ветви и возвращается обратно. Здесь тоже необходимо отслеживать посещённые алгоритмом вершины. Для того, чтобы стало возможным возвращение обратно, при реализации алгоритма поиска в глубину используется структура данных «стек».
На рисунке 3 показан пример того, как выглядит поиск в глубину на том же графе, который использован на рисунке 2. Граф обходится на всю глубину каждой ветви с возвращением обратно.
Применяется:
- для нахождения пути между двумя вершинами;
- для обнаружения циклов на графе;
- в топологической сортировке;
- в головоломках с единственным решением (например, лабиринтах).
3. Кратчайший путь
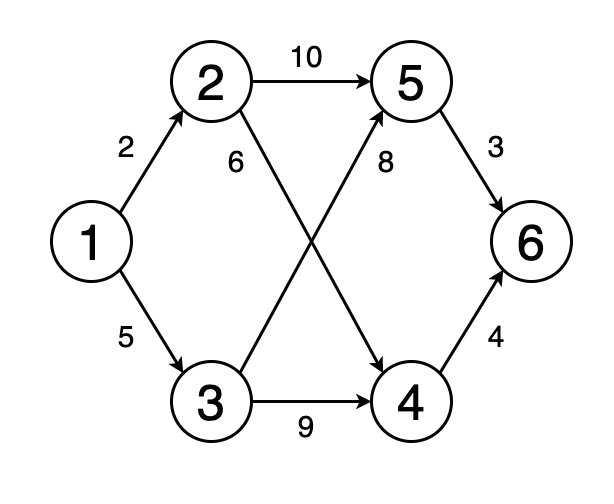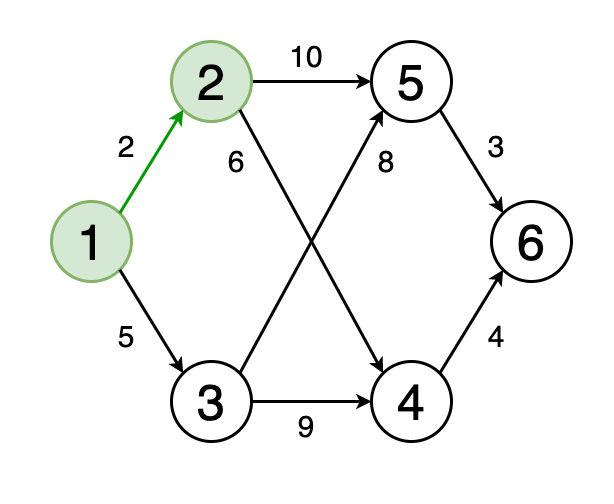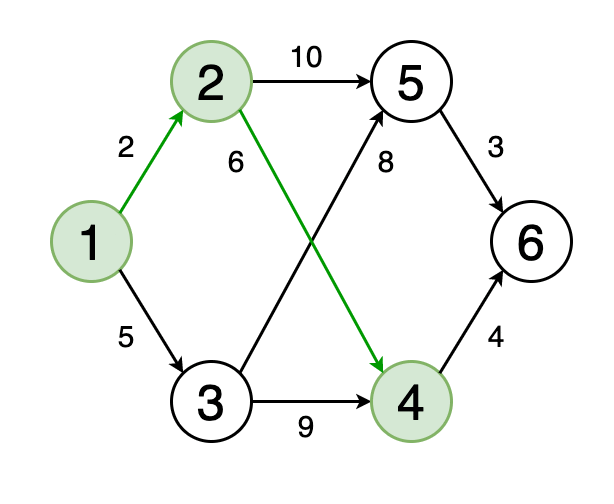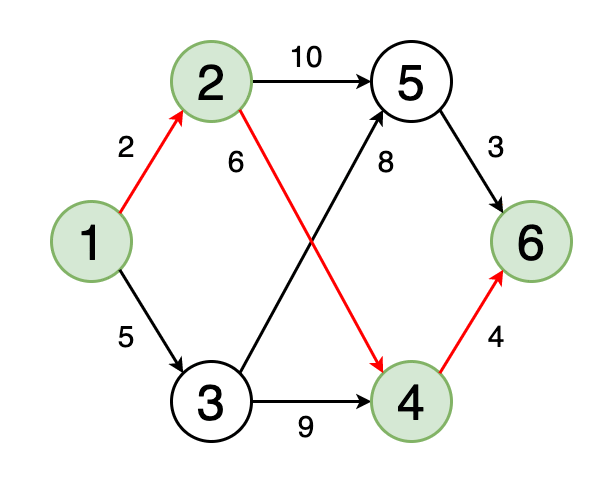
Кратчайший путь от одной вершины графа к другой — это путь, при котором сумма весов рёбер, его составляющих, должна быть минимальна.
На рисунке 4 показан кратчайший путь на графе от вершины 1 до вершины 6.
Алгоритмы нахождения кратчайшего пути:
- Алгоритм Дейкстры.
- Алгоритм Беллмана-Форда.
Применяются в:
- картографических сервисах типа Google maps или Apple maps для прокладки маршрутов и определения местоположения;
- сетях для решения проблемы минимальной задержки пути;
- абстрактных автоматах для определения через переход между различными состояниями возможных вариантов достижения некоторого целевого состояния, например минимально возможного количества ходов, необходимого для победы в игре.
4. Обнаружение циклов

Цикл — это путь, в котором первая и последняя вершины графа совпадают. То есть путь, начинающийся и завершающийся в одной и той же вершине, называется циклом. Обнаружение циклов — это процесс выявления таких циклов. На рисунке 5 показано, как происходит обнаружение цикла.
Алгоритмы обнаружения цикла:
- Алгоритм Флойда.
- Алгоритм Брента.
Применяются:
- в распределённых алгоритмах, использующих сообщения;
- для обработки крупных графов с использованием распределённой системы обработки в кластере;
- для обнаружения взаимоблокировок в системах с параллельным выполнением;
- в криптографических приложениях для выявления ключей сообщения, которые могут соответствовать одному и тому же зашифрованному значению.
5. Минимальное остовное дерево
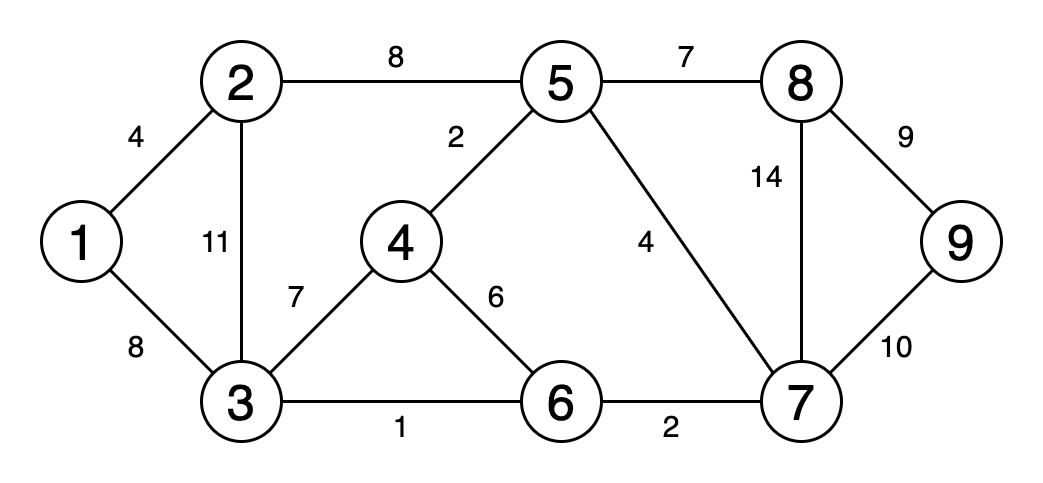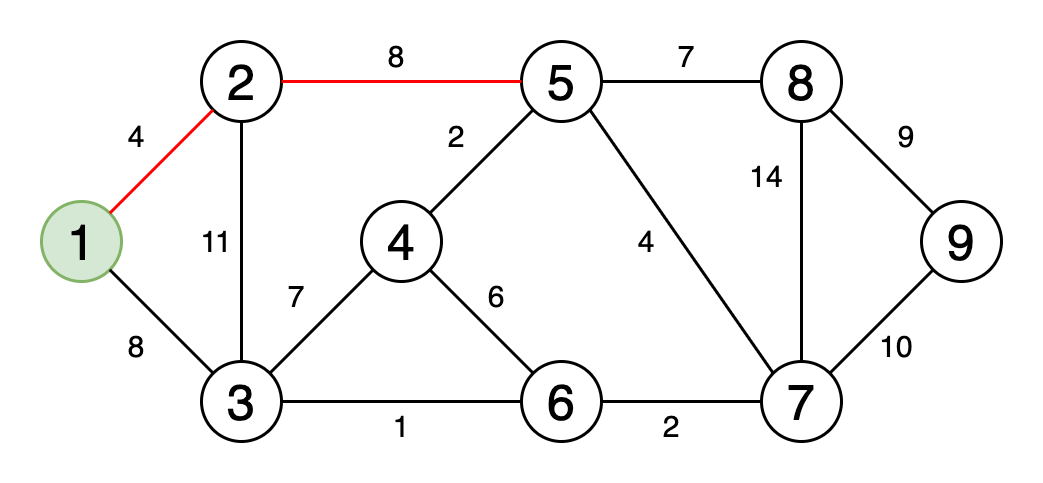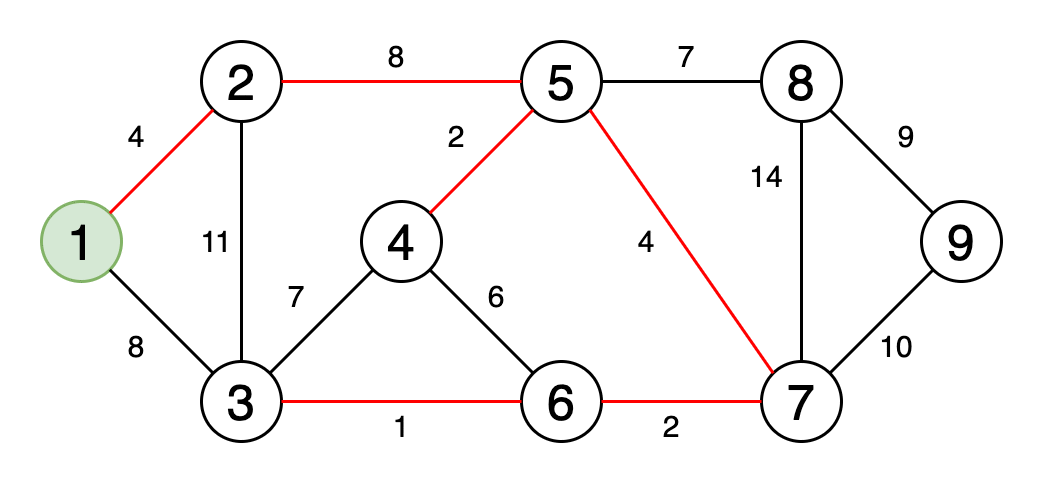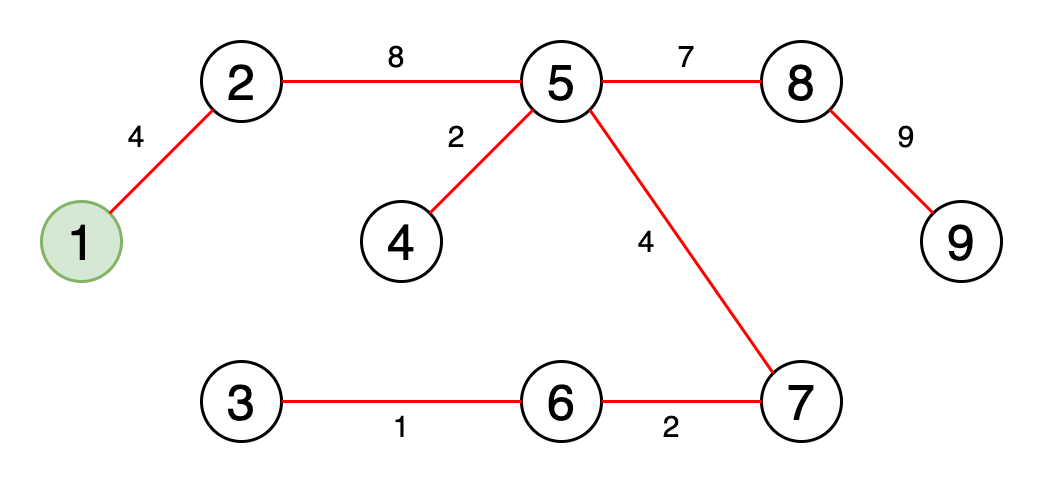
Минимальное остовное дерево — это подмножество рёбер графа, которое соединяет все вершины, имеющие минимальную сумму весов рёбер, и без циклов.
На рисунке 6 показан процесс получения минимального остовного дерева.
Алгоритмы поиска минимального остовного дерева:
- Алгоритм Прима.
- Алгоритм Крускала.
Применяются:
- для создания деревьев для распределения данных в компьютерных сетях;
- в кластерном анализе с использованием графов;
- при сегментации изображений;
- при социально-географическом районировании, когда смежные регионы объединяются.
6. Сильно связные компоненты
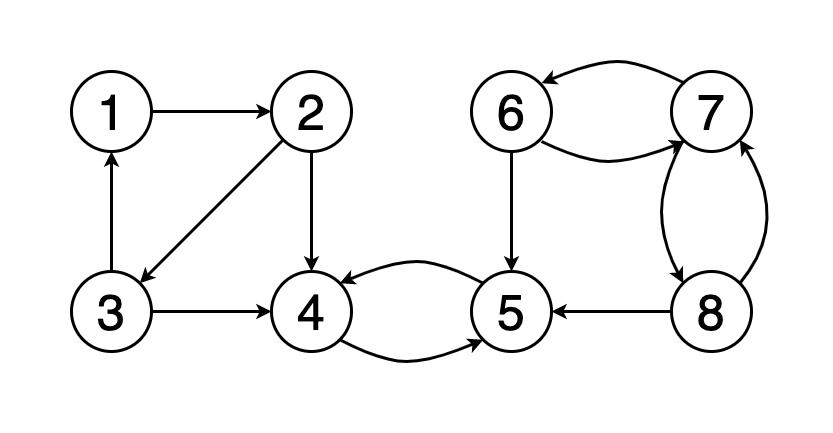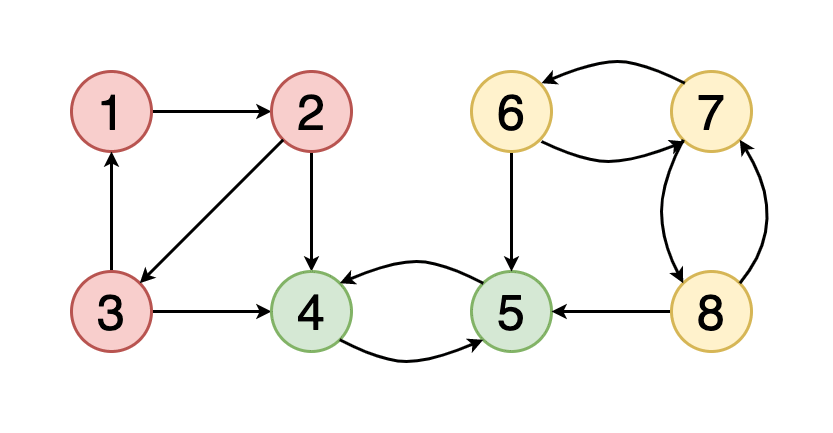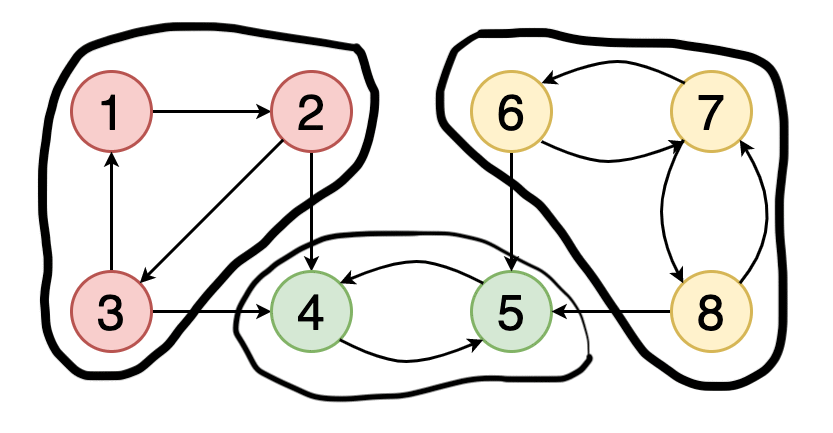
Граф считается сильно связным, если все вершины в графе достижимы из всех остальных вершин.
На рисунке 7 показан пример того, как выглядит граф с тремя сильно связными компонентами, вершины которых окрашены в красный, зелёный и жёлтый цвета.
Алгоритмы поиска сильных компонент связности:
- Алгоритм Косараджу.
- Алгоритм Тарьяна.
Применяются:
- для вычисления декомпозиции Далмейджа-Мендельсона, которая представляет собой разделение вершин двудольного графа на подмножества;
- в соцсетях для поиска групп сильно связанных между собой людей и выдачи рекомендаций на основе общих интересов.
7. Топологическая сортировка
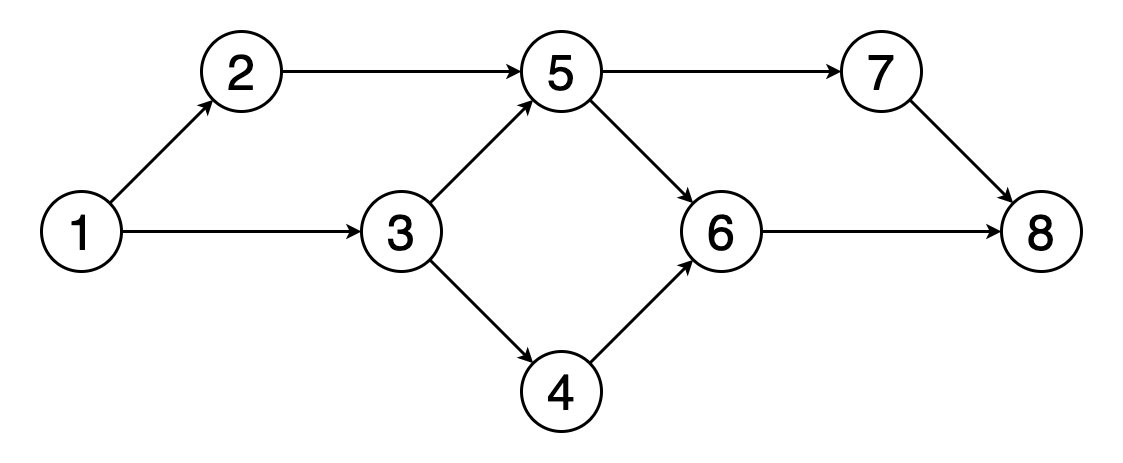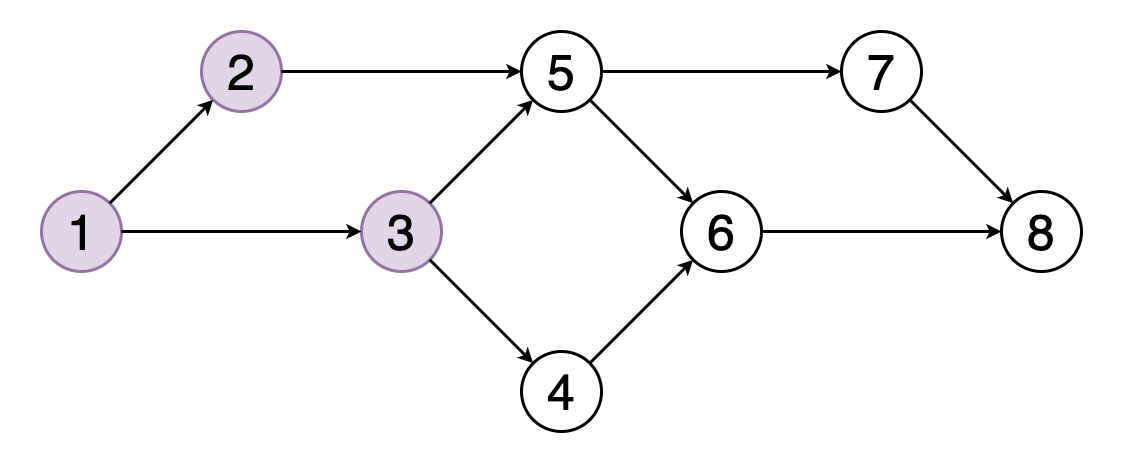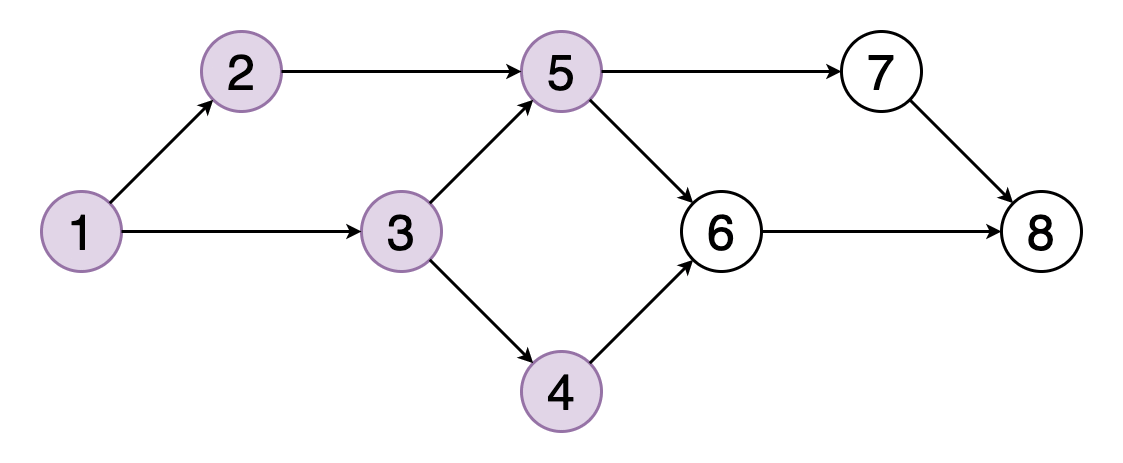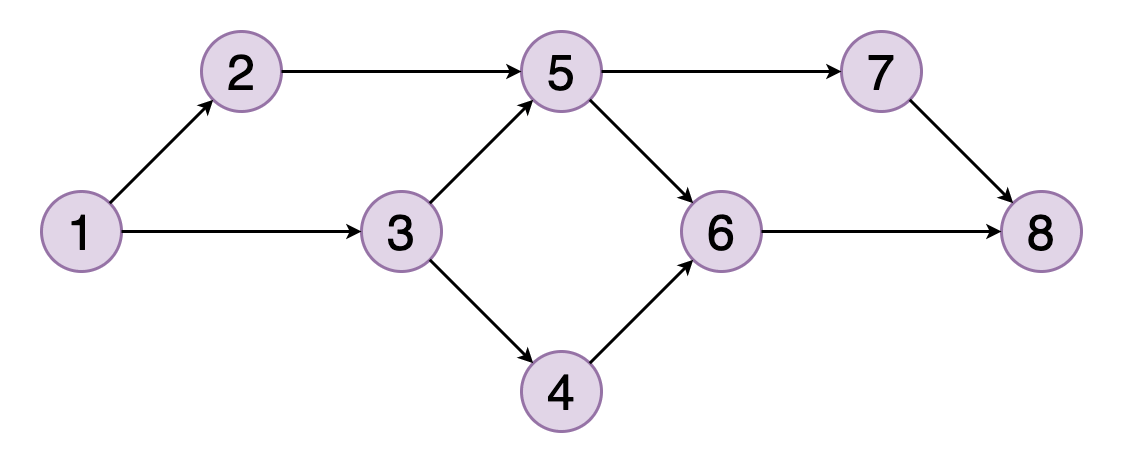
Топологическая сортировка графа — это такое линейное упорядочение его вершин, в котором для каждого направленного ребра, например (u, v), вершина u предшествует вершине v.
На рисунке 8 показан пример топологического упорядочения вершин, согласно которому вершина 5 должна следовать за вершинами 2 и 3, а вершина 6 — за вершинами 4 и 5.
Алгоритмы поиска топологической сортировки:
- Алгоритм Кана.
- Алгоритм на основе поиска в глубину.
Применяются:
- при планировании выполнения команд;
- при сериализации данных;
- определения порядка выполняемых при компиляции задач в Makefiles;
- для разрешения зависимостей символов в компоновщиках.
8. Раскраска графов
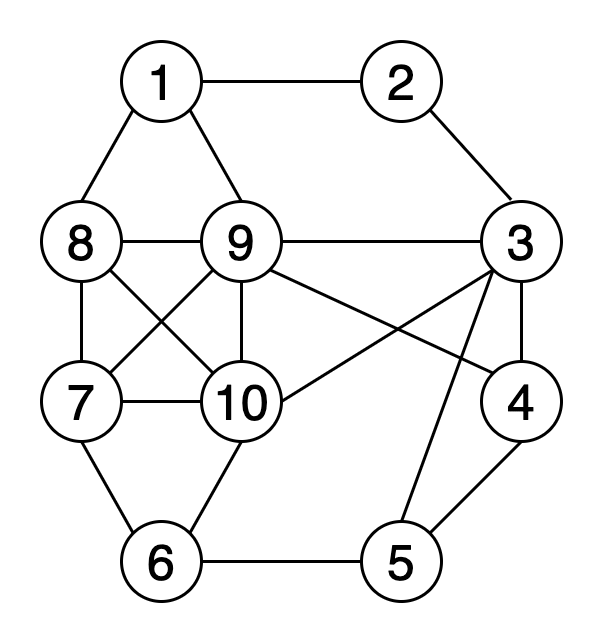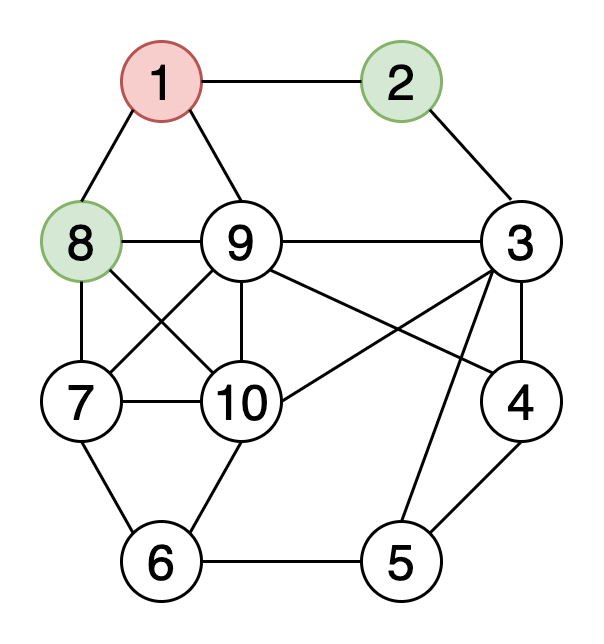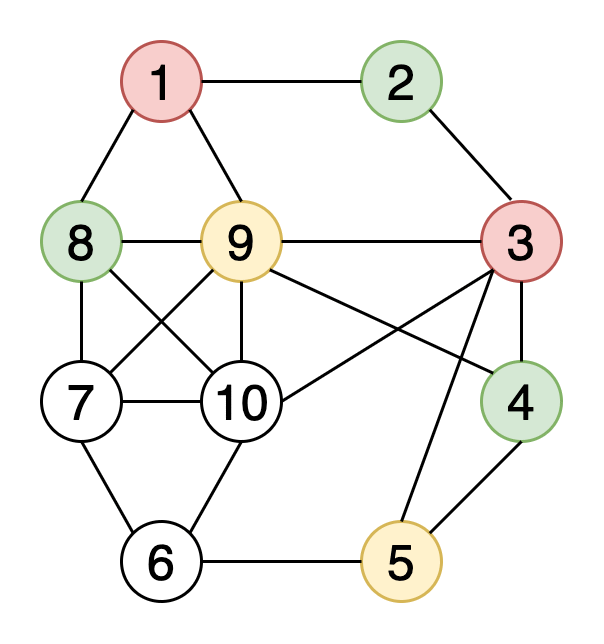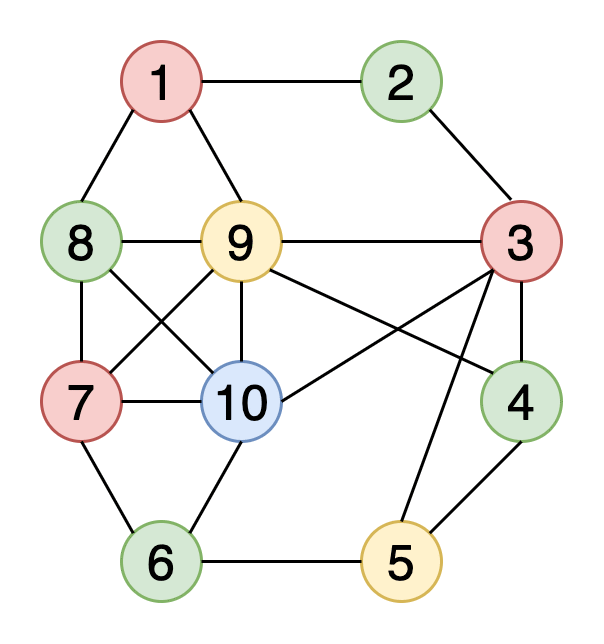
При раскраске графов элементам графа присваиваются цвета с учётом определённых условий. Раскраска вершин — наиболее часто используемый метод окраски графов. При этом вершины графа окрашиваются с использованием k цветов, а любым двум соседним вершинам должны соответствовать разные цвета. Другие методы окраски — раскраска рёбер и раскраска граней.
Хроматическое число графа — это наименьшее количество цветов, необходимых для окрашивания графа.
На рисунке 9 показан пример того, как выглядит раскраска вершин графа с использованием 4-х цветов.
Алгоритмы с раскраской графов:
- Алгоритмы, использующие поиск в ширину или поиск в глубину.
- Жадная раскраска.
Применяются для:
- составления расписаний;
- назначения радиочастот мобильных сетей;
- моделирования и решения головоломок типа судоку;
- проверки того, является ли граф двудольным;
- раскрашивания географических карт стран или штатов, на которых соседние страны или штаты имеют разные цвета.

9. Максимальный поток
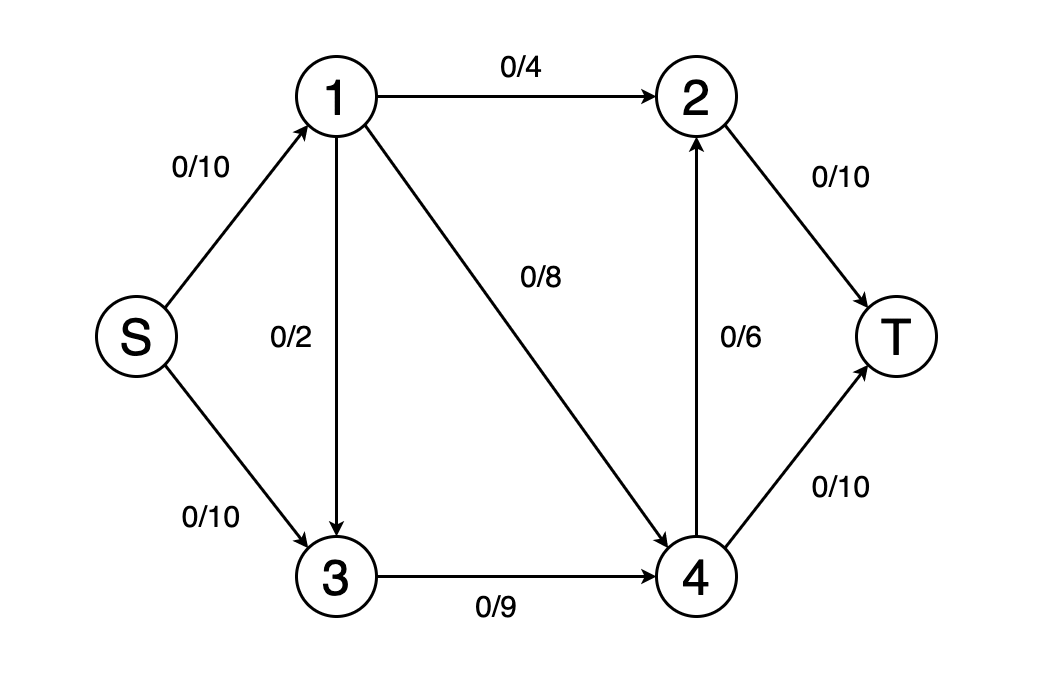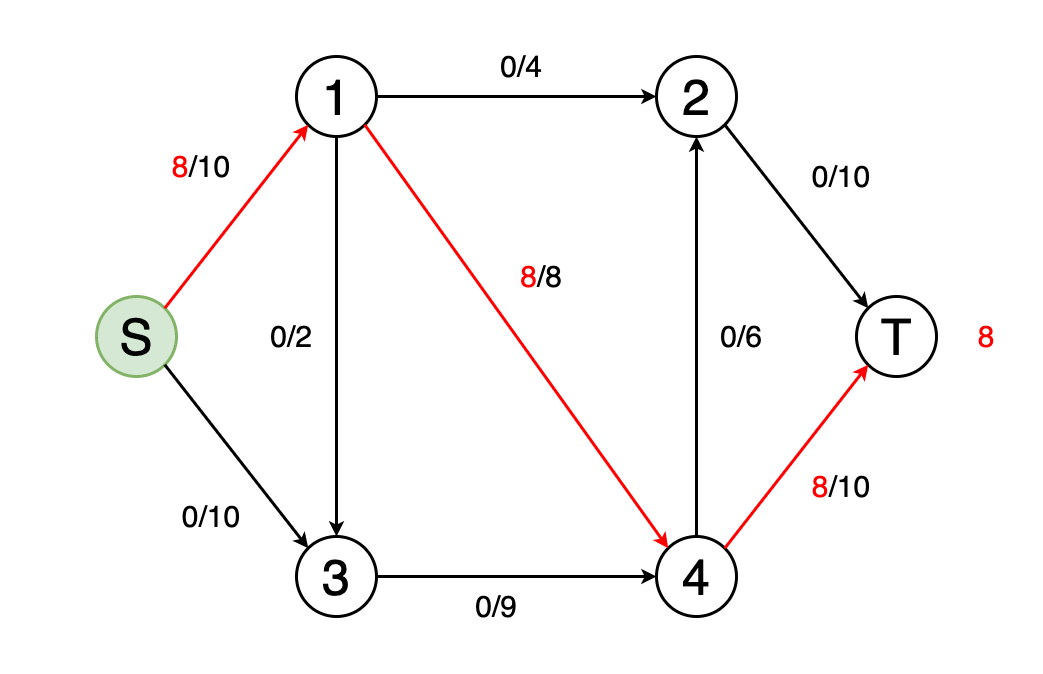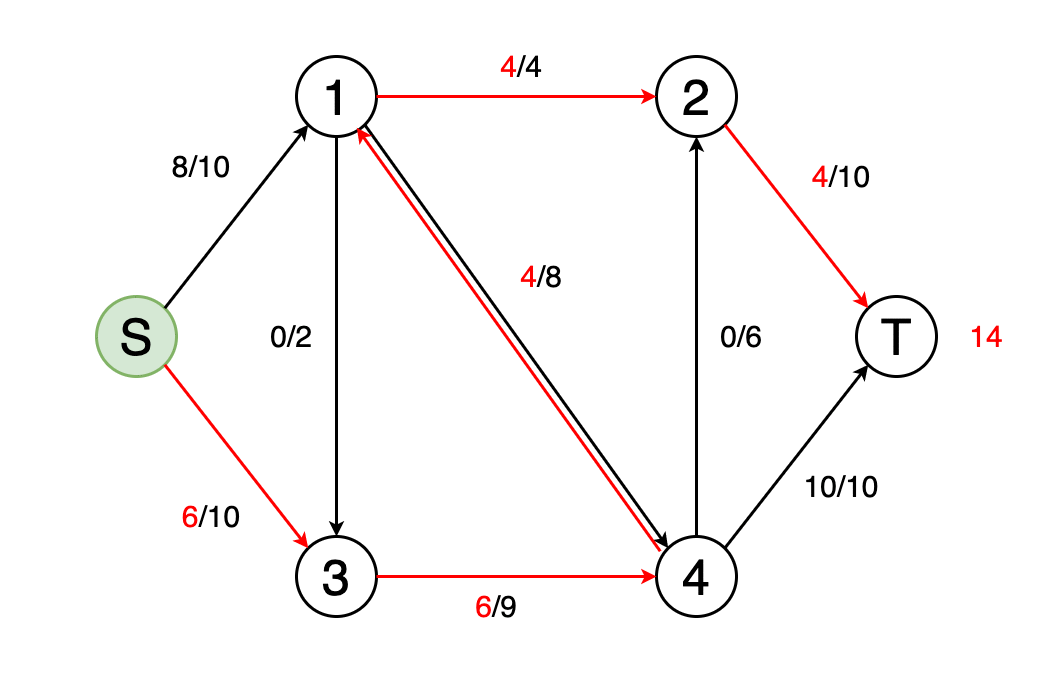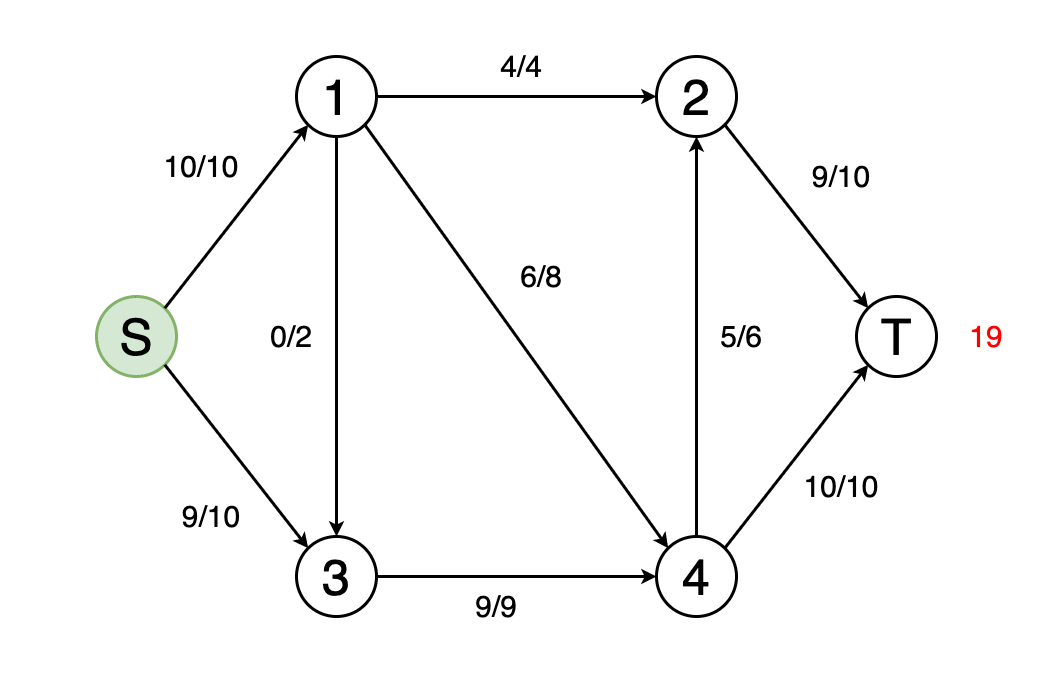
Можно смоделировать граф в виде сети потоков с весами рёбер в качестве пропускной способности этих потоков. В задаче максимального потока требуется найти такой путь потока, который может обеспечить максимально интенсивность потока.
На рисунке 10 показан пример того, как выглядит нахождение максимального потока сети и определение конечного значения потока.
Алгоритмы нахождения максимального потока:
- Алгоритм Форда-Фулкерсона.
- Алгоритм Эдмондса-Карпа.
- Алгоритм Диница.
Применяются:
- в авиакомпаниях для составления полётного расписания экипажей;
- при сегментации изображений для определения фона и переднего плана изображения.
10. Паросочетания
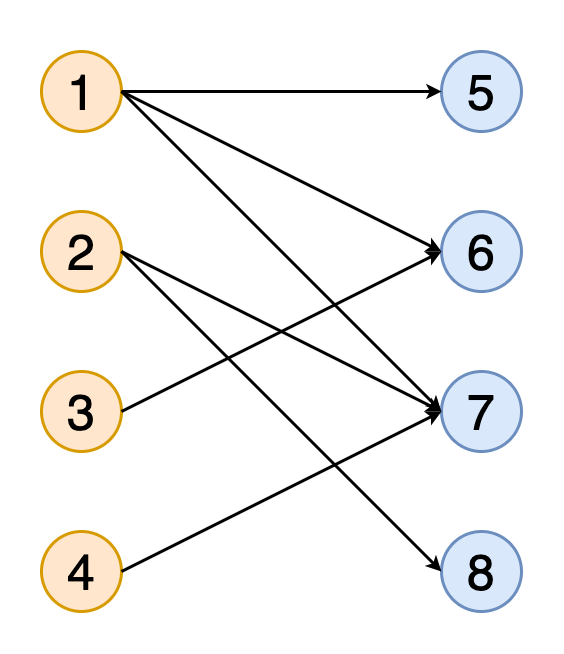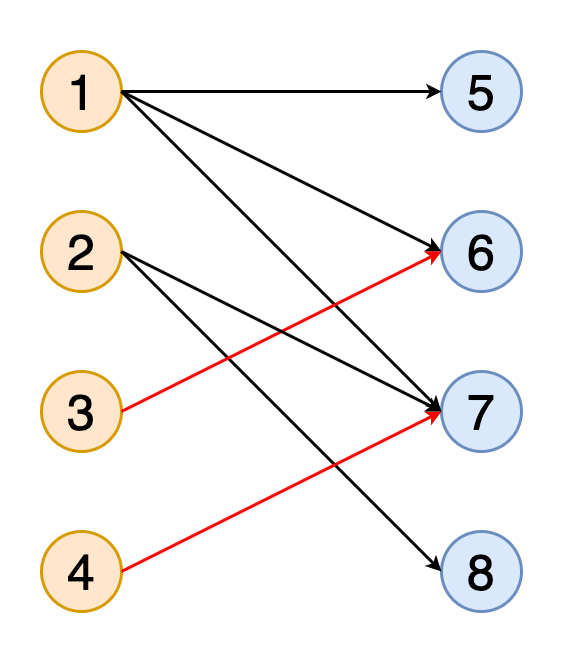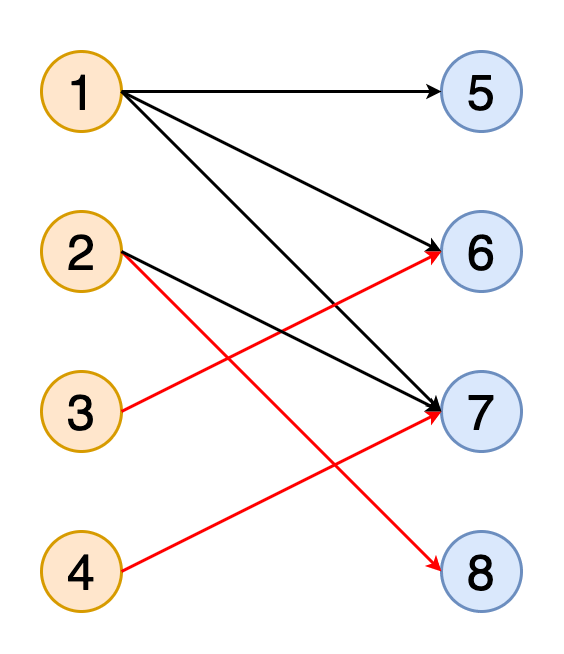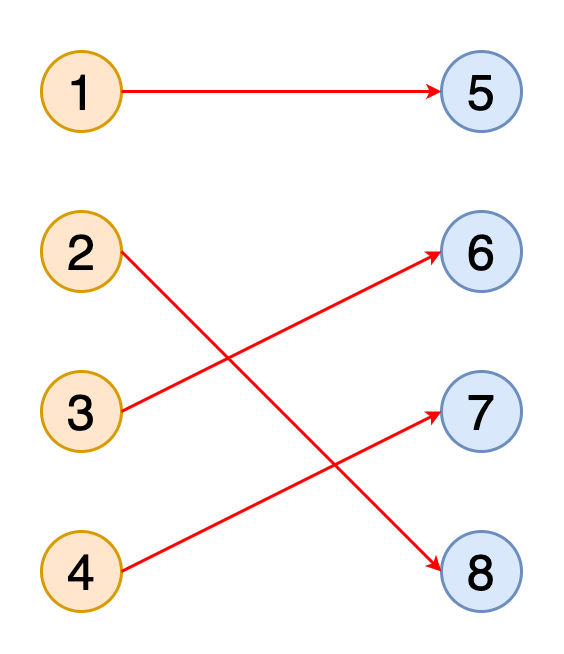
Паросочетание на графе — это набор рёбер, которые не имеют общих вершин (т.е. хотя бы двух рёбер, не имеющих общей вершины). Паросочетание называется максимальным, если оно содержит максимально возможное число рёбер, сочетающихся с как можно большим количеством вершин.
На рисунке 11 показано получение полного паросочетания в двудольном графе с двумя наборами вершин, обозначенных оранжевым и синим цветами.
Алгоритмы нахождения паросочетаний:
- Алгоритм Хопкрофта-Карпа.
- Венгерский алгоритм.
- Алгоритм сжатия цветков.
Применяются:
- в подборе пары для жениха или невесты (задача о стабильных браках);
- для определения вершинного покрытия;
- в теории транспорта для решения задачи распределения ресурсов и оптимизации перевозок.
Заключение
Надеюсь, статья была полезной и в простой и краткой форме познакомила вас с графовыми алгоритмами. 😇
А с реализациями графовых алгоритмов можно ознакомиться в модулях на Python networkx и igraph.
Спасибо за внимание. 😊
Читайте также:
- ML-инженер или специалист по обработке данных? (Закат науки о данных?)
- Когда ИИ или машинное обучение неуместны
- 25 наборов аудиоданных для исследований
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Vijini Mallawaarachchi: 10 Graph Algorithms Visually Explained






