Простая и эффективная утилита сжатия данных кодами Хаффмана на Haskell

Реализуем программу сжатия данных примерно в 150 строках Haskell. Она будет использовать кодирование Хаффмана и обрабатывать произвольные двоичные файлы, используя постоянную память для кодирования и декодирования.

План таков:

1. Кратко расскажу, что такое коды Хаффмана и как их можно использовать для сжатия данных.
2. Напишем кодер, способный сжимать текст.
3. Используем этот кодер, чтобы сжать какой-нибудь файл.

Используем ленивые вычисления, чтобы поддерживать постоянный объем расходуемой памяти, сохраняя модульность кода. Хороший пример причины, почему функциональное программирование вообще важно.

Весь код здесь.

Краткий курс по кодам Хаффмана

Идея проста: сопоставьте каждый символ с уникальной последовательностью битов. Выберем битовые последовательности так, чтобы обычные символы отображались в более короткие битовые последовательности, а редкие символы — в более длинные. Сжатие достигается за счет того, что самые распространенные символы используют меньше битов, чем их несжатое представление.

Я говорю здесь «символы», но на самом деле с битами можно сопоставить что угодно: например, целые слова или даже сами битовые паттерны. Но пока не будем переживать об этом и остановимся на символах.

Допустим, у нас есть строка aaab, и хочется сжать ее с при помощи кодов Хаффмана. Мы знаем, что на входе только два символа, поэтому одного бита должно быть достаточно, чтобы отличить, какой из них какой в каждой позиции.

Вот возможное отображение:

Символы	Кодовое слово
a	1
b	0

Таким образом, бинарный результат в кодировке Хаффмана:

1110

Декодер, зная отображение кодирования, может однозначно получить исходный текст.

Результат тоже был неплохим. Мы закодировали в полбайта то, что в UTF-8 занимало бы 4 байта.

Коды без префиксов

Предположим, входные данные: aaabc. Одного бита недостаточно, но, поскольку a встречается чаще всего, мы выберем для него наименьшее кодовое слово. Что-то вроде такого будет работать.

Символ	Кодовое слово
a	1
b	00
c	01

В итоге получается двоичное:

1110001

Декодер снова может однозначно декодировать результат. Но вы, возможно, заметили, что мы не cмогли выбрать любое кодовое слово для b и c.

Если бы кодовое слово b было 10, а не 00, результаты декодирования стали бы неоднозначными! Во что же должна декодироваться последовательность 101? ac или ba?

Чтобы сделать кодирование однозначным, мы должны убедиться, что ни одно кодовое слово не является префиксом другого кодового слова. Это называется кодом без префиксов.

Построение кодов без префиксов

Есть простой способ построить любое количество кодов без префиксов.

1. Поместите все символы в полное бинарное дерево в качестве листьев.
2. Пометьте все правые ветви 1, а левые — 0.
3. Путь от корня описывает кодовое слово каждого символа.

Посмотрите на полное двоичное дерево ниже. Начиная с корня, можно добраться до любого листа:

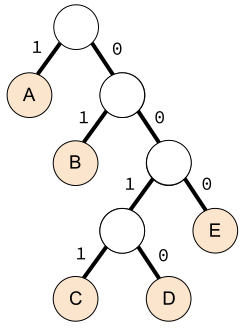
Что описывается этим сопоставлением:

Символ	Кодовое слово
A	1
B	01
C	0011
D	0010
E	000

Мы не должны использовать полное двоичное дерево. Нужно, чтобы символы, которые появляются чаще, располагались ближе к корню. Это даст короткие кодовые слова.

Сделаем следующее: начнем строить дерево снизу. Начнём с самых редких символов, группируя символы с наименьшим количеством вхождений в небольшие деревья. Затем объединяем их так, что самые частые символы добавляются в дерево последними.

Алгоритм:

1. Аннотируем каждый символ, указывая количество вхождений — его вес. Каждый из этих символов станет взвешенным узлом.
2. Сгруппируем в дерево узлы с наименьшими весами. Теперь это дерево стало единым взвешенным узлом, где вес представляет собой сумму двух сгруппированных узлов.
3. Повторяем группировку, пока у нас не будет единого дерева.

Вот как группируется строка aaabc:

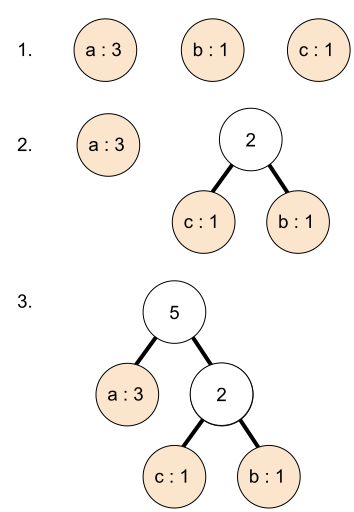
Вы познакомились с кодами Хаффмана! Вы видели, что это такое, как они сжимают данные и как их реализовать.

Пример

Кодируем фразу Try it out with your own content.. Далее — скриншот интерактивного примера в оригинале:

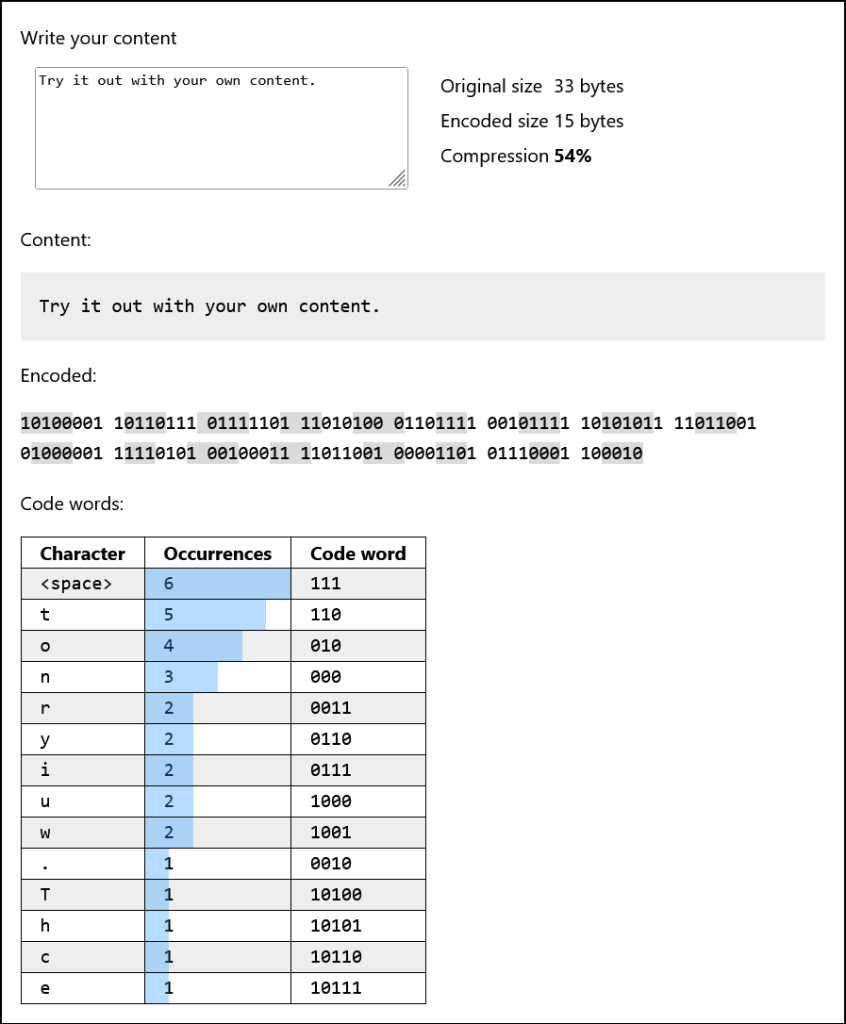
Оригинальный размер	33 байта
Закодированный размер	15 байтов
Сжатие	54%

Содержимое:

T
10100
r
0011
y
0110

111
i
0111
t
110

111
o
010
u
1000
t
110

111
w
1001
i
0111
t
110
h
10101

111
y
0110
o
010
u
1000
r
0011

111
o
010
w
1001
n
000

111
c
10110
o
010
n
000
t
110
e
10111
n
000
t
110
.
0010

Закодированное представление:

10100001 10110111 01111101 11010100 01101111 00101111 10101011 11011001 01000001 11110101 00100011 11011001 00001101 01110001 100010

Кодовые слова:

Символ	Вхождения	Кодовые слова
\<пробел>	6	111
t	5	110
o	4	010
n	3	000
r	2	0011
y	2	0110
i	2	0111
u	2	1000
w	2	1001
.	1	0010
T	1	10100
h	1	10101
c	1	10110
e	1	10111

Пишем кодер

Теперь, когда мы знаем, как происходит кодирование, написать кодер довольно тривиально.

Для начала выделим типы, которые нам понадобятся.

-- import Data.Map.Strict (Map)

data Bit = One | Zero
  deriving Show

-- Кодовое слово
type Code = [Bit]

-- Как часто появляется каждый символ
type FreqMap = Map Char Int

-- Поиск кодового слова для символа
type CodeMap = Map Char Code

-- Как часто в дереве появляются все символы
type Weight = Int

-- Полное двоичное дерево с весом каждого поддерева
data HTree
  = Leaf Weight Char
  | Fork Weight HTree HTree
  deriving Eq

-- Сравниваем деревья по весу, что упростит их построение
instance Ord HTree where
  compare x y = compare (weight x) (weight y)

weight :: HTree -> Int
weight htree = case htree of
  Leaf w _ -> w
  Fork w _ _ -> w

Кодер — это просто функция, которая по заданной строке выводит несколько битов. Но с помощью всего лишь бита декодер не сможет получить исходный текст. Ему необходимо знать применяемое отображение.

Отображение можно построить на основе FreqMap, поэтому будем передавать его, когда кодируем или декодируем что-либо.

Итак, мы хотим написать две функции:

encode :: FreqMap -> String -> [Bit]

decode :: FreqMap -> [Bit] -> String

Кодируем

Начнем с построения FreqMap.

countFrequency :: String -> FreqMap
countFrequency = Map.fromListWith (+) . fmap (,1)

Довольно просто. Как показано ранее, на этом отображении можно построить дерево Хаффмана, так что сделаем это.

-- import Data.List (sort, insert)
-- import qualified Data.Map.Strict as Map

buildTree :: FreqMap -> HTree
buildTree = build . sort . fmap (\(c,w) -> Leaf w c) . Map.toList
  where
  build trees = case trees of
    [] -> error "empty trees"
    [x] -> x
    (x:y:rest) -> build $ insert (merge x y) rest

  merge x y = Fork (weight x + weight y) x y

Вот тут-то и пригодился определённый нами экземпляр Ord. Мы превращаем все символы во взвешенные Leaf. Затем сортируем их, помещая на передний план самые редкие. После этого повторно объединяем передние элементы сортированного списка и снова вставляем объединенный вывод обратно. Функция insert здесь выполняет сортировку вставкой, сохраняя впереди инвариант наименьшей частоты.

Имея дерево Хаффмана, теперь можно просто строить коды!

buildCodes :: HTree -> CodeMap
buildCodes = Map.fromList . go []
  where
  go :: Code -> HTree -> [(Char, Code)]
  go prefix tree = case tree of
    Leaf _ char -> [(char, reverse prefix)]
    Fork _ left right ->
      go (One : prefix) left ++
      go (Zero : prefix) right

Теперь у нас есть все необходимое, чтобы написать encode!

encode :: FreqMap -> String -> [Bit]
encode freqMap str = encoded
  where
  codemap = buildCodes $ buildTree freqMap
  encoded = concatMap codeFor str
  codeFor char = codemap Map.! char

Заметка о ленивой реализации

Шаг, который преобразует исходные входные данные в список битов, — concatMap codeFor str. Концептуально преобразование таково: [Char] в [[Bit]] в [Bit]. Если бы оно происходило так, это стало бы большой проблемой, поскольку нужно было бы сначала закодировать все входные данные, а затем объединить все результаты. Тогда оперативная память должна быть как минимум вдвое больше входной. На самом же деле по мере продвижения малые подсписки слева направо сливаются в большой итоговый.

Это не самый обычный подвиг! Помните, что результатом является неизменяемый (иммутабельный) связанный список. Как можно пройти слева направо, создавая начало списка перед хвостом, не изменяя при этом ни один из его узлов? В этом вся прелесть. Хвост — это параметр thunk: он вычисляется только после того, как мы запрашиваем его значение.

Декодирование

Благодаря этому можно декодировать биты обратно в исходную строку.

decode :: FreqMap -> [Bit] -> String
decode freqMap bits = go 1 htree bits
  where
  htree = buildTree freqMap
  total = weight htree -- сколько символов закодировано
  go count tree xs = case (tree, xs) of
    (Leaf _ char, rest)
      | count == total -> [char]
      | otherwise -> char : go (count + 1) htree rest
    (Fork _ left _ , One  : rest) -> go count left rest
    (Fork _ _ right, Zero : rest) -> go count right rest
    (Fork{}, []) -> error "bad decoding"

Функция go будет проходить по дереву от корня, используя биты входных данных, чтобы решить, влево или вправо идти в каждом узле внутреннего дерева. Когда мы достигаем листового узла, то добавляем к выходным данным символ и снова начинаем от корня.

Это делается, пока не декодируются все символы.

Чтобы узнать, когда остановиться, воспользуемся общим количеством символов total, а не концом входного списка битов, потому что в разделе статьи о сериализации мы добавим кое-какое дополнение в конце для выравнивания на отметке байта.

Обратите внимание, как функция go при достижении Leaf возвращает список, голова которого известна, а хвост представляет собой рекурсивный вызов, что делает go продуктивной. Это означает, что ее результат можно начать вычислять еще до завершения всей рекурсии.

Как и в случае с concatMap во время кодирования, этот дизайн позволит обрабатывать большие входные данные инкрементально. При правильной настройке этим можно воспользоваться для запуска программы, чтобы затрачивать одно и то же [постоянное] количество памяти. Это — следующий шаг.

С этими составляющими уже можно кодировать и декодировать текст методом Хаффмана. Попробуем их в ghci.

$ gchi Main.hs
ghci> input = "Hello World"
ghci> freq = countFrequency input
ghci> bits = encode freq input
ghci> bits
[Zero,Zero,One,Zero,One,One,One,Zero,One,Zero,One,Zero,Zero,Zero,Zero,Zero,One,One,One,Zero,One,Zero,Zero,Zero,One,One,Zero,Zero,One,One,Zero,Zero]
ghci> decode freq bits
"Hello World"

Кодируем двоичные файлы

Можно закодировать входной текст. И всё это хорошо, но как перейти от такого кодирования к кодированию двоичных данных?

Сначала заметим, что ключи отображения представляют всё разнообразие, которое возможно закодировать, каждый элемент с разной частотой. Это символы, но они могли бы быть чем-нибудь другим.

Затем заметим, что конкретный байт — это не более чем один из 256 возможных байтов. Итак, для кодирования двоичных данных нам просто нужно отображение частот байтов (Word8), а не символов.

Но жизнь может быть еще проще. Модулем Data.ByteString.Char8 можно воспользоваться для чтения байтов как Char!

Модуль позволяет манипулировать ByteStrings при помощи операций Char. Все символы будут усечены до 8 бит. Можно ожидать, что эти функции будут работать с той же скоростью, что их эквиваленты у типа Word8 в Data.ByteString.

Это означает, что текстовый кодер можно использовать для кодирования двоичных данных. Не нужно менять код.

Сериализация

Начнем с преобразования вывода в реальные байты, которые можно сохранить в реальном двоичном файле.

Но обратите внимание, что декодер не может просто декодировать поток нулей и единиц без какого-либо контекста. Для этого потребуется отображение частот. Таким образом, сжатый вывод начнется с отображения, за которым следует закодированное содержимое.

Нужна вот эта функция:

serialize :: FreqMap -> [Bit] -> ByteString

Чтобы лениво и эффективно построить ByteString, воспользуемся монадой Put из пакета binary.

-- import Data.Binary.Put (Put)
-- import qualified Data.Binary.Put as Put
-- import Data.ByteString.Internal (c2w, w2c)

serializeFreqMap :: FreqMap -> Put
serializeFreqMap freqMap = do
  Put.putWord8 $ fromIntegral (Map.size freqMap) - 1
  forM_ (Map.toList freqMap) $ \(char, freq) -> do
    Put.putWord8 (c2w char)
    Put.putInt64be $ fromIntegral freqMap

Здесь сначала кодируем длину отображения как Word8. Нужно вычесть единицу, потому что диапазон Word8 — от [0..256), а нам нужно представить диапазон (0…256). Добавим единицу при декодировании, чтобы компенсировать это.

Затем кодируем каждую запись отображения как Word8 как ключ, за которым следует 64-битное целое число — значение.

Благодаря этому можно написать весь код сериализации.

-- import Data.Word (Word8)
-- import Control.Monad (replicateM, forM_, unless)

serialize :: FreqMap -> [Bit] -> ByteString
serialize freqmap bits = Put.runPut $ do
  serializeFreqMap freqmap
  write False 0 0 bits
  where
  write
    :: Bool   -- ^ пишем ли мы маркер конца
    -> Int    -- ^ Биты, заполненные в текущем байте
    -> Word8  -- ^ заполняемый байт
    -> [Bit]  -- ^ оставшиеся биты
    -> Put
  write end n w bs
    | n == 8 = do
      Put.putWord8 w
      unless end $ write end 0 0 bs
    | otherwise =
      case bs of
        (One : rest) -> write end (n + 1) (w * 2 + 1) rest
        (Zero : rest) -> write end (n + 1) (w * 2) rest
        [] -> write True n w $ replicate (8 - n) Zero -- заполнение нулями

В функции write создаем по одному байту, начиная с его самого правого бита. Умножение на 2 сдвигает биты влево, позволяя добавить место для следующего бита.

Пройдя 8 бит, записываем байт и начинаем заново.

В последнем байте дополняем все оставшиеся биты нулями.

Десериализация

Теперь прочитаем, что мы закодировали.

Для отображения воспользуемся дубликатом Put из Data.Binary.Get. Это достаточно просто и ровно обратно тому, что мы делали раньше.

-- import Data.Binary.Get (Get)
-- import qualified Data.Binary.Get as Get

deserializeFreqMap :: Get FreqMap
deserializeFreqMap = do
  n <- Get.getWord8
  let len = fromIntegral n + 1
  entries <- replicateM len $ do
    char <- Get.getWord8
    freq <- Get.getInt64be
    return (w2c char, fromIntegral freq)
  return $ Map.fromList entries

Имея это в виду, десериализуем код. Будем помнить, что ByteString — это ленивая ByteString, созданная путем чтения входного файла.

-- import Data.ByteString.Lazy.Char8 (ByteString)
-- import qualified Data.ByteString.Lazy.Char8 as BS

deserialize :: ByteString -> (FreqMap, [Bit])
deserialize bs = (freqMap, bits)
  where
  (freqMap, offset) = flip Get.runGet bs $ do
    m <- deserializeFreqMap
    o <- fromIntegral <$> Get.bytesRead
    return (m, o)

  bits = concatMap toBits chars

  chars = drop offset $ BS.unpack bs

  toBits :: Char -> [Bit]
  toBits char = getBit 0 (c2w char)

  getBit :: Int -> Word8 -> [Bit]
  getBit n word =
    if n == 8
      then []
      else bit : getBit (n + 1) (word * 2)
    where
      -- Проверка самого левого бита. Байт 10000000 - это число 128..
      -- Биты меньше 128 имеют 0 в крайнем левом бите.
      bit = if word < 128 then Zero else One

Обратите внимание, что для оставшейся части входных данных не используется Get. Причина в том, что хочется, чтобы deserialize возвращала [Bit], который создается лениво.

То есть хочется, чтобы deserialize вернула [Bit] немедленно, но на самом деле этот список представляет собой просто [выражение-задумку] (thunk). У такого подхода есть кое-какие интересные последствия. Например, не следует запрашивать длину этого списка. Если сделать это, прежде чем предоставить нам длину, пришлось бы вычислять весь список.

Если бы мы использовали Get для всех входных данных, у нас была бы группа вызовов getWord8, связанных вместе посредством монадического связывания (>>=). Монады кодируют последовательность, поэтому возврат списка будет последним действием, которое необходимо выполнить, и перед возвратом потребуется обработка всех входных данных.

Наша стратегия потребления программой постоянной памяти заключается в том, что когда нужно записать какие-то выходные биты, обрабатывается следующая часть [Bit]. Это вызывает вычисление небольшого кусочка ByteString, что приводит к чтению соответствующей части входного файла. Затем обработанное содержимое записывается в выходной файл. Поскольку мы не используем [Bit] или ByteString в других частях программы, сборщик мусора сможет освободить память, выделенную для этой части входных данных, которую мы декодировали. Этот процесс повторяется, пока мы не достигнем конца входных данных. Немного читаем, немного пишем, освобождаем использованную память. Таким образом достигается постоянный расход памяти.

Но разве требуемая память не пропорциональна размеру FreqMap? Да, но если мы кодируем байты, FreqMap может иметь не более 256 записей, то есть постоянные накладные расходы (оверхед).

А теперь код целиком

Можно кодировать и декодировать данные, извлекать их из байтовых строк и помещать их туда. Применим программу к реальным файлам.

compress :: FilePath -> FilePath -> IO ()
compress src dst = do
  freqMap <- countFrequency . BS.unpack <$> BS.readFile src
  content <- BS.unpack <$> BS.readFile src
  let bits = encode freqMap content
  BS.writeFile dst (serialize freqMap bits)
  putStrLn "Done."

decompress :: FilePath -> FilePath -> IO ()
decompress src dst = do
  bs <- BS.readFile src
  let (freqMap, bits) = deserialize bs
      str = decode freqMap bits
  BS.writeFile dst (BS.pack str)
  putStrLn "Done."

Обратите внимание, как при сжатии файл читается дважды. Причина в том, что нам нужен один полный проход по файлу для построения отображения и еще один — для кодирования данных с использованием этого отображения. Если бы файл читался только один раз, мы сохранили бы ссылку на него после построения отображения, чтобы можно было передать эту ссылку в encode. Для этого потребуется хранить в памяти весь входной файл!

Прочитав файл дважды, можно освободить память как при построении отображения, так и при кодировании.

Декомпрессия довольно прямолинейна.

Теперь просто обернём программу в простой интерфейс командной строки, и все готово.

-- import System.Environment (getArgs)

main :: IO ()
main = do
  args <- getArgs
  case args of
    ["compress", src, dst] -> compress src dst
    ["decompress", src, dst] -> decompress src dst
    _ -> error $ unlines
      [ "Invalid arguments. Expected one of:"
      , "   compress FILE FILE"
      , "   decompress FILE FILE"
      ]

Поскольку мы используем только пакеты, которые уже поставляются с GHC, нам даже не нужен Cabal, и код можно скомпилировать сразу.

$ ghc -O2 Main.hs -o main

Попробуем с текстовым файлом. Воспользуемся «Войной и миром» Толстого.

# сжимаем
$ ./main compress WarAndPeace.txt WarAndPeace.txt.compressed
Done.

# распаковываем
$ ./main decompress WarAndPeace.txt.compressed WarAndPeace.txt.expanded
Done.

# проверяем, что всё работает
$ diff -s WarAndPeace.txt WarAndPeace.txt.expanded
Files WarAndPeace.txt and WarAndPeace.txt.expanded are identical

# Результат. Уменьшение размера на 40%
$ du -h WarAndPeace*
3.2M    WarAndPeace.txt
1.9M    WarAndPeace.txt.compressed
3.2M    WarAndPeace.txt.expanded

Теперь с двоичным файлом. И чем-нибудь немного больше.

$ time ./main compress ghcup ghcup.compressed
Done.

real    0m15.173s
user    0m15.035s
sys     0m0.077s

$ time ./main decompress ghcup.compressed ghcup.decompressed
Done.

real    0m14.555s
user    0m14.402s
sys     0m0.098s

$ ls -lah ghcup* | awk '{ print $5 "\t" $9 }'
106M    ghcup
84M     ghcup.compressed
106M    ghcup.decompressed

Флаги +RTS -s, покажут, что максимальный размер резидентного набора был менее 300 КБ в случае обработки ghcup, и оба процесса использовали для запуска меньше, чем 10 МБ памяти.

Посмотрите отчет профайлера, чтобы узнать, на что тратится время.

Как сделать лучше?

Есть много способов сделать её эффективнее за счет немного большей сложности.

Вот некоторые улучшения, которые можно попробовать реализовать самостоятельно.

• Многопоточность — параллельное декодирование разделов файла. Поскольку мы не можем определить, где находятся границы кодовых слов в случайном месте файла, в начале сжатого файла можно добавить таблицу, определяющую границы разделов и их ожидаемый декодированный размер, чтобы обрабатывать их параллельно.
• Однопроходное кодирование — построение отображения по ходу работы. Преимущество также заключается в том, что включать её в начало файла не требуется. Вы начинаете с отображения, где каждый байт имеет равное значение частоты, — 1, затем каждый раз, когда вы видите байт, вы сначала кодируете его, а затем обновляете отображение. Декодер делает то же самое: декодирует байт, а затем обновляет отображение. Таким образом, кодер и декодер по-прежнему смогут понять друг друга.
• Каноническое кодирование Хаффмана. Вместо навигации по дереву декодирования за время O(log n), можно использовать код для индексации прямо в векторе за время O(1). Стоит посмотреть вики.
• Ускорение генерации кода. Если вы попробуете однопроходное кодирование, потребуется значительно ускорить создание CodeMap. Более быстрые способы создания кодовых слов позволяют обойтись без построения дерева, как делалось в этом посте.

И вот она. Полезная утилита сжатия данных на Haskell.

Читайте также:

• Форматы .tar .zip .gz: Различия и эффективность
• Монада - программируемая точка с запятой
• Haskell: навстречу функциональному программированию

Читайте нас в Telegram, VK и Дзен

---

Перевод статьи Marcelo Lazaroni: Building a data compression utility in Haskell using Huffman codes