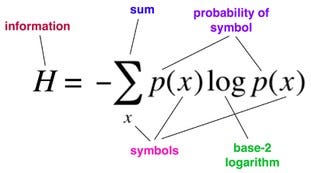Индонезийские пещеры острова Борнео дают представление о самой примитивной зарегистрированной форме коммуникации. Около 40000 лет назад, ещё до развития письменного языка, физические иллюстрации на стенах пещеры были наиболее систематическим зарегистрированным способом общения. С течением времени методология записи эволюционировала от наскальных рисунков до сложных алфавитов, предлагая полноценное выражение с помощью сложной структуры называемой язык. В английском языке идеи, столь же чёткие, как “дерево”, и столь же неоднозначные, как “любовь”, выражаются с помощью 26 букв, не имея никакой внутренней ценности кроме той, которую в них вкладывает общество.
Информация в контексте недавно развившейся области определяется как разрешение неопределённости (или неожиданности). Рассмотрим сообщение о существовании дерева. Например, на фиксированном изображении форма, цвет и даже относительный размер соседних деревьев прекрасно видны, но является ли эта информация предельно точной? Относительно. Несоответствие проявляется только при сравнении с дополнительной информацией, предоставленной письменным языком. С неограниченным запасом слов язык предлагает намного более глубокую описательную информацию, которую невозможно увидеть на изображении, например, где дерево было выращено, кем и в какой почве. Различные методы коммуникации подразумевают различия в сообщаемой неопределённости.
Отец теории информации, математик Массачусетского технологического института Клод Шеннон, блистательно представил логический математический способ измерения этого различия в зарегистрированных методах коммуникации: он определил её как энтропию. Энтропия дополняет математический набор инструментов для измерения взаимосвязи между принципами неупорядоченности и неопределённости. Высокий уровень энтропии указывает на высокий уровень неопределённости информации. Или, на практике, на более высокое число возможных выводов функции. Прежде чем перейти к современной формуле измерения информации, вернёмся назад в 1920–е, когда Ральф Хартли вывел первую формулу на основе работ Генри Найквиста.
Ранняя энтропия — мера неопределённости
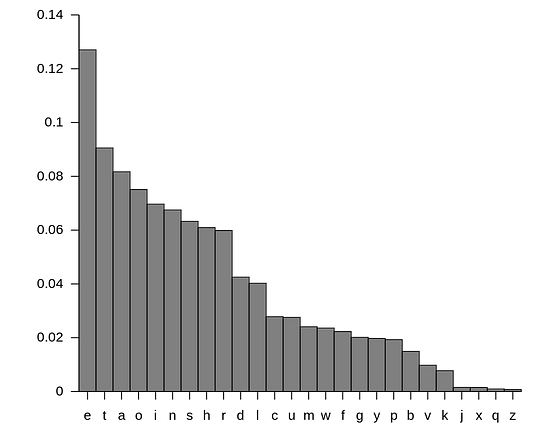
Информация определяется как разрешение неопределённости: если для определения значения не требуется никаких вопросов, то предоставляемой информации не существует. Энтропия напрямую соотносится с информацией системы. Чем выше энтропия, тем больше неопределённости связано с определением символа (числа, буквы и т.д.). Энтропия, или неопределённость, математически максимальна, когда символ может в равной степени иметь множество значений (равномерное распределение). Простейшая единица энтропии — символ, в равной степени способный принимать одно из двух значений. Бросок монеты, например, имеет двоичное свойство — либо орёл, либо решка.
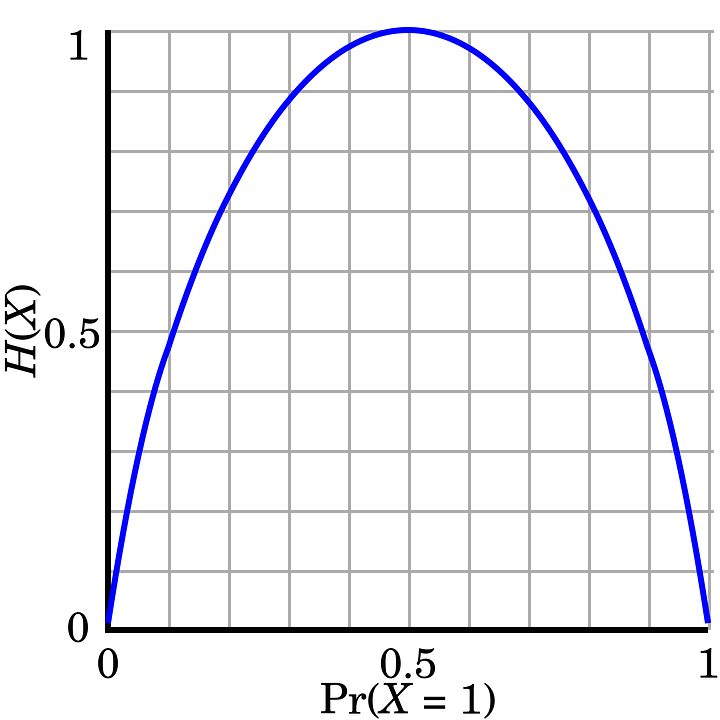
На графике по оси y, H(x), отображается энтропия для символа с двумя возможностями (двоичная). Заметьте, что энтропия, или неопределённость, максимальна (равна 1) в середине графика. Объяснение интуитивно понятно: когда мы бросаем монетку, неопределённость исхода максимальна, когда монета находится в воздухе. Соответственно энтропия минимальна (равна 0) на противоположных концах оси x, когда мы точно знаем значение двоичного символа. Имея это в виду, можно смело утверждать, что подбрасывание монетки, вопросы типа “да/нет”, логические значения и двоичные числа (0 или 1) математически эквивалентны — на графике все они представлены в терминах теории информации.
Символ с двоичным свойством, называющийся “бит”, является базовой единицей энтропии, используемой во всей теории информации.
Хронологически термин “бит” не был общепринятым до довольно позднего времени, однако мы используем его сейчас для простоты понимания, поскольку приближаемся к современной теории информации. Забавный факт: слово “бит” образовано от слов binary digit — двоичное число.
Резонно предположить, что предполагаемое сообщение с решением за один шаг (один бит, бросок монеты, ответ на вопрос типа “да/нет”, логическое значение неопределённости) имеет меньшее значение энтропии, чем решения в два или более шагов. Например, рассмотрим бросок монеты. При попытке определить, выпадет орёл или решка, для разгадки значения “выпал орёл?” достаточно одного бита. В любом случае мы уверены в том, что значение будет получено с первой попытки. Энтропия этой задачи равна единице, поскольку ответ определяется за один шаг:
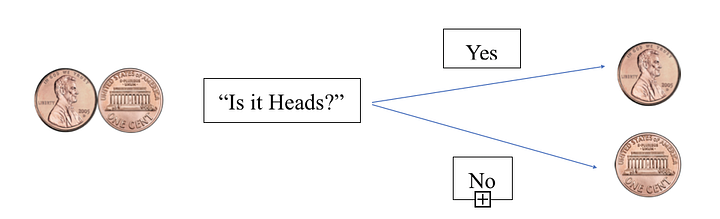
При рассмотрении более сложных проблем потребуется дополнительное количество логических значений, чтобы с уверенностью определить ответ. Теперь мы знаем, что при передаче одного символа простейший символ — бит — обладает энтропией, равной единице.
Что, если отправить сообщение из трёх символов (все биты)?
Продолжая пример выше, скажем, мы хотим отправить трёхсимвольное сообщение из трёх бросков монет. Общее число возможных сообщений теперь равно восьми (2³), но энтропия этого сообщения равна трём. Помним, что энтропия — это не количество возможных сообщений, а минимальное число вопросов, необходимых для определения сообщения.
Что, если отправить сообщение с единственным не двоичным символом?
Теперь, допустим, мы хотим отправить один символ, что означает, что символ может быть любой из двадцати шести букв (1/26). Каково будет значение энтропии на этот раз? То есть, на сколько вопросов типа “да/нет” мы должны ответить, чтобы определить, например, букву J?
Проще всего запрашивать в алфавитном порядке “является ли X предполагаемой буквой?”. Например, “нам нужна А буква? Как насчёт B? Или C?…”. С помощью этого метода для определения одного символа в среднем нам понадобится 13 вопросов типа “да/нет” (или 13 бит энтропии). Однако здесь есть большая оговорка: для измерения информации необходим наиболее эффективный способ присвоения значения символам. В отличие от индивидуального поиска по порядку, мы заимствуем концепцию алгоритма двоичного поиска. При повторном поиске буквы Jспрашиваем, находится ли искомая буква в первой половине алфавита? Да. Далее делим оставшийся массив пополам и спрашиваем, попадает ли искомый символ в первые 6 букв (A-F)? Нет. И так далее, пока не найдём искомый символ — J. Заметьте, что подобный способ поиска значения гораздо более эффективен. В отличие от среднего значения из 13 вопросов “да/нет”, со вторым методом нам никогда не понадобится более 5 вопросов (иногда только 4).
Как следует из этого наблюдения, теоретически количество энтропии увеличивается в два раза для каждого возможного символа в области сообщений. Зная эту взаимосвязь, весьма просто вычислить самый эффективный способ перевода символов алфавита при равномерном распределении:
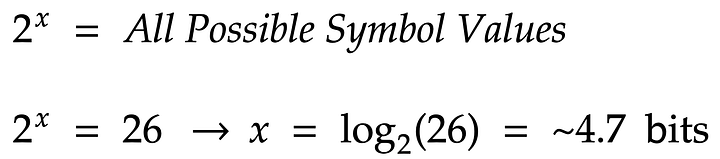
Формула выше даёт приблизительное количество энтропии (4,7 бит), связанное с отправкой одного случайного символа алфавита. Как заключил Ральф Хартли в своей выдающейся статье “Передача информации”:
Что мы сделали, так это приняли за нашу практическую меру информации логарифм числа возможных последовательностей символов
Его раннее определение информации немного отличалось в нотации. Он определил H (информацию) как H = n log (s), где H — это информация, n — количество символов (букв, чисел и т.д.), а s — количество различных символов, доступных при каждой выборке (по сути, длина области сообщений).
Всё ещё не совсем современная теория информации, но мы уже твёрдо установили следующее:
- Теория информации предоставляет способ количественной оценки неожиданностей для коммуникационных событий.
- Энтропия или неопределённость — это мера минимального числа вопросов типа “да/нет”, необходимых для определения значения символа.
- Двоичное число, он же бит, имеет энтропию 1 и, следовательно, является базовой единицей этой области математики.
- Вывели раннюю функцию информации, которая принимает набор равномерно распределённых значений символов.
До этого момента мы предполагали, что каждое значение в наборе символов является случайным образом дискретным, однако на самом деле это целесообразное упрощение. Как мы знаем, реальность не так аккуратна, и значения символов не эквиваленты. Существуют органичные, измеримые модели нашего языка и других форм коммуникации. В качестве быстрого мысленного эксперимента вычислим количество букв “e” в предыдущем предложении. Является ли это распределение равномерным распределением 1/26?
Когда символы не случайны — цепи Маркова
Перенесёмся в 1948 год, когда отец современной теории информации, Клод Шеннон, в своей новаторской работе “Математическая теория связи” предположил, что существуют модели в коммуникации, которые можно использовать для вывода одного и того же сообщения или значения в несколько шагов, то есть битов.
Письменный язык предлагает шаблоны, которые делают следующее значение в последовательности более предсказуемым благодаря предыдущим значениям.
Другими словами, предыдущее значение делает следующее менее неопределённым, то есть уменьшает энтропию. Наилучшим примером является предсказуемость появления буквы ‘U’ после ‘Q’ в английском письменном языке. Если за ‘Q’ следует ‘U’ в 90% случаях, потенциальный выход следующей буквы больше не находится в равновесии со всей системой, он смещается к значению ‘Q’ со скоростью 90%.
Это создаёт систему, в которой следующее значение зависит от предыдущего. Русский математик Андрей Марков вывел это в своём революционном доказательстве, которое назвали в его честь как “Цепь Маркова”. В нём он заявляет, что вероятность будущих значений, зависящая от предыдущих, фиксирована в их вероятности. Он доказал, что в течение непрерывного функционирования системы, результаты будут соответствовать их статистической вероятности.
С учётом зависимости “За ‘Q’ следует ‘U’ с вероятностью 9/10 ‘U’” (P(Xi)), энтропия, или неопределённость появления ‘U’ за ‘Q’, равна H(X) = 0.13 бит. Энтропия любого значения полностью случайного алфавита равна H(X) = 4.7 бит. С этим подходом энтропия уменьшается на поразительные 4.57 бита. Вместо деления алфавита пополам на первом этапе вопрос, разрешающий большинство информационных состояний, будет сформулирован как “Значение равно ‘U’?”. В 90% случаев это будет правдой, а энтропия будет только 1 бит, что позволяет убрать лишние вопросы и понизить общую энтропию системы. Благодаря компьютерному анализу миллионов текстов, были выведены стандартные распределения каждой буквы английского языка. Это стандартные вероятности, которые можно использовать для независимых событий. Принимая во внимание зависимые выходные значения (цепь Маркова), были установлены также частотные зависимости повторения букв.
Повторный вывод формулы информации/энтропии
Шеннон модернизировал теорию информации, развивая функцию Хартли. Для набора случайных равномерных значений X мы вычисляем энтропию кодирования единичного символа с помощью log от X по основанию 2. Для набора взаимосвязанных значений X мы вычисляем энтропию единичного символа, складывая индивидуальные значения энтропии для каждого индивидуального возможного значения символа в наборе:
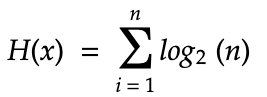
Однако вышеприведённая формула предполагает равномерное распределение, что, как мы знаем благодаря цепи Маркова, не является истиной. Чтобы учесть это, в формулу нужно добавить умножение на частотную вероятность каждого значения символа x, (p(x)):
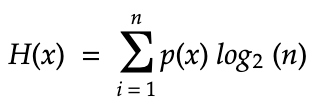
Наконец, нужно заменить n внутри логарифма. Мы рассчитываем количество вопросов типа “да/нет”, необходимых для получения каждого отдельного символа, а не общего результата. Продолжая пример с алфавитом, мы знаем из цепи Маркова, что для угадывания символа e или z требуется неравное количество битов. Следовательно, для каждой суммы нам нужно число конкретных результатов, и мы знаем, что это не 26, а (1 / p(x)):
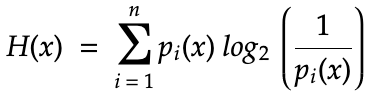
Формула, которую мы только что вывели — это формула, выведенная Клодом Шенноном и сделавшая его отцом теории информации. Он немного переставил символы выше. Вот это уравнение лежит в основе современной теории информации:
H(x) — это энтропия, мера неопределённости, связанная с установленной переменной X. P(x) — это вероятность вывода x в переменной X. И log(1/p(x)) по основанию 2 — это количество битов, необходимое для расшифровки вывода x переменной X. Ещё раз: базовая единица, которой равна H(x), определяется в битах.
Теоретически обновлённая формула Шеннона, использующая принцип цепей Маркова, должна снижать энтропию в наборе значений символа, поскольку мы ушли от равномерного распределения.
Напомним, что мы рассчитали энтропию H(x) = 4.7 для единичного символа алфавита. Давайте сравним ее с H(x), вычисленной по обновлённой формуле:
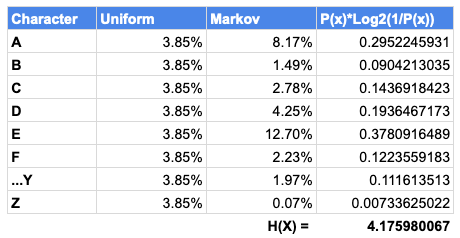
Как видим из суммы справа внизу, это интуитивное значение проверяется итоговым значением энтропии H(x) = 4.18. Уже с этой формулой энтропии теория информации и её приложения развиваются всё быстрее с 1950-х.
Посмотрим на приложения
Изученные здесь концепции, построенные на математическом понятии, узнаваемы и мощны в цифровую эпоху. Вероятно одним из наиболее распространённых и влиятельных применений теории информации является сжатие информации без потерь. Эта форма сжатия используется в записях баз данных, текстовых файлах, изображениях и видеофайлах. В этой форме данные можно полностью восстановить до исходного состояния. Используя принципы энтропии Шеннона и цепи Маркова,можно получить безошибочную информацию. Эта способность к сжатию позволила массово производить устройства, способные хранить огромные объёмы данных. Особенно впечатляет это в музыкальных файлах. В ранние годы звукозапись опиралась на виниловые пластинки — несжатый формат информации. Запись на пластинке хранит альбом в несжатом состоянии без потерь. С современными технологиями музыкальные файлы сжимаются и содержат биты, относящиеся к высоте, громкости, резонансу и т.д. Другой убедительный пример — это увеличение возможностей аппаратного хранения.
Цифровая эпоха могла быть далёкой мечтой без вклада Шеннона в мир связи. Подобно любому другому недостаточно признанному математическому принципу, теория информации играет жизненно важную роль в наших повседневных функциях.
Читайте также:
- Настройка Data Science окружения на вашем компьютере
- Как составить Data Science портфолио? Часть 1
- Реализация base64 на Rust
Перевод статьи Jesus Najera: Intro To Information Theory