Двоичное дерево — это древовидная структура данных, в которой каждый элемент имеет не более 2 дочерних элементов. Эта структура данных состоит из трех основных элементов:
1. Данные
2. Указатель на левый дочерний узел
3. Указатель на правый дочерний узел
Двоичное дерево поиска — это структура данных двоичного дерева, основанная на узлах, которая обладает определенными свойствами, позволяющими более эффективно выполнять такие операции, как поиск и нахождение максимальных или минимальных значений. Свойства выглядят следующим образом:
- Левый потомок и левое поддерево узла содержат только узлы с ключами меньше ключа основного узла.
- Правый потомок и правое поддерево узла содержат только узлы с ключами больше ключа основного узла.
- Поддеревья также должны быть бинарными деревьями поиска.
- Не должно быть дубликатов узлов.
Говоря простым языком, начиная с вершины дерева (корня), левый узел будет меньше корня, а правый будет больше. Следовательно правое поддерево узла будет содержать ключи больше, а левое, наоборот, меньше.
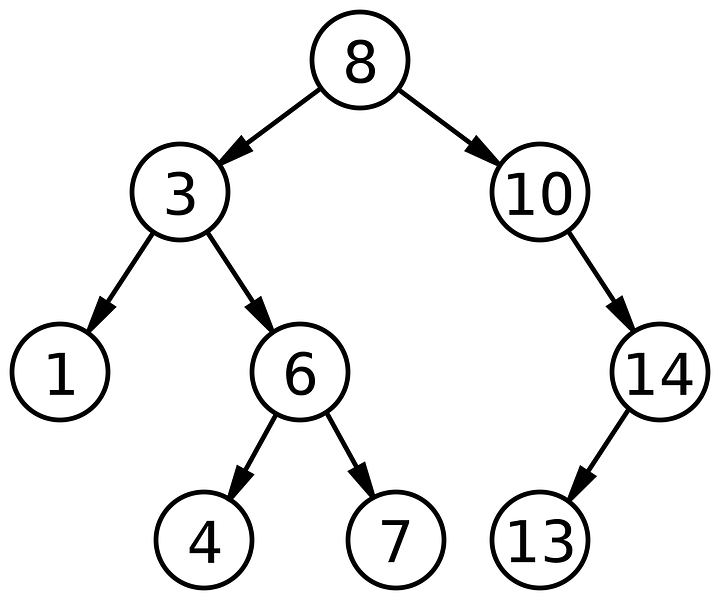
Скажем, узел бинарного дерева был определен таким образом:
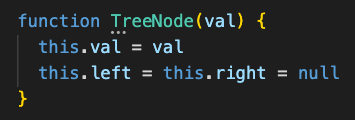
Имея двоичное дерево и некое значение, для того чтобы его вставить, понадобится начать с корня дерева. Мы берем значение корня и сохраняем его в переменную, чтобы сравнить его с заданным значением.

Используя цикл while, мы проходим по дереву, сверяя значение со значением текущего узла. Если значение больше, чем узел, мы проверяем, существует ли правый потомок узла. Если он не существует, мы создаем новый узел, который является правым дочерним элементом текущего. Если же он существует, то мы устанавливаем “текущее” значение как значение текущего узла, на котором мы находимся, и продолжаем перебирать значения дерева. Этот же процесс будет верен, если вставляемое значение меньше, чем узел, только теперь мы будем проверять вместо правого левый дочерний элемент.
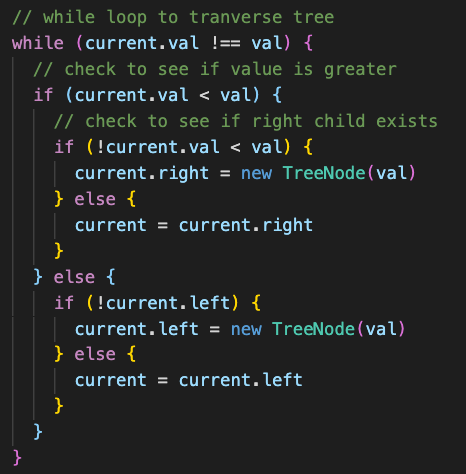
Цикл while будет прерван, как только будет создан новый узел и текущее значение будет таким же, как и заданное значение. Вот эта функция в полном объеме:
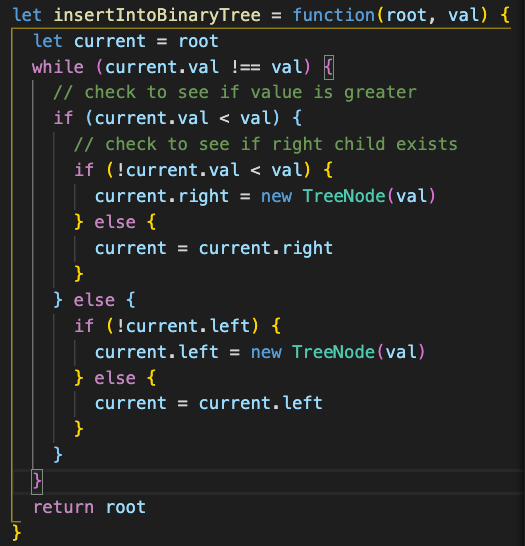
Возможна и другая реализация, включающая рекурсию:

Логика та же, но вместо сохранения текущего узла, на котором мы находимся, в переменную, мы просто снова вызываем функцию и передаем узел и значение, которое хотели бы вставить.
Читайте также:
- Чистый код JavaScript: обработка ошибок
- Да не нужен вам фреймворк JavaScript!
- Создание тестового фреймворка JavaScript
Перевод статьи Jacky Feng: Binary Search Tree: Inserting a Value Using JavaScript






