Рекуррентная нейронная сеть с головы до ног

Нейрон — строительный элемент человеческого мозга. Он анализирует сложные сигналы за микросекунды и отправляет ответы нервной системе, которая решает сложные задачи. У всех нейронов одна и та же архитектура. Это значит, что структурные слои у них одинаковые. Если расположить такие слои последовательно, то можно воссоздать копию нашего мозга. Эти последовательные “слои” помогают нам заниматься рутинными делами, принимать сложные решения и понимать речь друг друга. Вопрос в том, как решить нашу задачу при помощи всех этих слоёв. Какое должно быть моделирование в этом случае?

Ответ на этот вопрос кроется в обмене параметрами. Именно так получится расширить и применить модель к данным разных форматов. А еще можно реализовать обмен данными вывода в виде функции от данных предыдущего вывода. Элементы вывода генерируются по такому же правилу обновления. Самый простой способ понять структуру этих вычислений — использовать ‘Unfolding computational graphs’ (Развёртывание вычислительных графов). Результат этой процедуры: добавление структуры глубокой сети параметров. 

Рассмотрим классическую форму динамической системы:

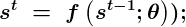
Разворачивая структуру этой динамической системы, получаем:

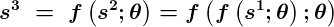
Как мы видим, в уравнении больше нет рекурсии.

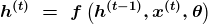
Рекуррентные нейронные сети можно создавать разными способами. У некоторых из них могут быть скрытые узлы. Когда рекуррентная нейросеть обучается работать на прошлых вводных данных с потерями, мы отображаем последовательность произвольной длины на вектор h(t). В зависимости от того, какую задачу мы решаем, мы также можем выбирать, в каком из прошлых вводов можно выборочно оставить некоторые аспекты предыдущей последовательности. 

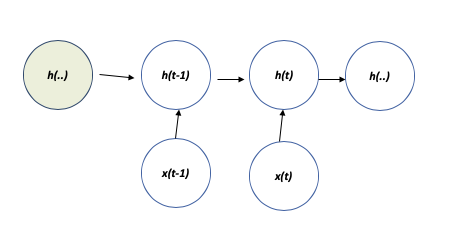
Развёрнутый граф: рекуррентная сеть без выходов. Она обрабатывает информацию со входа x путём включения ее в состояние h, а со временем продвигается далее. 

Мы можем представить развёрнутую рекурсию после t шагов с помощью функции g(t).

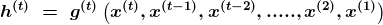
Функция предыдущей последовательности принимает за вводные данные g(t). У процесса развёртывания есть некоторые главные преимущества. Он приводит к событиям, которые позволяют создать модель повсеместной f с последующим обобщением. 

a) Вне зависимости от длины входной последовательности, у модели всегда один и тот же размер входных данных.

b) Реально пользоваться той же функцией перехода f, с теми же параметрами на каждом шагу, потому что они между собой разделены состояниями. 

Развёрнутый граф иллюстрирует идею точного описания и информационного потока. Оба потока вперед и обратно проходят вовремя, показывая прямой путь поступающей информации. 

Эти идеи были важны для того, чтобы построить рекуррентную нейронную сеть (РНС), так как РНС производит выходные данные на каждом этапе и ее соединенные скрытые узлы могут производить выходные данные, считывая всю последовательность, и затем приводить всё к единственному выводу. Таким образом, любую функцию, которую можно вычислить при помощи машины Тьюринга, можно также вычислить и при помощи рекуррентной нейросети конечного размера. 

Такова природа применения предыдущих выходных данных, соединений к скрытым слоям, которые привели РНС к успешному результату в нашем опыте. 

Рекуррентная нейронная сеть

Со знанием того, как разворачивать граф и обмениваться параметрами, мы можем запрограммировать РНС. Мы предполагаем, какой будет функция активации гиперболического тангенса. Естественный способ взглянуть на выходные данные — открыть ненормализованный лог вероятностей. Мы применяем softmax как прием пост-обработки.

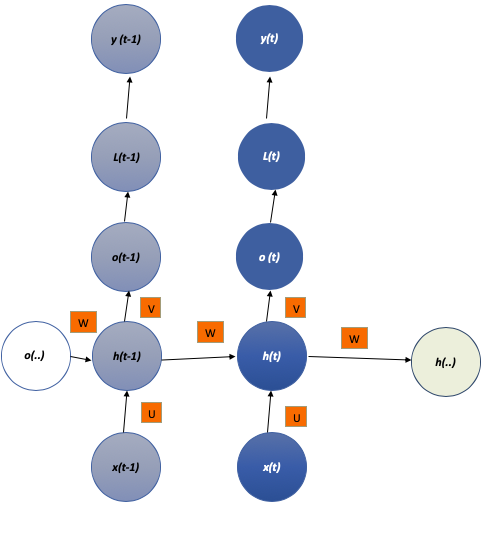
Чтобы рассчитать погрешность при обучении рекуррентной нейронной сети, потребуется вычислительный граф. Последовательность выходных значений o сравнивают с учебными (тренировочными) целями y. Так принимаем oза ненормализованные логарифмические вероятности. Функция потери L вычисляет внутри y^ = softmax(o) и сравнивает это с целевым значением y. У РНС есть вход в скрытые соединения. Они параметризованы весовыми матрицами U и W. А скрытое выходное подключение параметризовано матрицей весов V.

Каждый из трёх блоков ассоциируется с отдельной матрицей весов. Когда сеть развернута, каждый из этих блоков соответствует небольшой трансформации (она влияет на один слой).

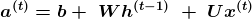
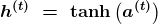
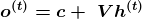
Уравнения вверху определяют последующее распространение этой модели. Оно начинается с определения начального состояния для каждого шага по времени от t = 1 до t= T.

Так выглядит РНС, которая отображает входную последовательность на выходную последовательность идентичной длины. Общая ошибка будет суммой ошибок за все время. L(t) является отрицательной логарифмической вероятностью y(t).

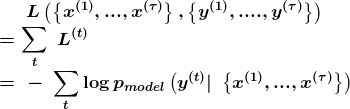
В вычисление градиента входит сдвиг последующего распространения слева направо. А дальше — метод обратного распространения ошибки проходит сдвиг справа налево. 

Состояния, вычисляемые в прямом распространении, должны быть использованы в обратном распространении. Их стоит сохранить. Алгоритм обратного распространения, применяемый при помощи выводной функции o(t),называется “обратное распространение на отрезке времени”. Вычисление градиента через рекуррентную нейронную сеть происходит четко вперёд. Он просто использует алгоритм обратного распространения, чтобы развернуть вычислительный граф. Градиенты, которые получают при помощи обратного распространения, можно использовать для тренировки РНС. 

Давайте сделаем модель РНС в Pytorch. Мы создаем псевдо-код здесь. Все части кода опубликованы по ссылке на мой GitHub: здесь. 

Обучение Pytorch MNIST

Для начала мы импортируем классы и набор данных MNIST.

import torch
import torchvision
import torch.nn as nn
import torchvision.transforms as transforms
import torchvision.datasets as dsets
import numpy as np
from matplotlib import pyplot as plt

n_epochs = 3
batch_size_train = 64
batch_size_test = 1000
learning_rate = 0.01
momentum = 0.5
log_interval = 10

random_seed = 1
torch.backends.cudnn.enabled = False
torch.manual_seed(random_seed)

train_loader = torch.utils.data.DataLoader(dsets.MNIST(‘/Users/akhileshrai/Downloads’, train=True, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])),
batch_size=batch_size_train, shuffle=True)

test_loader = torch.utils.data.DataLoader(
dsets.MNIST(‘/Users/akhileshrai/Downloads’, train=False, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])),
batch_size=batch_size_test, shuffle=True)

examples = enumerate(test_loader)
batch_idx, (example_data, example_targets) = next(examples)

import matplotlib.pyplot as plt

fig = plt.figure()
for i in range(6):
plt.subplot(2,3,i+1)
plt.tight_layout()
plt.imshow(example_data[i][0], cmap=’gray’, interpolation=’none’)
plt.title(“Number: {}”.format(example_targets[i]))
plt.xticks([])
plt.yticks([])
print(fig)

Команда data loaders загружает набор данных MNIST. Датасет помещается в упомянутую папку. Трансформации нужны для того, чтобы сначала конвертировать данные в тензоры, а затем нормализовать их.

Давайте посмотрим на то же самое при печати сэмплов тестового набора данных.

Давайте подготовим нашу нейросеть на базе показанной выше архитектуры:

class RNNModel(nn.Module):
def __init__(self, input_dim, hidden_dim, layer_dim, output_dim):
super(RNNModel, self).__init__()
# Скрытые признаки
self.hidden_dim = hidden_dim

# Количество скрытых слоёв
self.layer_dim = layer_dim

# Строим нейросеть
# batch_first=True causes input/output tensors to be of shape
# (batch_dim, seq_dim, input_dim)
# batch_dim = number of samples per batch
self.rnn = nn.RNN(input_dim, hidden_dim, layer_dim, batch_first=True, nonlinearity=’tanh’)

# Слой чтения вывода
self.fc = nn.Linear(hidden_dim, output_dim)

def forward(self, x):
# Инициализация скрытого состояния нулями.
# (layer_dim, batch_size, hidden_dim)
h0 = torch.zeros(self.layer_dim, x.size(0), self.hidden_dim).requires_grad_()

# Нам нужно отсоединить скрытое состояние, чтобы предотвратить градиентный взрыв и вымывание градиента.

# This is part of truncated backpropagation through time (BPTT)
out, hn = self.rnn(x, h0.detach())

# Индекс скрытого состояния последнего временного шага
# out.size() → 100, 28, 10
# out[:, -1, :] → 100, 10 → последний шаг скрытого состояния.
out = self.fc(out[:, -1, :])
# out.size() → 100, 10
return out

input_dim = 28
hidden_dim = 100
layer_dim = 3
output_dim = 10

model = RNNModel(input_dim, hidden_dim, layer_dim, output_dim)

print(model)
print(len(list(model.parameters())))
for i in range(len(list(model.parameters()))):
print(list(model.parameters())[i].size())

В нашей модели есть 3 скрытых слоя и по 100 скрытых нейронов на каждом из них. Она принимает входящие данные по 28 измерениям, а возвращает десятимерные данные. 

Функция активации, которую мы присвоили, — это “гиперболический тангенс”. Стохастический градиентный спуск нужен для того, чтобы найти градиент функции стоимости единичного примера в каждой итерации вместо суммы градиента функции стоимости всех примеров.

Дальше модель проходит 5000 итераций обучения, а метод ранней остановки нужен для того, чтобы модель не переобучилась. 

Ранняя остановка — это техника оптимизации, которая реализована путем вычисления потери (ошибки) валидации. Если отклонение валидации не падает ниже определенного количества итераций, то модель останавливает свое обучение. 

learning_rate = 0.01
min_val_loss = np.Inf
epochs_no_improve = 0
n_epochs_stop = 2
early_stop = False

optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
# Количество откатываемых шагов
criterion = nn.CrossEntropyLoss()

# Количество откатываемых шагов
seq_dim = 28
early_stop = False
iter = 0
for epoch in range(num_epochs):

val_loss = 0
for i, (images, labels) in enumerate(train_loader):
# Загрузить изображения в качестве тензор torch с возможностью аккумуляции градиента
images = images.view(-1, seq_dim, input_dim).requires_grad_()

# Чёткие градиенты по параметрам
optimizer.zero_grad()

# Следующая передача для получения выходных данных/логитов
# outputs.size() → 100, 10
outputs = model(images)

# Вычисление ошибки: softmax → ошибка перекрестной энтропии
loss = criterion(outputs, labels)

# Получение градиентов по параметрам
loss.backward()

# Обновление параметров
optimizer.step()

val_loss += loss
val_loss = val_loss / len(train_loader)
# Если по оценке ошибка минимальная
if val_loss < min_val_loss:
# Сохранение модели
#torch.save(model)
epochs_no_improve = 0
min_val_loss = val_loss

else:
epochs_no_improve += 1
iter += 1

if iter % 500 == 0:
# Расчёт точности
correct = 0
total = 0
# Итерация с учебным датасетом
# Проверка условия ранней остановки 
if epochs_no_improve == n_epochs_stop:
print('Early stopping!')
early_stop = True
break
else:
continue
break
if early_stop:
print("Stopped")
break

Для изображений, меток в test_loader.

# Изменение размеров изображений
images = images.view(-1, seq_dim, input_dim)

# Следующий прогон только для получения логитов и выходных данных
outputs = model(images)

# Получение прогнозов из максимального значения
_, predicted = torch.max(outputs.data, 1)

# Общее число меток
total += labels.size(0)

# Общие точные прогнозы
correct += (predicted == labels).sum()

accuracy = 100 * correct / total

# Вывод ошибки
print('Iteration: {}. Loss: {}. Accuracy: {}'.format(iter, loss.item(), accuracy))

Исследование модели и заключение:

Модель показала себя хорошо, потому что обнаружила введенные вручную цифры, которые не коррелировались с предшествующими. Если бы цифры коррелировались между последовательностей (и в долгом, и в быстром вариантах), то модель показала бы себя не очень результативно. 

Алгоритм обратного распространения ошибки во времени дорогой из-за состояний, которые вычисляются в прямом прогоне и будут сохранять их до тех пор, пока они переиспользуются в обратном прогоне. Так что тут еще и стоимость памяти O(T).

Еще одна проблема, с которой сталкиваются РНС — это “обрывы”. Они случаются с нелинейными функциями, потому что у них есть тенденция с производными —  они могут быть слишком большими или наоборот, слишком маленькими по размеру. Чтобы получить уменьшение градиента более разумно и ограничить размер шага, применяется техника “отсечение градиентов”.

Надеюсь, эта информация помогла вам понять, как устроены РНС и как их развитие формирует мир глубокого обучения.

Читайте также:

• Нейронная сеть с нуля при помощи numpy
• Пишем нейронную сеть, предсказывающую рак груди, за пять минут
• Как выбрать модель машинного обучения

---

Перевод статьи Akhilesh Rai: Recurrent Neural Network-Head to Toe