1. Восприятие условной независимости
Скажем, A — рост ребенка, а B — количество слов, которые он знает. Кажется, что если A высокий, то B, соответственно, тоже.
Однако существует информация, которая делает A и B совершенно независимыми друг от друга. Что бы это могло быть?
Возраст ребенка.
Рост и количество известных ребенку слов НЕ являются независимыми, но они становятся условно независимыми, если вы добавите параметр возраста.
2. Математическая форма

A: Рост ребенка
B: Количество известных ребенку слов
C: Возраст ребенка
Лучший способ запомнить выражение:

Условная независимость — это основная концепция независимости P(A ∩ B) = P(A) * P(B), применяемая в условной модели.
Но я видела не только такое определение, как P(A ∩ B|C), но и P(A|B ∩ C).

Почему P(A|B ∩ C) = P(A|C), когда (Aㅛ B)|C?
Вот доказательство.
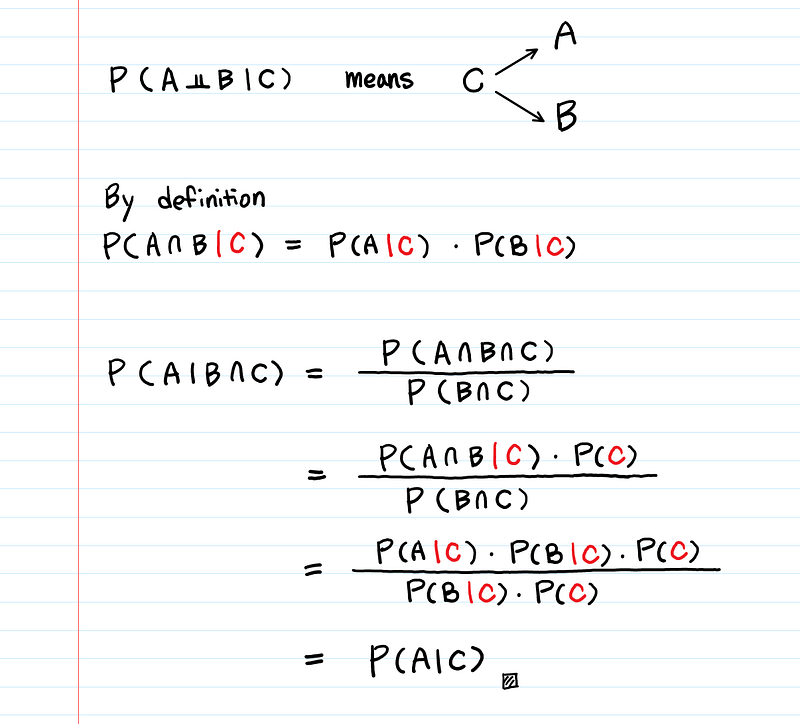
Суть условной независимости: если мы знаем C, то A и B независимы друг от друга.
P(A,B|C) = P(A|C) * P(B|C)
3. Применение?
Почему условная независимость важна?
Потому что она лежит в основе многих статистических моделей, которые мы используем (например, латентной модели, факторного анализа, графовых моделей т.д.).
A. Условная независимость в байесовской сети (графовые модели)
Байесовская сеть представляет совместное распределение с использованием направленного ациклического графа, в котором каждое ребро является условной зависимостью, а каждый узел — отдельной случайной величиной. Существует множество других названий: сеть доверия, сеть решений, причинная сеть, Байесова модель, вероятностная направленная ациклическая графическая модель и т.д.
Выглядит это так:
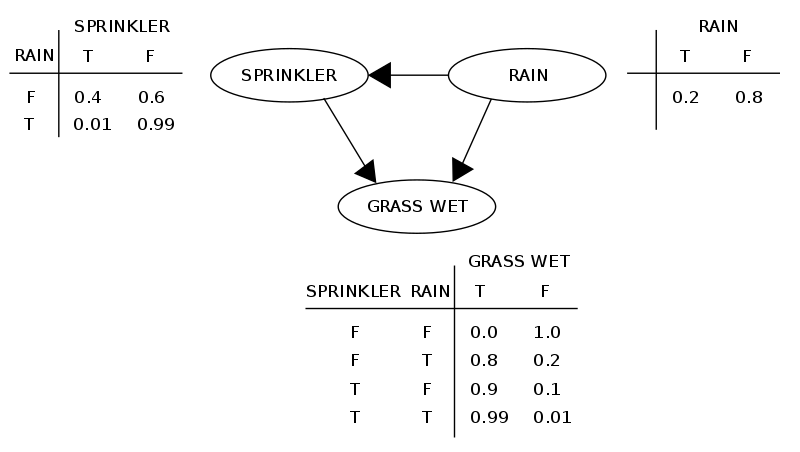
Чтобы байесовская сеть моделировала распределение вероятностей, она опирается на важное условие: каждая переменная условно независима от своих не-потомков, включая родителей.
К примеру, мы можем упростить P(Мокрая трава|Дождевальная установка, Дождь) до P(Мокрая трава|Дождевальная установка), поскольку Мокрая трава условно не зависит от своего не-потомка, Дождя, влияющего также на Дождевальную установку.
Используя это свойство, мы можем упростить совместное распределение в формулу ниже:

Что такого прекрасного в этой аппроксимации (свойстве условной независимости)?
Условная независимость между переменными может значительно уменьшить количество параметров
Это сильно сокращает объём вычислений, ведь теперь нам нужно считать только родительский элемент, остальное можно проигнорировать.
Давайте посмотрим на числа.
Скажем, у вас есть n двоичных переменных (= n ребер).
Неограниченное совместное распределение требует O(2^n) вероятностей.
Для байесовской сети с максимумом k родителей для каждого узла нам нужна только O(n * 2^k) вероятностей (что может быть выполнено в линейное время для определенного числа классов).
n = 30 двоичных переменных, k = 4 максимальное число родителей для узла • Неограниченное совместное распределение: нужно 2^30 (около 1 миллиона) вероятностей -> Трудно обрабатывать! • Байесовская сеть: нужно только 480 вероятностей
С использованием условной независимости мы можем получить эффективное факторизованное представление для совместного распределения.
B. Условная независимость в байесовском выводе
Скажем, я хочу оценить уровень вовлеченности (лайки) читателей моего блога. Пусть p будет пропорцией читателей, поставивших лайк моим статьям. Выбираем n читателей случайным образом. Для i = 1, …, n, пусть Xi = 1 если читатель поставил лайк и Xi = 0, если нет.
В частотно-вероятностном подходе нам не нужно определять распределение p. Онопросто будет равно ‘sum (Xi) / n’. И мы рассматриваем X1, …, Xn как независимые случайные переменные.
С другой стороны, в байесовском выводе мы предполагаем, что p не является постоянной, а зависит от распределения. В этой модели случайные переменные X1, …, Xn не являются независимыми, но они условно независимы, учитывая распределение p.
C. Корреляция не есть причинная связь
То есть, если две вещи коррелируют, это не обязательно значит, что одна является причиной другой.
Вот забавный пример про аварии с участием такси:
Исследование показало положительную и значительную корреляцию между количеством инцидентов и тем, что водители носили куртки. Исследователи предположили, что куртка может сковывать движения водителя и провоцировать аварии. Уже готов был новый закон, запрещающий водителям такси носить их.
Пока другое исследование не показало, что люди носят куртки и во время дождя… ?
P(аварии, куртки | дождь) = P(аварии | дождь) * P(куртки | дождь)
Корреляция между двумя событиями может быть спровоцирована третьим фактором, влияющим на оба эти события. Этот третий фактор называется вмешивающимся фактором. В нашем примере дождь — вмешивающийся фактор, он ответственен за корреляцию между количеством аварий и ношением курток.
P(аварии | куртки, дождь) = P(аварии | куртки)
Заметьте, что это НЕ означает, что аварии не зависят от дождя. Это означает следующее: если водитель носит куртку, то информация о том, идет ли дождь, нам ничего не даст.
4. Условная независимость в сравнении с обычной
Иногда две случайные переменные не могут быть просто независимыми. Но они могут стать таковыми после того, как мы обнаружим третью переменную.
5. Еще примеры!
- Уровень превышения скорости ㅛ Тип машины| Скорость
- Рак легких ㅛ Желтые зубы | Курение
- Гены детей ㅛ Гены внуков| Родительские гены
- Работает ли в машине стартер? ㅛ Работает ли в машине радио?| Аккумулятор
- Будущее ㅛ Прошлое| Настоящее (это Марковское свойство!)
Все они соответствуют форме A ㅛ B | C.
A и B выглядят взаимосвязанными, если мы не берем в расчет C. Однако, как только мы добавляем C, связь между A и B исчезает. Как вы видите, любые причинно-следственные связи потенциально условно независимы. Мы никогда достоверно не знаем о связи между A и B, пока не проверим все возможные C (вмешивающиеся переменные)!
Читайте также:
- Биномиальное распределение
- Значение Data Science в современном мире
- Шесть рекомендаций для начинающих специалистов по Data Science
Перевод статьи Aerin Kim: Conditional Independence — The Backbone of Bayesian Networks






