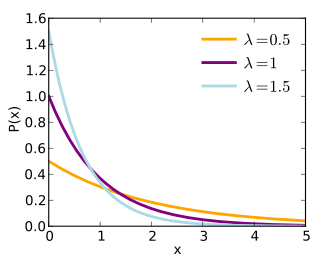
Мы всегда начинаем с вопроса “почему”, прежде чем переходить к формулам. Если вы понимаете, почему что-то работает, вы с большей вероятностью будете применять это в своей работе.
1. Почему мы изобрели экспоненциальное распределение?
Ответ: чтобы получить распределение, предсказывающее периоды времени между событиями (такими как успех, отказ, доставка и так далее).
Например, мы хотим предсказать следующее:
- Время, по истечении которого клиент закончит поиск и закажет что-то в магазине (успех).
- Время, по истечении которого оборудование AWS EC2 выйдет из строя (отказ).
- Время ожидания автобуса (прибытие).
Следующий вопрос такой: почему λ * e^(−λt) — это плотность вероятности времени до следующего события?
И следующий вопрос: что значит X~EXP(0,25)?Параметр 0,25 означает 0,25 минут, часов или дней, а, может, 0,25 событий?
Предполагается, что вы хорошо знакомы с распределением Пуассона. Если нет, эта статья поможет разобраться.
X~EXP(λ) ➡ Экспоненциальный параметр λ тот же самый, что и λ в распределении Пуассона?
Важная вещь, которая позже поможет вам не запутаться с X~EXP(0,25).0,25 — это не временной период, а число событий, совпадающее с параметром λ в процессе Пуассона.
Например, ваш блог посещают 500 пользователей в день. Это среднее значение. Количество клиентов магазина за час, землетрясений в год, автомобильных аварий в неделю, опечаток на странице и так далее — это средние значения событий (λ) в единицу времени, являющиеся параметром распределения Пуассона.
Однако при моделировании времени между событиями удобнее использовать термины времени, а не количества. Например, число лет, в течение которых компьютер может включаться без ошибок — 10 лет (это удобнее, чем говорить “0,1 ошибка в год”), новый покупатель приходит каждые 10 минут, крупные ураганы возникают каждые 7 лет и так далее.
Путаница возникает, когда вы видите термин “затухание”, или еще хуже, “скорость затухания”, которые часто используются в экспоненциальном распределении. Затуханиевыражается через время (каждые 10 минут, каждые 7 лет и т.д.) и является обратной величиной параметра (λ) в распределении Пуассона. Смотрите: если у вас 3 посетителя в час, значит у вас 1 посетитель каждую треть часа.
Итак, мы можем ответить на вопрос:
Что значит “X ~ EXP(0,25)”?
Это означает, что параметр Пуассона будет равен 0,25. В течение единицы времени (неважно, в минутах, часах или годах) событие происходит в среднем 0,25 раз. Переводя в термины времени — пройдет 4 часа, прежде чем событие произойдет, если за единицу времени принят 1 час.
* Чтобы не запутаться: параметр экспоненциального распределения λ тот же самый, что в процессе Пуассона (λ).
2. Вывод плотности вероятности
Наш первый вопрос был: почему λ * e^(−λt) — это плотность вероятности времени до следующего события?
Определение экспоненциального распределения — это распределение вероятности времени *между* событиями в процессе Пуассона.
Смотрите: в период ожидания не происходит ни одного события. Другими словами, Пуассон (X=0).
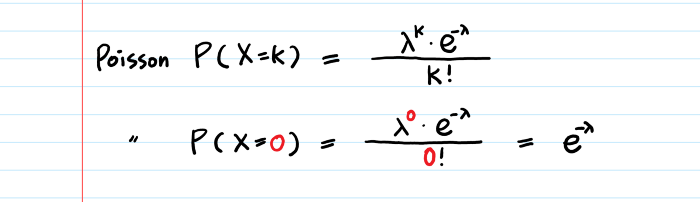
Есть важная вещь, которую стоит помнить о пуассоновской плотности вероятности: период времени, в течение которого возникают пуассоновские события (X=k), составляет только одну (1) единицу времени.
Как смоделировать распределение вероятности не просто в течение одной единицы времени, а “ничего не произошло в период времени t”?
P(ничего не произошло в течение t единиц времени)
= P(X=0 в первую единицу времени)
* P(X=0 во вторую единицу времени)
* … * P (X=0 в t-ую единицу времени)
= e^−λ * e^−λ * … * e^−λ = e^(-λt)
Распределение Пуассона предполагает, что события возникают независимо друг от друга. Следовательно, можно посчитать вероятность нулевого успеха в течение t единиц времени, умножив P(X=0 в единицу времени) на t раз.
P(T > t) = P(X=0 в t единиц времени) = e^−λt * T : случайная переменная времени до первого успешного события * X : количество событий * P(T > t) : вероятность того, что время ожидания события больше,чем t единиц времени * P(X=0 в t единиц времени): вероятность нулевого успеха в t единиц времени
Плотность вероятности — это производная от кумулятивной функции распределения вероятности.
Поскольку у нас уже есть кумулятивная функция распределения вероятности экспоненциального распределения, 1 — P(T > t), мы можем получить плотность вероятности, продифференцировав ее.
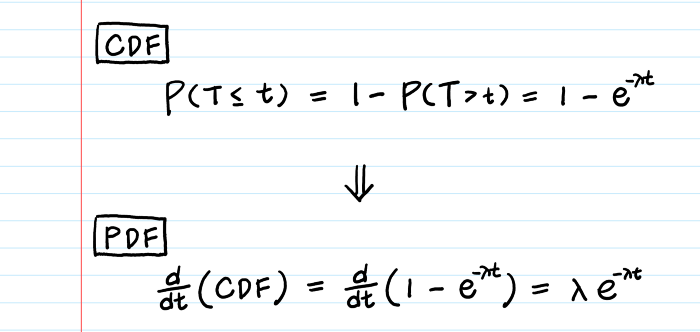
3. Отсутствие последействия
Определение: P(X > a + b | X > a) = P(X > b)
Это означает:
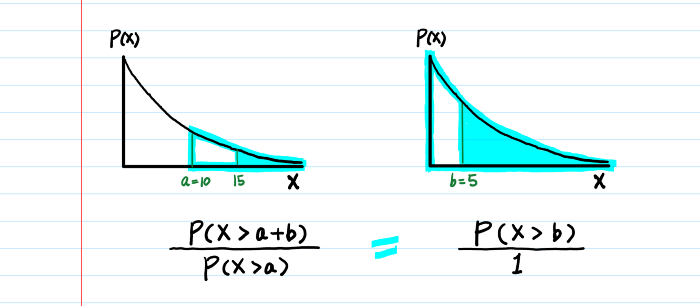
Доказательство:
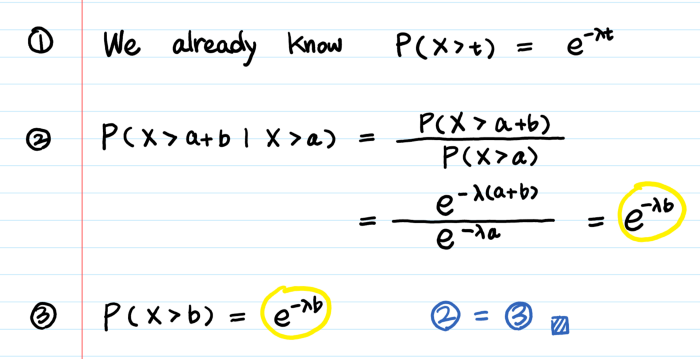
Отсутствие последействия — полезный параметр?
Рационально ли моделировать долговечность механического устройства, используя экспоненциальное распределение?
Например, если устройство уже проработало девять лет, отсутствие последействия означает, что вероятность его бесперебойной работы в следующие три года (то есть в сумме 12 лет) точно такая же, как для совершенно нового механизма.
P(X > 12|X > 9) = P(X > 3)
Это уравнение кажется вам разумным?
Мне нет. Как показывает мой опыт, чем старше устройство, тем вероятнее поломка. Смоделировать этот параметр — возрастающую интенсивность отказов — можно с помощью распределения Вейбулла.
Так когда же стоит применять экспоненциальное распределение (постоянную интенсивность отказов)?
Автомобильные происшествия. Если никто не врезался в вас за последние пять часов, это не снижает и не повышает шансы попадания в аварию.
Где еще есть отсутствие последействия?
Экспоненциальное распределение — это единственное непрерывное распределение с отсутствием последействия (или распределение с постоянной интенсивностью отказов). Геометрическое распределение, его дискретный аналог, является единственным дискретным распределением с отсутствием последействия.
4. Применение в реальной жизни ?
a) Моделирование времени ожидания
У значений экспоненциальной случайной величины есть много маленьких значений и немного крупных значений. Автобус, который вы ждете, скорее всего приедет в течение 10 минут нежели в течение 60 минут.
Используя экспоненциальное распределение, можно ответить на следующие вопросы:
1. Автобус в среднем приезжает каждые 15 минут (предположим, что время между прибытием автобусов имеет экспоненциальное распределение, значит, количество автобусов, прибывающих в течение часа имеет распределение Пуассона). И я только что пропустила автобус! Водитель был злой. Как только я пришла, он закрыл двери и уехал. Если следующий автобус не приедет в течение десяти мнут, я вызову Uber, иначе опоздаю. Какова вероятность того, что ожидание следующего автобуса займет меньше 10 минут?
2. Девяносто процентов автобусов прибывают через сколько минут после предыдущего?
3. В течение какого времени в среднем прибывают два автобуса?
b) Моделирование отказа
Раз мы можем смоделировать успешное событие (прибытие автобуса), почему бы не смоделировать отказ — время поломки продукта.
Количество часов, которое AWS оборудование способно проработать без перезагрузки, соответствует экспоненциальному распределению со средним значением 8 000 часов в год.
1. У вас нет резервного сервера, а вам нужна бесперебойная работа в течение 10 000 часов. Какова вероятность того, что вы сможете выполнить эту задачу без перезагрузки сервера?
2. Какова вероятность того, что сервер не потребует перезагрузки между 12 и 18 месяцами?
Заметьте, что иногда экспоненциальное распределение не подходит — когда интенсивность отказов изменяется в течение срока службы. Тем не менее это единственное распределение, обладающее уникальным параметром — постоянной интенсивностью отказов.
c) Моделирование времени обслуживания (Теория очередей)
Время обслуживания (например, как долго в кафе готовят мне буррито) тоже можно смоделировать как экспоненциально распределенные переменные.
Общая длина процесса — последовательность нескольких независимых задач — соответствует распределению Эрланга: распределению суммы нескольких независимых экспоненциально распределенных переменных.
5. Вкратце: связь между экспоненциальным и пуассоновским распределениями
Если число событий в единицу времени соответствует распределению Пуассона, тогда период времени между событиями соответствует экспоненциальному распределению.
Предположим, что на период времени между событиями не влияют предыдущие события (то есть они независимы), тогда число событий в единицу времени соответствует распределению Пуассона со значением λ = 1/μ.
6. Упражнение
Как оказалось, в понимании математических тем мне помогает решение задач. Попробуйте решить задания ниже.
- Пусть U — случайная величина, имеющая равномерное распределение между 0 и 1. Тогда экспоненциальная случайная переменная будет выглядеть так
X = -1/λ * ln(U)
Докажите почему.
2. Максимальное значение плотности распределения вероятности на оси y — λ. Почему?
3. X1 и X2 — независимые экспоненциальные случайные переменные со значением λ.
X1~EXP(λ)
X2~EXP(λ)
Пусть Y=X1+X2.
Какова плотность вероятности Y?
Где может быть использовано это распределение?
Читайте также:
- Биномиальное распределение
- Что такое распределение Пуассона?
- Плотность вероятности - это не сама вероятность
Перевод статьи Aerin Kim: Exponential Distribution Intuition, Derivation and Applications