Выборки. Джентльменский набор

Простая случайная выборка

Вы хотите выбрать подмножество, в котором каждый член имеет равную вероятность быть выбранным. Ниже мы случайно выбираем 100 значений из набора данных:

sample_df = df.sample(100)

Название говорит само за себя. Это всё.

Стратифицированная выборка

Нам нужно оценить среднее количество голосов для каждого кандидата на выборах. В стране есть 3 города:

• Город A с миллионом рабочих на фабрике.
• Город B с 2 миллионами рабочих.
• Город C с 3 миллионами пенсионеров.

Мы можем выбрать случайную выборку в 60 человек во всех городах, но есть некоторый шанс, что она окажется недостаточно сбалансированной по всем городам. Следовательно, она будет смещена, что приведет к значительной ошибке в оценке.

Если мы вместо этого сделаем случайную выборку 10, 20 и 30 человек из городов A, B и C, то можем получить меньшую ошибку в оценке для того же общего размера выборки. Сделать это в Python легко:

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y,
                                                    stratify=y, 
                                                    test_size=0.25)

Резервуарная выборка

Люблю эту задачу: у нас есть поток элементов большой и неизвестной длины, который можно прочитать только один раз. Создайте алгоритм, случайным образом выбирающий элемент из этого потока так, что каждый элемент будет выбран с равной вероятностью. Как это можно сделать? Предположим, у нас k = 5 элементов:

import randomdef generator(max):
    number = 1
    while number < max:
        number += 1
        yield number # Создаём генератор.
stream = generator(10000) # Делаем выборку.
reservoir = []
for i, element in enumerate(stream):
    if i+1<= k:
        reservoir.append(element)
    else:
        probability = k/(i+1)
        if random.random() < probability:
            # Выбираем новый элемент. Удаляем один из уже выбранных.
             reservoir[random.choice(range(0,k))] = elementprint(reservoir)
------------------------------------
[1369, 4108, 9986, 828, 5589]

Правильность алгоритма можно доказать математически. Как? Подумайте о еще меньшем количестве элементов. В математике это всегда помогает. 

Допустим, в потоке всего 3 элемента, а 2 в резервуаре. Мы видим первый элемент, оставляем его в списке, так как в нашем резервуаре достаточно места. Мы видим второй элемент и поступаем так же по той же причине. Видим третий элемент. Здесь становится интересно! Выбираем третий элемент с вероятностью 2/3. 

Посмотрим на вероятность выбора первого элемента:

Вероятность удаления первого элемента  —  это вероятность выбора элемента 3, умноженная на вероятность случайного выбора элемента 1 в качестве кандидата на замену из двух элементов в резервуаре, 2/3*1/2 = 1/3. Значит, вероятность его выбора: 1 – 1/3 = 2/3. То же и для второго элемента, а значит, закономерность расширяется на любой диапазон. Каждый элемент выбирается с вероятностью k/n.

Случайное удаление/добавление экземпляров

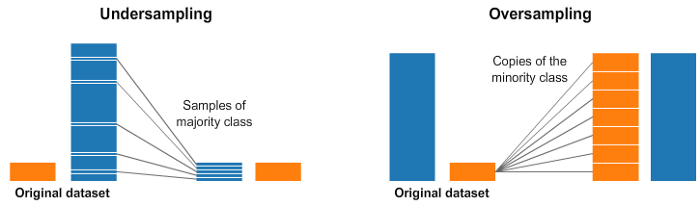
Обычно мы сталкиваемся с этим в несбалансированном наборе данных. Широко распространённый метод работы с сильно несбалансированными наборами  —  повторная выборка. Он состоит в удалении выборок из класса большинства (сужение, undersampling) и/или добавления большего количества примеров из класса меньшинства  —  дублирование элементов, oversampling. 

Создадим пример несбалансированных данных:

from sklearn.datasets import make_classificationX, y = make_classification(
    n_classes=2, class_sep=1.5, weights=[0.9, 0.1],
    n_informative=3, n_redundant=1, flip_y=0,
    n_features=20, n_clusters_per_class=1,
    n_samples=100, random_state=10
)X = pd.DataFrame(X)
X['target'] = y

Сейчас мы можем сделать случайное удаление или дублирование элементов:

num_0 = len(X[X['target']==0])
num_1 = len(X[X['target']==1])
print(num_0,num_1)
# random undersample
undersampled_data = pd.concat([ X[X['target']==0].sample(num_1) , X[X['target']==1] ])
print(len(undersampled_data))
# random oversample
oversampled_data = pd.concat([ X[X['target']==0], X[X['target']==1].sample(num_0, replace=True) ])
print(len(oversampled_data))
------------------------------------------------------------
OUTPUT:
90 10
20
180

Under/oversampling в несбалансированных наборах

imblearn  —  модуль Python, созданный специально для наборов с дисбалансом. Он предоставляет методы расширения и сужения выборок.

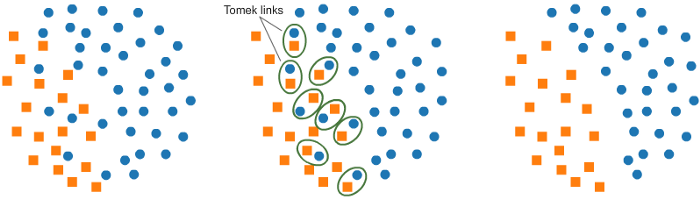
1. Связи Томека

Один из таких методов  —  поиск связей Томека. Он состоит в поиске элементов противоположного класса на близком расстоянии. Это обеспечивает более точную классификацию.

from imblearn.under_sampling import TomekLinks

tl = TomekLinks(return_indices=True, ratio='majority')
X_tl, y_tl, id_tl = tl.fit_sample(X, y)

2. Генерация искусственных элементов

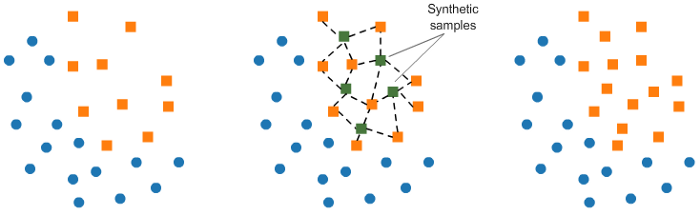
SMOTE (Synthetic Minority Oversampling Technique) искусственно создаёт примеры меньшего класса данных без дублирования.

from imblearn.over_sampling import SMOTE

smote = SMOTE(ratio='minority')
X_sm, y_sm = smote.fit_sample(X, y)

В imblearn есть и другие методы решения этих задач.

Заключение

Алгоритмы  —  это кровь науки о данных, но мы редко напоминаем себе об этом. У вас хорошая стратегия выборки  —  проект идет вверх. Плохая стратегия  —  и он провален. Будьте внимательны при выборе алгоритма.

Проект на Kaggle

Читайте также:

• Шесть рекомендаций для начинающих специалистов по Data Science(Opens in a new browser tab)
• Что такое распределение Пуассона?
• Руководство по машинному обучению для новичков

---

Перевод статьи Rahul Agarwal: The 5 Sampling Algorithms every Data Scientist need to know