
Деревья решений являются классом очень эффективной модели машинного обучения, позволяющей получить высокую точность в решении многих задач, сохраняя при этом высокий уровень интерпретации. Четкость представления информации делает деревья решений особенными среди других моделей машинного обучения. Освоенные деревом решений «знания» напрямую формируются в иерархическую структуру, которая хранит и представляет знания в понятном даже для неспециалистов виде.

Деревья решений в реальной жизни
Вы скорее всего уже использовали деревья решений для того, чтобы сделать какой-нибудь выбор в своей жизни. Например, нужно решить, чем вы займетесь на предстоящих выходных. Итог может зависеть от того, хотите ли вы пойти куда-то с друзьями или провести выходные в одиночестве. В обоих случаях решение зависит также и от погоды. Если она будет солнечной и друзья будут свободны, вы можете сходить поиграть в футбол. Если пойдет дождь, вы пойдете в кино. Если друзья будут заняты, то вы останетесь дома играть в видео игры, даже несмотря на хорошую погоду.
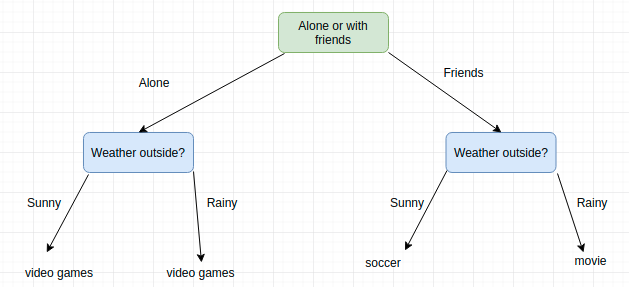
Этот пример хорошо демонстрирует дерево решений в реальной жизни. Мы построили дерево и смоделировали ряд последовательных, иерархических решений, которые, в конечном итоге, приводят к некоторому результату. Обратите внимание, что мы выбрали максимально общие варианты решения, чтобы дерево было маленьким. Дерево будет просто огромным, если мы установить многовозможных вариантов погоды, например: 25 градусов, солнечно; 25 градусов, дождливо; 26 градусов, солнечно; 26 градусов, дождливо; 27 градусов, солнечно; 27 градусов, дождливо и т.д. Конкретнаятемпература не важна. Нам нужно лишь знать, будет ли погода хорошей или нет.
В машинном обучении концепция деревьев решений такая же. Нам нужно построить дерево с набором иерархических решений, которые в конце приведут нас к результату, то есть к нашей классификации или прогнозу регрессии. Решения выбираются таким образом, чтобы дерево было максимально маленьким, но при этом сохраняло точность классификации или регрессии.
Деревья решений в машинном обучении
Модели дерева решений строятся в два этапа: индукция и отсечение. Индукция — это то, где мы строим дерево, то есть устанавливаем все границы иерархического решения, основываясь на наших данных. Из-за своего характера обучаемые деревья решений могут быть подвержены значительному переобучению. Отсечение — это процесс удаления ненужной структуры из дерева решений, эффективно упрощая его для понимания и избежания переобучения.
Индукция
Индукция дерева решений проходит 4 главных этапа построения:
- Начните с обучающего набора данных, в котором должны содержаться признаки переменных и результаты классификации или регрессии.
- Определите «лучший признак » в наборе данных для их разбиения. О том, как определить этот «лучший признак » поговорим позже.
- Разбейте данные на подмножества, которые будут содержать возможные значения для лучшего признака. Такое разбиение в основном определяет узел на дереве, то есть каждый узел — это разделенная точка, основанная на определенном признаке из наших данных.
- Рекурсивно сгенерируйте новые узлы дерева с помощью подмножества данных, созданных на 3 этапе. Продолжайте разбиение до тех пор, пока не достигните точки, на которой будет находится оптимизированная каким-то способом максимальная точность. Старайтесь минимизировать количество разбиений и узлов.
Первый этап простой. Просто соберите свой набор данных!
На втором этапе выбор признака и определенного разбиения обычно осуществляется с помощью жадного алгоритма для уменьшения функции стоимости. Если подумать, разбиение при построении дерева решений эквивалентно разбиению признакового пространства. Мы будем несколько раз пробовать разные точки разбиения, а в конце выберем ту, которая имеет наименьшую стоимость. Конечно, можно проделать пару умных вещей, таких как разбиение только в диапазоне значений в нашем наборе данных. Это позволит сократить количество вычислений для тестирования точек разбиений, которые являются заведомо бесполезными.
Для дерева регрессии можно использовать простой квадрат ошибки в качестве функции стоимости:
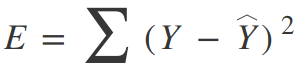
Где Y — это достоверные данные, а Y с шапкой — это прогнозируемое значение. Мы суммируем по всем выборкам в нашем наборе данных, чтобы получить общую ошибку. Для классификации мы используем функцию коэффициента Джини:
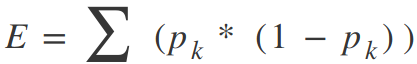
Где pk — это доля обучающих примеров класса k в определенном узле прогнозирования. В идеале узел должен иметь значение ошибки, равное нулю, означающее, что каждое разбиение выводит один класс 100% времени. Это именно то, что нам нужно, так как добравшись до конкретно этого узла принятия решения, мы будем знать, каким будет вывод в зависимости от того, на какой стороне границы мы находимся.
Такая концепция единственного класса на узел в наборе данных называется «прирост информации». Посмотрите на пример ниже.
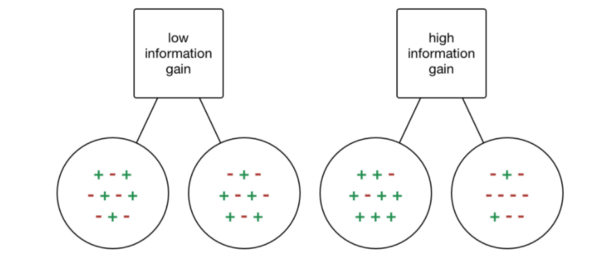
Если бы нам пришлось выбрать разбиение, на котором каждый выход имеет разные классы в зависимости от входных данных, тогда бы мы не добыли никакой информации. Мы не узнали бы больше о том, влияет ли конкретный узел, то есть функция, на классификацию данных! С другой стороны, если наше разбиение имеет высокий процент каждого класса для каждого выхода, то мы добылиинформацию о том, что разбиение таким конкретным образом на эту конкретную переменную дает нам конкретный выход!
Теперь мы могли бы продолжить разбиение до тех пор, пока у нашего дерева не появятся тысячи ветвей… Но это плохая идея! Наше дерево решений было бы огромным, медленным и переобученным для нашего обучающего набора данных. Поэтому мы установим некоторые заранее определенные критерии остановки, чтобы прекратить построение дерева.
Наиболее распространенным методом остановки является использование минимального расчета по количеству обучающих примеров, назначенных для каждой вершины дерева. Если число меньше некоторого минимального значения, то разбиение не считается и узел назначается конечной вершиной дерева. Если все вершины дерева становятся конечными, то обучение прекращается. Чем меньше минимальное число, тем точнее будет разбиение и, соответственно, вы получите больше информации. Но в таком случае минимальное число склонно к переобучению обучающими данными. Слишком большое количество минимальных чисел приведет к остановке обучения слишком рано. Таким образом, минимальное значение обычно устанавливается на основе данных в зависимости от того, сколько примеров ожидается в каждом классе.
Отсечение
Из-за своего характера обучающие деревья решений могут быть подвержены значительному переобучению. Выбор правильного значения для минимального количества примеров на узел может оказаться сложной задачей. Во многих случаях можно было бы просто пойти по безопасному пути и сделать этот минимум очень маленьким. Но в таком случае, у нас было бы огромное количество разбиений и, соответственно, сложное дерево. Дело в том, что многие из получившихся разбиений окажутся лишними и не помогут увеличить точность модели.
Отсечение ветвей дерева — это метод, сокращающий количество разбиений с помощью удаления, т.е. отсечения, ненужных разбиений дерева. Отсечение обобщает границы решений, эффективно уменьшая сложность дерева. Сложность дерева решений определяется количеством разбиений.
Простой, но очень эффективный метод отсечения происходит снизу вверх через узлы, оценивая необходимость удаления определенного узла. Если узел не влияет на результат, то он отсекается.
Пример в Scikit-learn
Деревья решений как для классификации, так и для регрессии удобно использовать в библиотеке Scikit-learn со встроенным классом! Сначала загружаем набор данных и инициализируем дерево решений для классификации. Провести обучение будет очень просто!
from sklearn.datasets import load_iris
from sklearn import tree
# Load in our dataset
iris_data = load_iris()
# Initialize our decision tree object
classification_tree = tree.DecisionTreeClassifier()
# Train our decision tree (tree induction + pruning)
classification_tree = classification_tree.fit(iris_data.data, iris_data.target)
Scikit-learn также позволяет визуализировать дерево с помощью библиотеки graphviz, в которой есть несколько очень полезных опций для визуализации узлов решений и разбиений, выученных моделью. Ниже обозначим узлы разными цветами, отталкиваясь от признаков имен, и отобразим класс и признак каждого узла.
import graphviz
dot_data = tree.export_graphviz(classification_tree, out_file=None,
feature_names=iris.feature_names,
class_names=iris.target_names,
filled=True, rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
graph.render("iris")
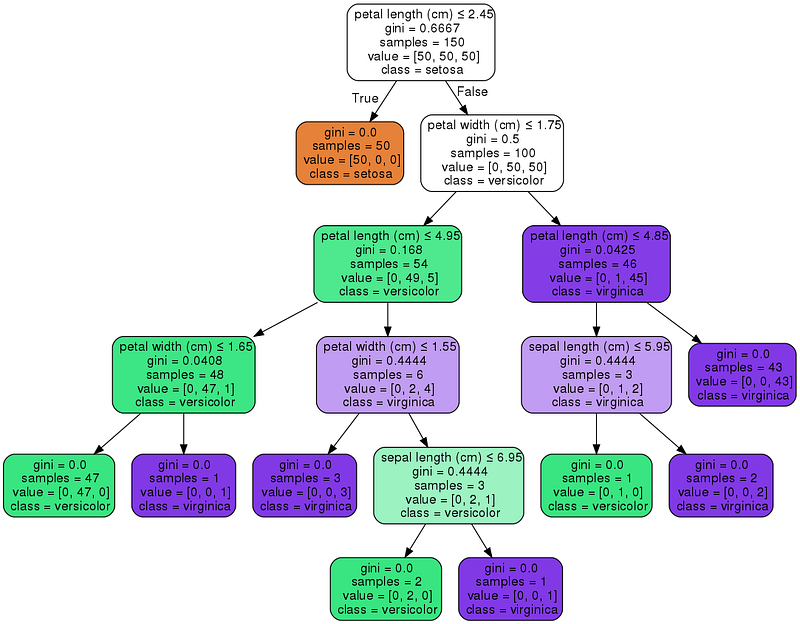
Кроме того, в Scikit-learn можно указать несколько параметров для модели дерева решений. Ниже приведем некоторые из таких параметров, позволяющих получить лучший результат:
- max_depth: максимальная глубина дерева — точка, на которой останавливается разбиение узлов. Это похоже на выбор максимального количества слоев в глубокой нейронной сети. Меньшее количество сделает модель быстрой, но не точной. Большее количество увеличивает точность, но создает риски переобучения и замедляет процесс.
- min_samples_split: необходимое минимальное количество выборок для разбиения узлов. Мы уже обсуждали это выше вместе с тем, как настроить высокое значение, чтобы минимизировать переобучение.
- max_features: число признаков для поиска лучшей точки для разбиения. Чем больше число, тем лучше результат. Но в этом случае обучение займет больше времени.
- min_impurity_split: порог для ранней остановки роста дерева. Узел разобьется только в том случае, если его точность будет выше указанного порога. Такой метод может служить в качестве компромисса между минимизацией переобучения (высокое значение, маленькое дерево) и высокой точностью (низкое значение, большое дерево).
- presort: выбор того, нужно ли предварительно сортировать данные для ускорения поиска наилучшего разбиения при подборе. Если данные заранее отсортируются по каждому признаку, то алгоритму обучения будет гораздо проще найти хорошие значения для разбиения.
Советы по практическому применению деревьев решений
Ниже опишем все плюсы и минусы деревьев решений, которые помогут вам понять, нужно ли строить такую модель для решения определенной задачи или нет. Также дадим некоторые советы о том, как их можно эффективно использовать.
Плюсы
- Их легко понять. В каждом узле мы можем точно увидеть, какое решение принимает наша модель. На практике мы сможем точно узнать, откуда исходят точности и ошибки, с какими видами данных модель будет справляться и как значения признаков влияют на выход. Опция визуализация в Scikit-learn является удобным инструментом, способствующим хорошему пониманию деревьев решений.
- Не требует объемной подготовки данных. Многие модели машинного обучения требуют предварительной обработки данных (например, нормализации) и нуждаются в сложных схемах регуляризации. С другой стороны, деревья решений эффективны после настройки некоторых параметров.
- Стоимость использования дерева для вывода является логарифмической от числа точек данных, используемых для обучения дерева. Это является большим преимуществом, так как большое количество данных не сильно повлияет на скорость вывода.
Минусы
- Из-за своего характера обучения деревья решений подвержены переобучению. Рекомендуется часто применять некоторые виды понижения размерности, например, PCA, чтобы дерево не создавало разбиения по большому количеству признаков.
- По тем же причинам, что и переобучение, деревья решений также уязвимы к смещению классов, которые есть в большинстве наборов данных. Хорошим решением в данном случае является периодическая балансировка классов (веса класса, выборка, определенная функция потерь).
Перевод статьи George Seif:A Guide to Decision Trees for Machine Learning and Data Science






