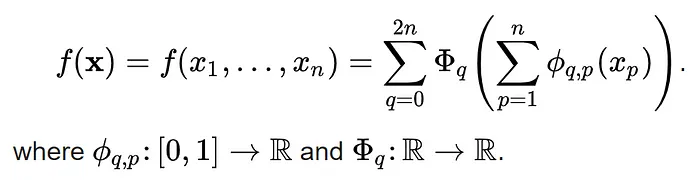Краеугольным камнем ИИ является MLP (multi-layer perceptron — многослойный перцептрон). Нейронная архитектура MLP определяет ландшафт бесчисленных приложений. Однако сети Колмогорова-Арнольда (KAN) стремятся разрушить этот традиционный фундамент, переосмыслив саму суть работы нейронов в нейронных сетях.
Введение
В постоянно развивающемся ландшафте машинного обучения недавняя исследовательская работа под названием “KAN: сеть Колмогорова-Арнольда” вызвала волну восторга среди энтузиастов. Этот инновационный подход бросает вызов общепринятым представлениям о MLP, предлагая новый взгляд на архитектуру нейронных сетей.
Что такое сеть Колмогорова-Арнольда?
В основе этой новаторской концепции лежит теорема представления Колмогорова-Арнольда — математическая теория, разработанная Владимиром Арнольдом и Андреем Колмогоровым. Эта теорема утверждает, что сложные многомерные функции могут быть разложены на более простые одномерные функции, закладывая основу для уникальной структуры KAN.
Что же это за “более простые одномерные функции”? Для тех, кто хоть немного знаком с математикой или вычислительной графикой, очевидно, что речь идет о старых и проверенных временем кусочно-заданных полиномах, известных как сплайны.
Сплайны как секретный ингредиент KAN
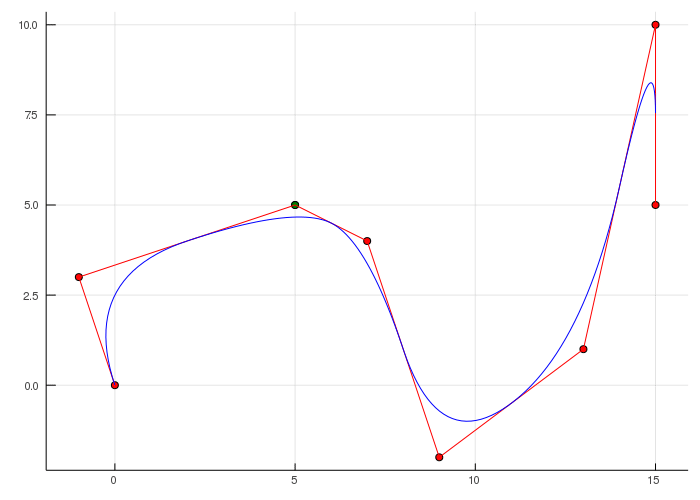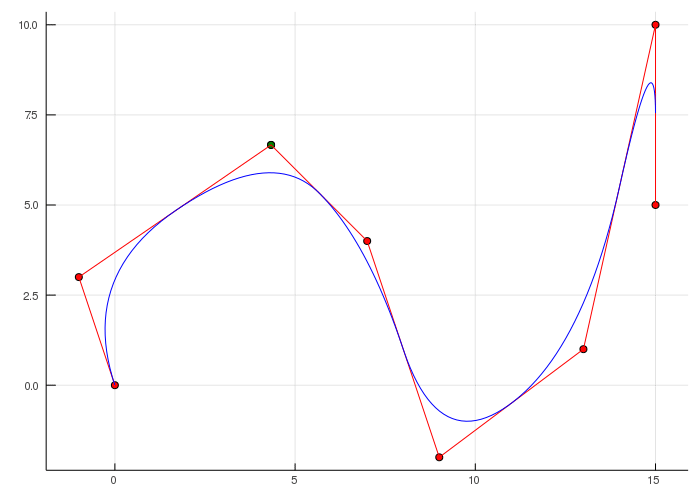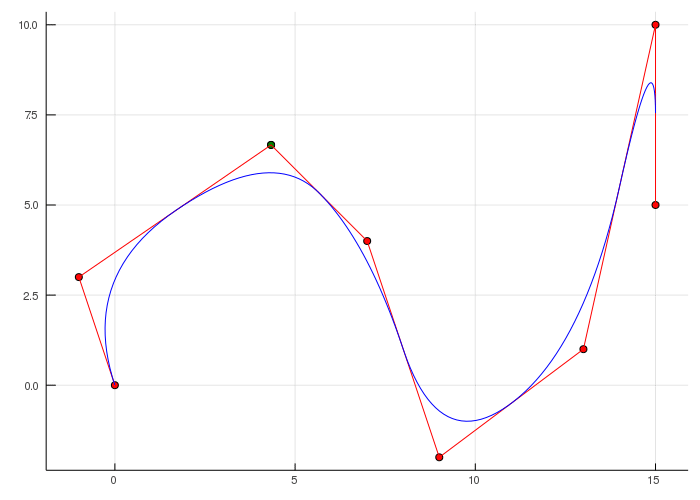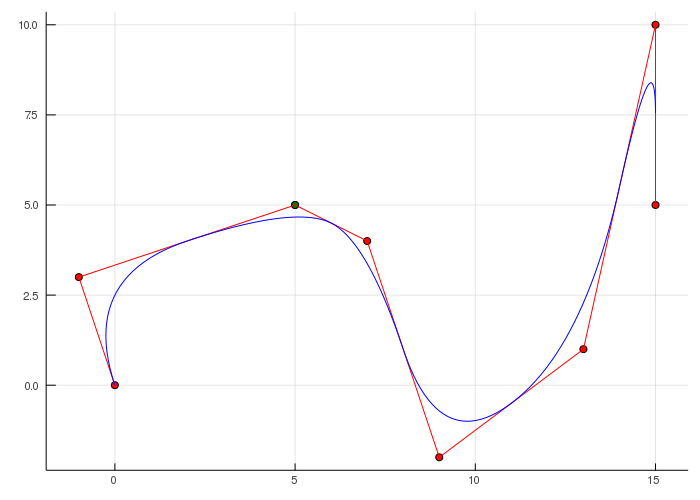
Сплайны — это математические функции, позволяющие создавать плавные кривые путем соединения ряда контрольных точек. Сплайны позволяют гибко изменять форму кривой, обеспечивая непрерывность и плавность между соседними сегментами.
Для создания сплайна обычно используется набор контрольных точек, определяющих траекторию кривой. Кривая строится путем интерполяции или аппроксимации пути между этими контрольными точками с помощью базисных функций, таких как B-сплайны или кривые Безье.
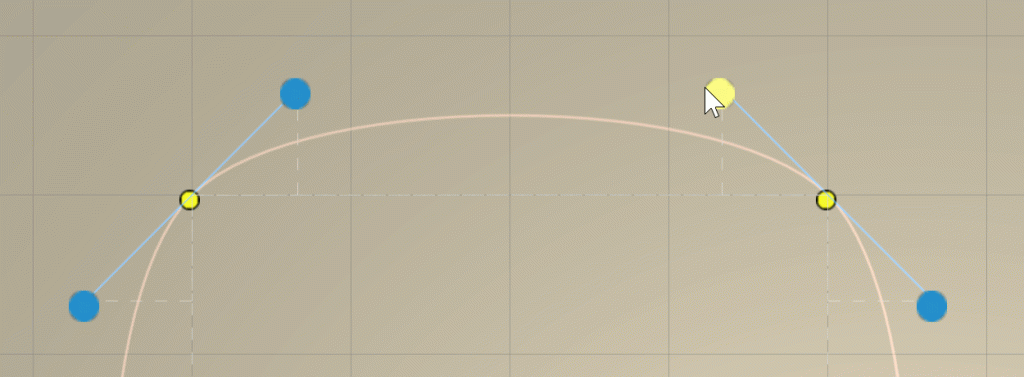
Сплайны — это универсальный инструмент для точного и гибкого представления сложных кривых или поверхностей, что делает их неоценимыми в различных областях.
Но как сплайны используются и применяются в архитектуре KAN?
Упрощенное объяснение принципа действия KAN
KAN отличаются от традиционных MLP тем, что заменяют фиксированные функции активации на обучаемые функции (B-сплайны) по краям сети.
Эта адаптивная архитектура позволяет KAN эффективно моделировать сложные функции, сохраняя при этом интерпретируемость и уменьшая количество необходимых параметров.
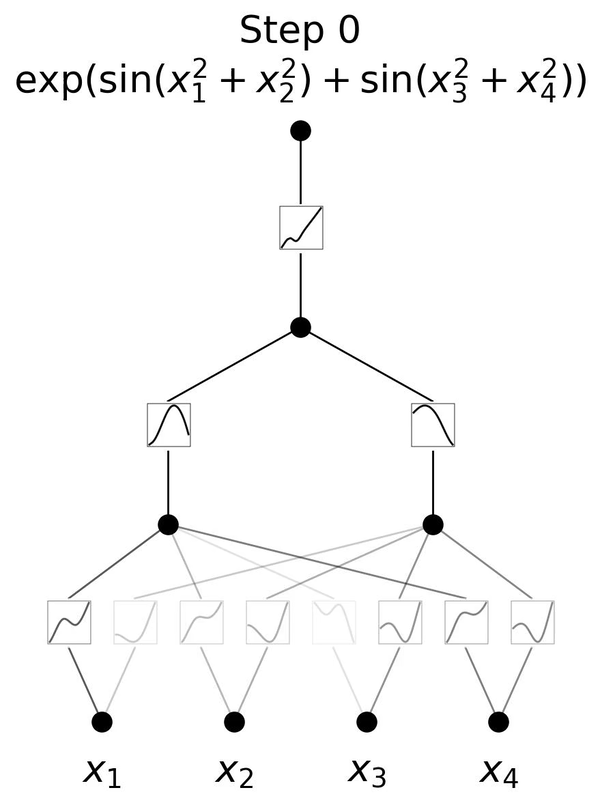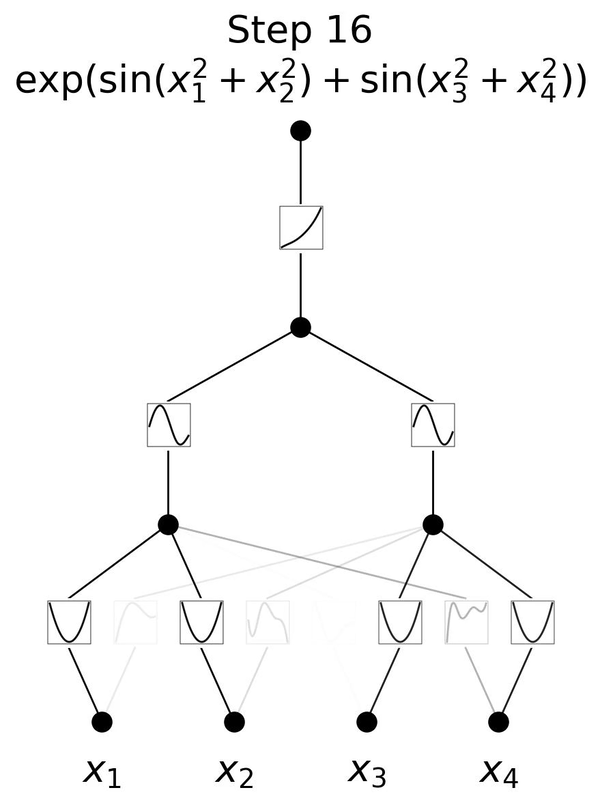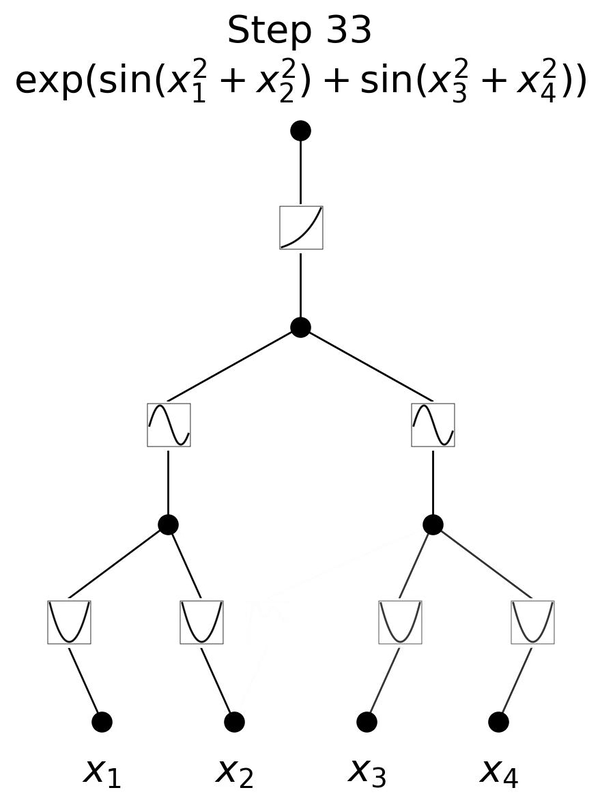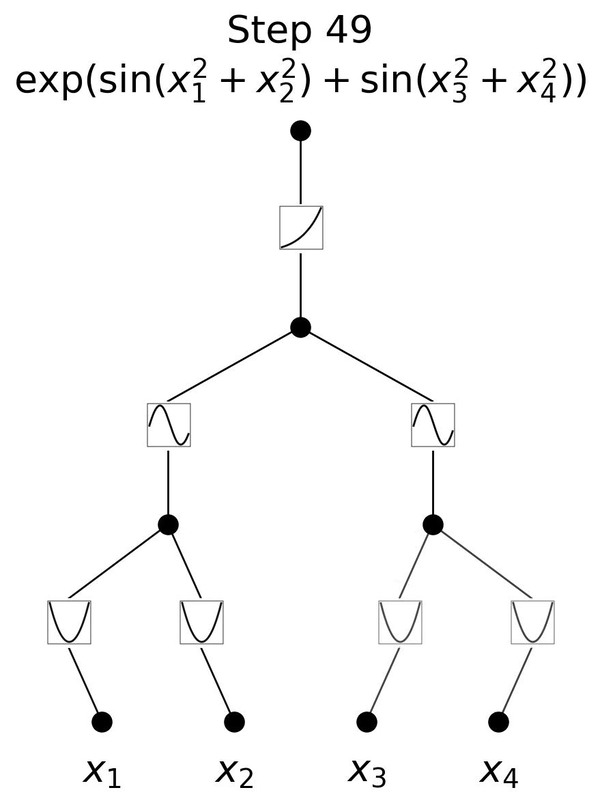
В отличие от своих аналогов в MLP, служащих пассивными каналами для передачи сигналов, нейроны в KAN являются активными участниками процесса обучения, предназначенными для динамического формирования своего поведения в ответ на данные, с которыми они сталкиваются.
Этот трансформационный сдвиг стал возможен благодаря использованию обучаемых функций активации, расположенных на краях сети.
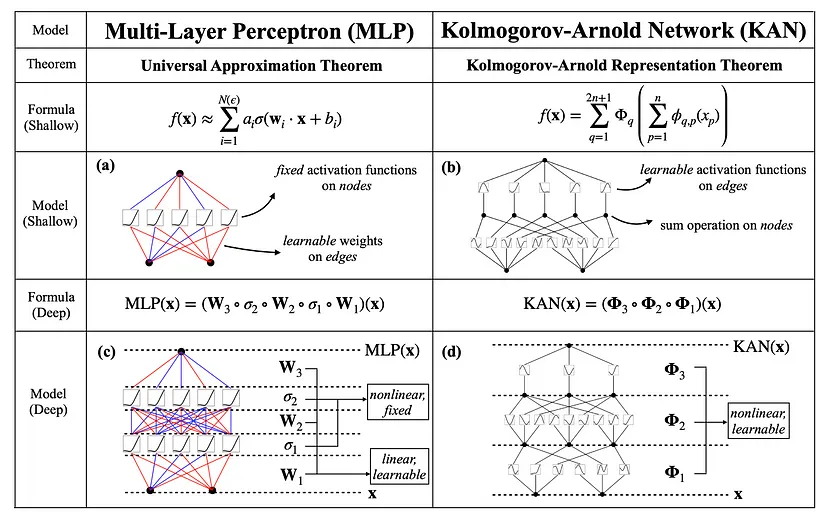
Используя экспрессивную мощь B-сплайнов, эти функции придают KAN беспрецедентную гибкость и адаптивность, позволяя ей с легкостью ориентироваться в сложных ландшафтах данных.
Основные преимущества KAN
Оптимизированная масштабируемость
KAN демонстрирует превосходную масштабируемость по сравнению с MLP, особенно в сценариях с высокоразмерными данными. Способность KAN раскладывать сложные функции на более простые компоненты позволяет эффективно обрабатывать большие наборы данных. Это делает KAN идеальной нейронной сетью для задач с огромными объемами информации.
Повышенная точность
Несмотря на использование меньшего количества параметров, KAN достигает более высокой точности и меньших потерь, чем традиционные MLP, при решении различных задач. Это объясняется способностью KAN адаптивно моделировать взаимосвязи внутри данных, что приводит к более точным предсказаниям и лучшим результатам обобщения при работе с невидимыми образцами.
Высокая степень интерпретируемости моделей
Структура KAN облегчает интерпретируемость, позволяя исследователям выводить символьные формулы, которые эффективно представляют изученные шаблоны. В отличие от моделей черного ящика, KAN дает представление о том, как входные функции преобразуются по всей сети, повышая прозрачность и улучшая понимание процесса.
Теперь мы знаем, что такое сети Колмогорова-Арнольда и почему они так важны в сфере искусственного интеллекта. Но мир движется не только благодаря теориям и моделям, которые хорошо смотрятся на бумаге.
Самое ценное в KAN — простота масштабирования и использования в задачах, связанных с наукой о данных, с помощью PyKAN — новой библиотеки Python.
Закончим обсуждение KAN примером реализации этой архитектуры на Python.
Python-реализация KAN в PyKAN
Для демонстрации выполним задачу классификации.
Создание набора данных
Создадим синтетический набор данных с помощью функции make_moons библиотеки sklearn.
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import torch
import numpy as np
dataset = {}
train_input, train_label = make_moons(n_samples=1000, shuffle=True, noise=0.1, random_state=None)
test_input, test_label = make_moons(n_samples=1000, shuffle=True, noise=0.1, random_state=None)
dataset['train_input'] = torch.from_numpy(train_input)
dataset['test_input'] = torch.from_numpy(test_input)
dataset['train_label'] = torch.from_numpy(train_label)
dataset['test_label'] = torch.from_numpy(test_label)
X = dataset['train_input']
y = dataset['train_label']
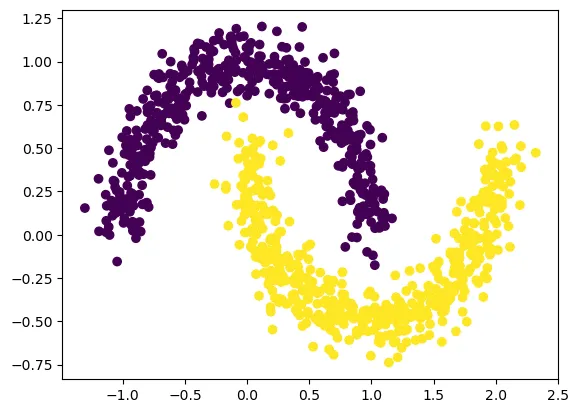
plt.scatter(X[:,0], X[:,1], c=y[:])
Выходные данные (визуализация набора данных)
Создание и обучение KAN
from kan import KAN
odel = KAN(width=[2,2], grid=3, k=3)
def train_acc():
return torch.mean((torch.argmax(model(dataset['train_input']),
dim=1) == dataset['train_label']).float())
def test_acc():
return torch.mean((torch.argmax(model(dataset['test_input']),
dim=1) == dataset['test_label']).float())
results = model.train(dataset, opt="LBFGS", steps=20,
metrics=(train_acc, test_acc),
loss_fn=torch.nn.CrossEntropyLoss())
Получение символьной формулы из модели
Далее выводится символьная формула, которая представляет то, что модель узнала из данных.
formula1, formula2 = model.symbolic_formula()[0]
Вычисление точности
Получаем точность из выведенной формулы.
def acc(formula1, formula2, X, y):
batch = X.shape[0]
correct = 0
for i in range(batch):
logit1 = np.array(formula1.subs('x_1',
X[i,0]).subs('x_2', X[i,1])).astype(np.float64)
logit2 = np.array(formula2.subs('x_1', X[i,0]).subs('x_2',
X[i,1])).astype(np.float64)
correct += (logit2 > logit1) == y[i]
return correct/batch
# Вывод точности
print('train acc of the formula:', acc(formula1,
formula2,
dataset['train_input'],
dataset['train_label']))
print('test acc of the formula:', acc(formula1,
formula2,
dataset['test_input'],
dataset['test_label']))
Вывод
train acc of the formula: tensor(0.9700)
test acc of the formula: tensor(0.9660)
Заключение
Сети Колмогорова-Арнольда представляют собой сдвиг парадигмы в архитектуре нейронных сетей. Хотя для полного раскрытия их потенциала необходимы дальнейшие исследования и эксперименты, KAN обещают стать ценным инструментом для развития машинного обучения и научных открытий в ближайшие годы.
Поскольку эта область продолжает развиваться, KAN стоят на переднем крае инноваций, формируя будущее интеллектуальных систем и революционизируя подход к анализу и моделированию сложных данных.
Читайте также:
- Сложные ИИ-модели созданы с помощью некачественных данных
- 3 лайфхака по работе с музыкальным ИИ в условиях нехватки данных
- Почему не стоит разрабатывать инструменты ИИ на основе чатов
Читайте нас в Telegram, VK и Дзен
Перевод статьи Manushi Mukhi: Kolmogorov–Arnold Networks (KAN) Are About To Change The AI World Forever