В сфере машинного обучения работа с высокоразмерными векторами не просто распространена — она необходима. Об этом свидетельствует архитектура таких популярных моделей, как трансформеры. Например, BERT — двунаправленная нейронная сеть-кодировщик — использует 768-мерные векторы для кодирования токенов входных последовательностей, которые она обрабатывает, и для улучшения распознавания сложных паттернов в данных. Учитывая, что наш мозг с трудом визуализирует все, что выходит за пределы трех измерений, использование 768-мерных векторов просто поражает воображение!
Высокоразмерные сценарии представляют собой множество проблем, хотя некоторые модели машинного, в том числе глубокого, обучения отлично справляются с ними. В этой статье рассмотрим понятие “проклятия размерности”, объясним некоторые интересные явления, связанные с ним, углубимся в математику, лежащую в основе этих явлений, и обсудим их общие последствия для моделей машинного обучения.
Подробные математические доказательства, связанные с этой статьей, доступны здесь.
Что такое “проклятие размерности”?
Некоторые полагают, что геометрические модели, знакомые нам в трехмерном пространстве, ведут себя аналогично в пространствах более высокой размерности. Это не так. При увеличении размерности возникает множество интересных и контринтуитивных явлений. “Проклятие размерности” — это термин, придуманный Ричардом Беллманом (известным математиком) для обозначения всех этих удивительных эффектов.
Особенность высокой размерности заключается в том, что “объем” пространства (скоро рассмотрим его более подробно) растет экспоненциально. Возьмем градуированную линию (в одном измерении) от 1 до 10. На этой линии находится 10 целых чисел. Продлим ее в 2 измерениях: теперь это квадрат с 10 × 10 = 100 точками с целочисленными координатами. Теперь представим себе “всего лишь” 80 измерений: у нас уже будет 10⁸⁰ точек, что равно количеству атомов во Вселенной.
Другими словами, с увеличением размерности объем пространства растет экспоненциально, в результате чего данные становятся все более разреженными.
Высокоразмерные пространства являются “пустыми”.
Рассмотрим другой пример. Необходимо вычислить наибольшее расстояние между двумя точками в единичном гиперкубе (где каждая сторона имеет длину 1).
- В 1 измерении (гиперкуб представляет собой отрезок прямой от 0 до 1) максимальное расстояние равно просто 1.
- В 2 измерениях (гиперкуб образует квадрат) максимальное расстояние — это расстояние между противоположными углами [0,0] и [1,1], которое равно √2, вычисляемому по теореме Пифагора.
- Если распространить это понятие на n измерений, то расстояние между точками в [0,0,…,0] и [1,1,…,1] будет равно √n. Эта формула объясняется тем, что каждое дополнительное измерение добавляет квадрат 1 к сумме под квадратным корнем (опять же по теореме Пифагора).
Интересно, что с увеличением числа измерений n наибольшее расстояние внутри гиперкуба растет со скоростью O(√n). Это явление иллюстрирует эффект убывающей отдачи, когда увеличение размерности пространства приводит к пропорционально меньшему увеличению пространственного расстояния. Более подробно этот эффект и его последствия будут рассмотрены в следующих разделах данной статьи.
Понятие расстояния в высокоразмерных пространствах
Углубимся в понятие расстояния.
В предыдущем разделе мы убедились в том, что высокоразмерные пространства делают понятие расстояния практически бессмысленным. Но что это значит на самом деле, и можно ли математически визуализировать это явление?
Проведем эксперимент, используя тот же n-мерный единичный гиперкуб, который мы определили ранее. Сначала сгенерируем набор данных путем случайной выборки множества точек в этом кубе: эффективно смоделируем многомерное равномерное распределение. Затем выберем другую точку (точку запроса) из этого распределения и понаблюдаем за расстоянием до ее ближайшего и самого дальнего соседа в нашем наборе данных.
Вот соответствующий код на языке Python:
def generate_data(dimension, num_points):
''' Generate random data points within [0, 1] for each coordinate in the given dimension '''
data = np.random.rand(num_points, dimension)
return data
def neighbors(data, query_point):
''' Returns the nearest and farthest point in data from query_point '''
nearest_distance = float('inf')
farthest_distance = 0
for point in data:
distance = np.linalg.norm(point - query_point)
if distance < nearest_distance:
nearest_distance = distance
if distance > farthest_distance:
farthest_distance = distance
return nearest_distance, farthest_distance
Можно также построить график этих расстояний:
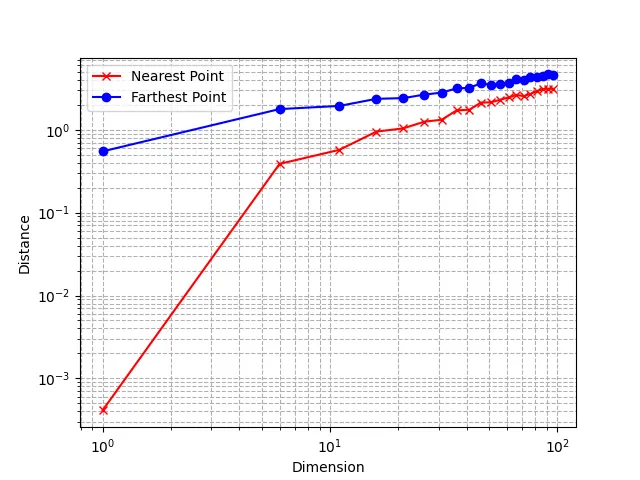
Использование логарифмической шкалы показывает, что относительная разница между расстоянием до ближайшего и самого дальнего соседа имеет тенденцию к уменьшению с увеличением размерности.
Это довольно контринтуитивное поведение: как объяснялось в предыдущем разделе, точки сильно удалены друг от друга из-за экспоненциально растущего объема пространства, но в то же время относительные расстояния между точками становятся меньше.
Понятие ближайших соседей исчезает.
Отсюда следует, что само понятие расстояния становится менее значимым и менее различимым по мере увеличения размерности пространства. Можете представить, какие проблемы это создает для алгоритмов машинного обучения (таких как kNN), полагающихся исключительно на расстояния.
Математика: n-мерный шар
Теперь рассмотрим некоторые другие интересные явления. Для этого нам понадобится n-мерный шар. n-мерный шар — обобщенная модель шара в n-мерном пространстве. n-мерным шаром с радиусом R называется совокупность точек, находящихся на расстоянии не более R от центра пространства 0.
Рассмотрим радиус 1. 1-мерный шар — это отрезок [-1, 1]. 2-мерный шар — это диск, ограниченный единичной окружностью, уравнение для которой — x² + y² ≤ 1. 3-мерный шар (то, что мы обычно называем “шаром”) имеет уравнение x² + y² + z² ≤ 1. Можно распространить это определение на любое измерение:
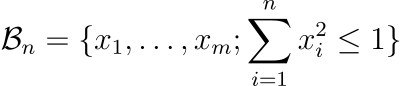
Возникает вопрос: каков объем этого шара? Это непростой вопрос и требует довольно много математических выкладок, которые не будут здесь изложены (подробное описание приводится здесь).
После долгих упражнений (интегрального исчисления) можно доказать, что объем n-мерного шара выражается следующим образом (где Γ обозначает гамма-функцию):
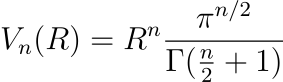
Например, при R = 1 и n = 2 объем равен πR², так как Γ(2) = 1. Это действительно “объем” 2-мерного шара (в этом случае его также называют “площадью” круга).
Однако помимо того, что объем n-мерного шара представляет собой интересную математическую задачу, он также обладает некоторыми удивительными свойствами.
С увеличением размерности n объем n-мерного шара стремится к 0.
Такое утверждение справедливо для любого радиуса, но для наглядности представим это явление на нескольких значениях R.
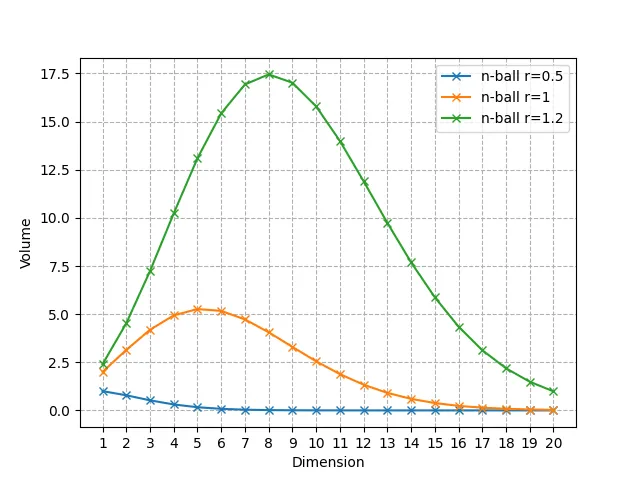
Как видите, он неукоснительно стремится к 0, но вначале увеличивается, а затем уменьшается до 0. При R = 1 шаром с наибольшим объемом является 5-мерный шар, а значение n, достигающее максимума, смещается вправо по мере увеличения R.
Вот первые значения объема единичного n-мерного шара, вплоть до n = 10.

Объем высокоразмерного единичного шара сосредоточен вблизи его поверхности.
При малых размерностях объем шара выглядит вполне “однородным”. В случае больших размерностей это не так.
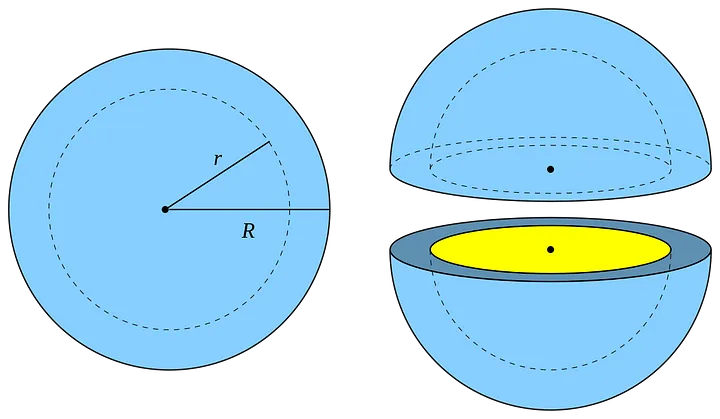
Рассмотрим n-мерный шар с радиусом R и другой шар с радиусом R-dR, где dR очень мал. Часть n-мерного шара между этими двумя шарами называется “оболочкой” и соответствует части шара вблизи его поверхности (см. визуализацию в 3D). Можно вычислить соотношение объема всего шара и объема только этой тонкой оболочки.
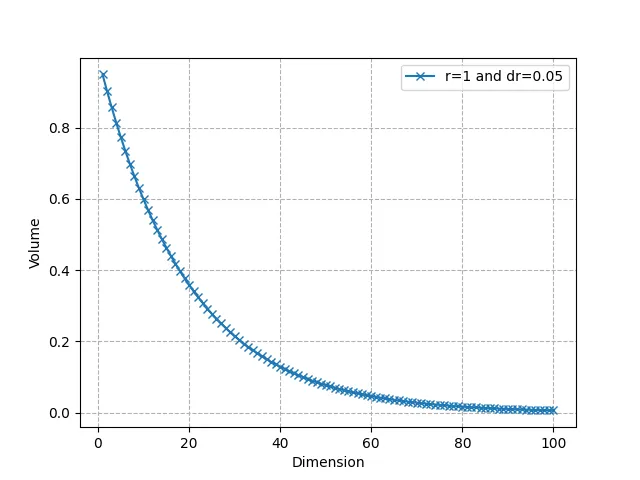
Как видим, оно очень быстро стремится к 0: в пространствах высокой размерности почти весь объем находится вблизи поверхности. Например, для R = 1, dR = 0,05 и n = 50 около 92,3% объема сосредоточено в тонкой оболочке, из чего следует, что в более высоких размерностях объем находится в “углах”. И снова это связано с искажением понятия расстояния, наблюдаемого нами ранее.
Обратите внимание, что объем единичного гиперкуба равен 2ⁿ. Единичная сфера практически “пуста” в очень высоких измерениях, в то время как у единичного гиперкуба, напротив, экспоненциально больше точек. Это еще раз доказывает, как идея “ближайшего соседа” точки теряет свою эффективность, поскольку при больших значениях n почти нет точек, находящихся на расстоянии R от запрашиваемой точки q.
“Проклятие размерности”, переобучение и бритва Оккама
“Проклятие размерности” тесно связано с принципом переобучения. Из-за экспоненциального роста объема пространства с увеличением размерности, нужны очень большие наборы данных, чтобы адекватно отразить и смоделировать высокоразмерные паттерны. Более того: чтобы преодолеть это ограничение, требуется количество образцов, возрастающее экспоненциально с увеличением размерности. Такой сценарий, характеризующийся большим количеством признаков при относительно небольшом количестве точек данных, особенно чреват переобучением.
Согласно принципу бритвы Оккама, простые модели обычно лучше сложных, так как они менее склонны к переобучению. Этот принцип особенно актуален в условиях высокой размерности (где играет роль “проклятие размерности”), поскольку поощряет снижение сложности модели.
Применение принципа бритвы Оккама в высокоразмерных сценариях может означать снижение размерности самой проблемы (с помощью таких методов, как PCA, отбор признаков и т. д.), тем самым минимизируя некоторые последствия “проклятия размерности”. Упрощение структуры модели или пространства признаков помогает справиться с разреженным распределением данных и вновь сделать метрики расстояния более значимыми. Например, уменьшение размерности является очень распространенным предварительным шагом перед применением алгоритма kNN (алгоритма получения k-ближайшего соседнего результата). Более современные методы, такие как ANNS (approximate nearest neighbor search — поиск ближайшего соседа), также являются способами работы с высокоразмерными сценариями.
Преимущества размерности
Использование высокоразмерных сценариев в машинном обучении, помимо описанных проблем, дает и некоторые преимущества.
- Высокая размерность может улучшить линейную сепарабельность, что делает более эффективными такие методы, как ядерный.
- Архитектуры глубокого обучения особенно успешно справляются с навигацией и извлечением сложных паттернов из высокоразмерных пространств.
Как и всегда в машинном обучении, приходится идти на компромисс: использование перечисленных преимуществ предполагает баланс между возрастающими вычислительными требованиями и потенциальным повышением производительности модели.
Заключение
Теперь вы представляете, насколько “странной” может быть геометрия в высокоразмерных пространствах и какие сложности она создает для разработки моделей машинного обучения. Данные в высокоразмерных пространствах очень разрежены, но при этом имеют тенденцию концентрироваться в углах, поэтому расстояния теряют свою значимость.
Хотя “проклятие размерности” указывает на существенные ограничения в высокоразмерных пространствах, интересно наблюдать, как современные модели глубокого обучения все эффективней справляются с этими сложностями. Например, эмбеддинг-модели и новейшие LLM используют высокоразмерные векторы для более эффективного выявления и моделирования текстовых паттернов.
Читайте также:
- Добавляем в приложение SwiftUI холст Freeform, чат и видеозвонки
- Работа с графиками в SwiftUI: руководство для начинающих
- Подробно об акторах в Swift
Читайте нас в Telegram, VK и Дзен
Перевод статьи Maxime Wolf: The Math Behind “The Curse of Dimensionality”





