Jackknife+ — это эффективный метод конформного прогнозирования, разработанный ведущими исследователями в области машинного обучения из Чикагского университета, Стэнфордского университета, Университета Карнеги-Меллона и Калифорнийского университета в Беркли. Информация о нем опубликована в работе “Predictive inference with the jackknife+” (“Прогнозируемый вывод с jackknife+”).
Метод jackknife был создан Морисом Кенуйем в 1949–1956 годах. Позже, в 1958 году, эту технику усовершенствовал известный статистик Джон Тьюки. Он предложил термин “jackknife” (“складной нож”) в качестве метафорического определения данного метода из-за его популярности и универсальности. Подобно физическому складному ножу — компактному и удобному, — этот статистический метод предлагает гибкое и адаптируемое решение для широкого спектра задач (несмотря на существование других инструментов, которые могут служить конкретным целям более эффективно).
Наша задача — построить функцию регрессии с помощью обучающих данных, которые включают пары признаков (Xi, Yi). Нам нужно предсказать выход Yn+1 для нового вектора признаков Xn+1=x и создать соответствующий интервал погрешности для этого предсказания. Предположительно данный интервал будет включать истинное значение Yn+1 с заранее определенной вероятностью охвата.
Прямой подход может заключаться в подгонке базовой регрессионной модели к обучающим данным, вычислении остатков и использовании этих остатков для оценки квантиля. Этот квантиль затем может быть использован для определения ширины интервала прогнозирования для новой тестовой точки. Однако такой подход имеет тенденцию недооценивать фактическую погрешность из-за чрезмерной подгонки: остатки, полученные из обучающего множества, обычно меньше, чем те, которые можно было бы получить на основе неизвестных тестовых данных.
Для минимизации проблемы чрезмерной подгонки и был разработан надежный статистический метод, получивший название “jackknife”. Изначально он предназначался для уменьшения предвзятости и получения оценки дисперсии. Он основан на принципе последовательного исключения из набора данных каждого наблюдения и повторной оценки модели. Такая методика позволяет эмпирическим путем оценить устойчивость модели и ее чувствительность к отдельным точкам данных.
Процедура jackknife проиллюстрирована на рисунке ниже.
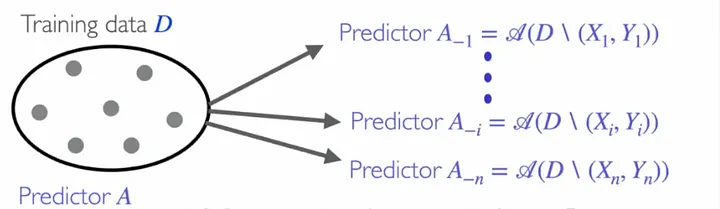
В каждом случае регрессии jackknife модель подгоняется ко всем точкам данных, исключая пару (Xi, Yi). Это позволяет вычислить остатки метода leave-one-out. Интерпретируя такие остатки как несоответствия, мы можем оценить квантиль и определить интервалы прогнозирования, как в случае индуктивного конформного прогнозирования. Поскольку данный метод борется с избыточной подгонкой, используя для вычислений остатки вне выборки, теоретически ожидается, что он обеспечит адекватный охват.
Однако на практике способность охвата процедуры jackknife может давать сбои, особенно при работе с сильно искаженными данными или данными с “тяжелыми хвостами”. Несмотря на то что существуют подтверждения, свидетельствующие об успешных результатах в асимптотических условиях или при устойчивости алгоритма регрессии jackknife, очевидно, что метод jackknife может утратить прогностический потенциал охвата в ситуациях, когда оценка неустойчива.
В некоторых случаях метод jackknife может даже давать нулевой охват. Это означает, что оцененный интервал прогноза не содержит истинного значения. Кроме того, следует отметить, что метод jackknife может быть трудоемким в вычислительном плане, так как требует многократной подгонки модели на уменьшенном наборе данных.
Эти ограничения привели к разработке усовершенствованного метода, известного как jackknife+. Улучшенная версия направлена на оптимизацию способности охвата и вычислительной эффективности традиционного метода jackknife. Она вошла в семейство методов конформного прогнозирования, унаследовав все их преимущества, такие как гарантия валидности даже на конечных выборках любого размера, отсутствие распределений и применимость к любой регрессионной модели.

Отличием методов jackknife и jackknife+ с точки зрения построения интервалов прогнозирования является использование в последнем методе в тестовой точке leave-one-out-прогнозов. Это делается для учета изменчивости подогнанной функции регрессии, дополняя квантили leave-one-out-остатков, используемых в методе jackknife. Такое усовершенствование позволяет методу jackknife+ обеспечивать надежные гарантии охвата независимо от распределения точек данных и для любого алгоритма, симметрично обрабатывающего точки обучения. Напротив, оригинальный метод jackknife не дает таких теоретических гарантий без предпосылок устойчивости и в некоторых ситуациях может демонстрировать неудовлетворительные свойства охвата.
Метод jackknife+ имеет некоторое сходство с кросс-конформным прогнозированием, предложенным Владимиром Вовком, поскольку оба направлены на построение интервалов прогнозирования, обеспечивающих надежные гарантии охвата независимо от распределения точек данных. Они работают с любым алгоритмом, в котором точки обучения рассматриваются симметрично.
Однако метод jackknife+ отличается тем, что для учета изменчивости подогнанной функции регрессии в тестовой точке используются leave-one-out-прогнозы, а также квантили leave-one-out-остатков, как при кросс-конформном прогнозировании.
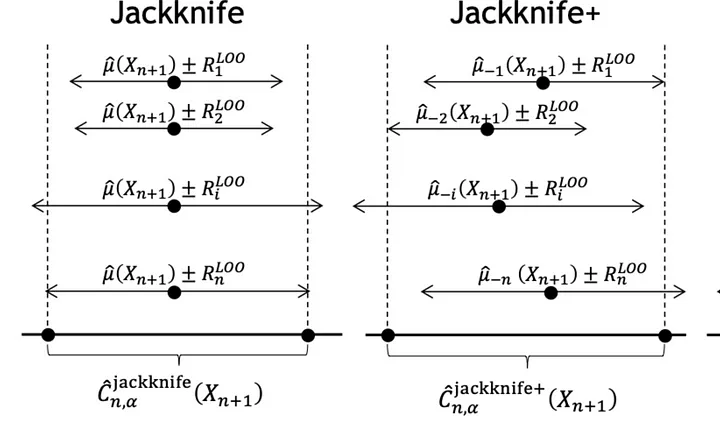
На рисунке ниже показана разница между интервалами прогнозирования, полученными методами jackknife и jackknife+. В отличие от метода jackknife, который строит интервалы прогнозирования вокруг прогноза, сделанного на тестовой точке с использованием всего набора данных, метод jackknife+ генерирует “n” точечных оценок. Вокруг этих оценок строятся интервалы прогнозирования модели leave-one-out. Поэтому jackknife+ применяет квантили к этим “n” индивидуальным интервалам прогнозирования, построенным с помощью процедуры jackknife+, а не к остаткам, как в методе jackknife.
Jackknife+ доступен в библиотеке MAPIE с открытым исходным кодом Conformal Prediction.
Читайте также:
- Искусственный интеллект и наше будущее
- #03TheNotSoToughML | Регрессия: Ошибки → Спуск с вершины горы
- Различные модели машинного обучения
Читайте нас в Telegram, VK и Дзен
Перевод статьи Valeriy Manokhin: Jackknife+ — a Swiss knife of Conformal Prediction for regression






