Нейронные сети обучаются путем итеративной настройки параметров (весов и смещений) на этапе обучения. В начале параметры инициализируются случайно сгенерированными весами, а смещения устанавливаются равными нулю. Затем данные пропускаются через сеть в прямом направлении, чтобы получить выходные данные модели. И наконец, выполняется обратное распространение. Процесс обучения модели обычно включает в себя несколько итераций прямого прохода, обратного распространения и обновления параметров.
В этой статье мы поговорим о том, как обратное распространение обновляет параметры после прямого прохода, и рассмотрим простой, но подробный пример обратного распространения. Прежде чем приступить, определимся с данными и архитектурой, которые будем использовать.
Данные и архитектура
Набор данных содержит три признака, а целевой класс имеет только два значения — 1 для прохода и 0 для ошибки. Задача состоит в том, чтобы отнести точку данных к одной из двух категорий, т. е. выполнить двоичную классификацию. Мы будем использовать только один обучающий пример для большей понятности.
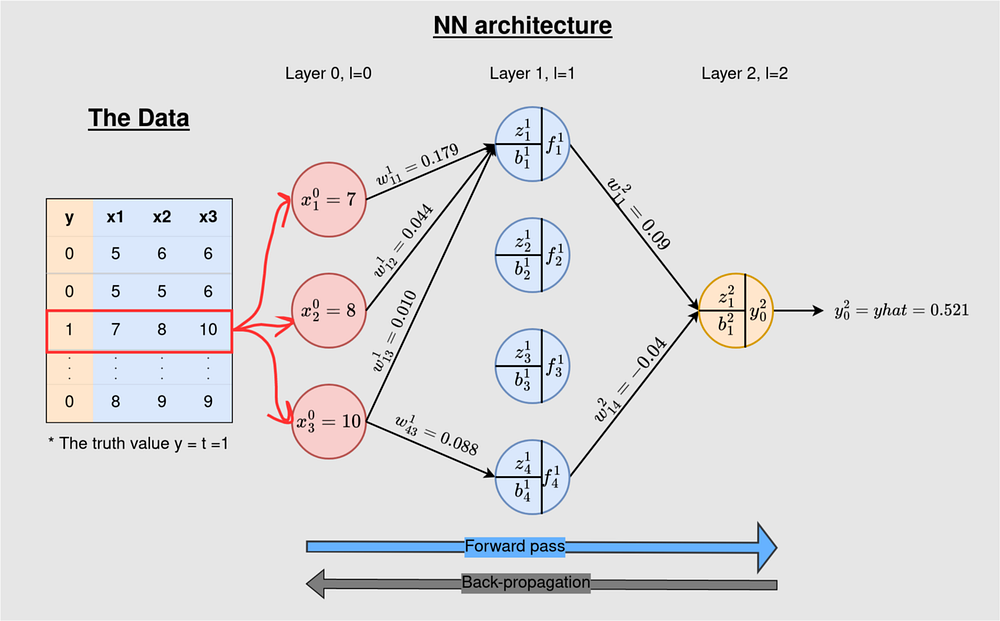
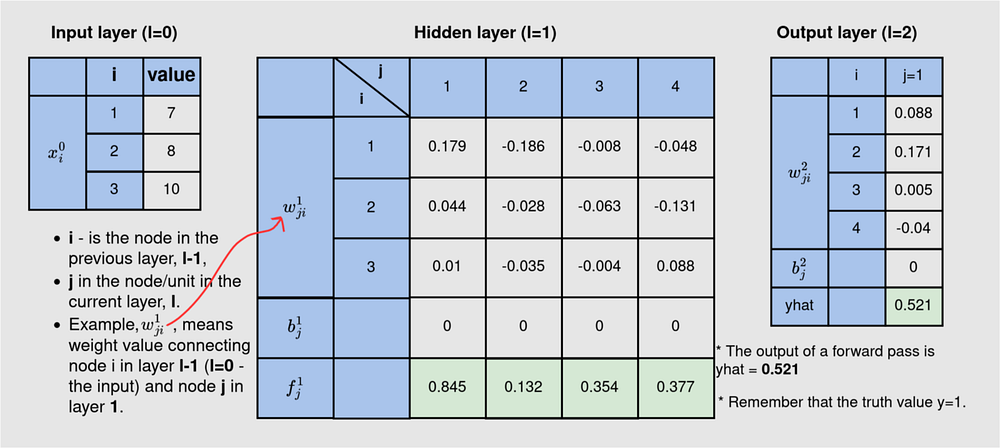
На рисунке 1 показаны данные и архитектура нейронной сети, которые мы будем использовать. Обучающий пример помечен соответствующим фактическим значением 1. Эта нейронная сеть 3-4-1 является сетью с плотной связью: каждый узел в текущем слое связан со всеми нейронами в предыдущем слое, за исключением входного. Однако мы исключили некоторые связи, чтобы излишне не нагружать рисунок. Прямой проход дает на выходе 0,521.
Важно понимать: прямой проход позволяет информации идти в одном направлении — от входного к выходному слою, а обратное распространение выполняет противоположную задачу. Оно проводит данные от выхода назад, обновляя параметры (веса и смещения).
Обратное распространение — метод контролируемого обучения, используемый в нейронных сетях для обновления параметров, чтобы сделать прогнозы сети более точными. Процесс оптимизации параметров осуществляется с помощью алгоритма оптимизации, называемого градиентным спуском (мы разберем это понятие чуть ниже).
Прямой проход дает прогноз (yhat) цели (y) с потерями, которые фиксируются функцией затрат (E), определенной как:
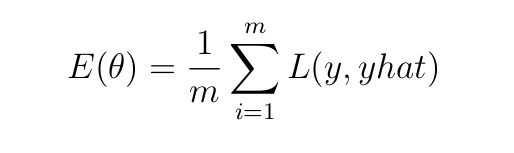
Здесь m — количество примеров обучения, а L — ошибка/потери, возникающие при предсказании моделью значения yhat вместо фактического значения y. Целью является минимизация затрат E. Это достигается путем дифференцирования E относительно параметров (wrt, весов и параметров) и регулировки параметров в направлении, противоположном градиенту (поэтому алгоритм оптимизации называется градиентным спуском).
В этой статье мы рассматриваем обратное распространение на примере обучения 1 (m=1). При таком рассмотрении E сводится к следующему уравнению:
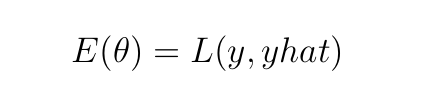
Выбор функции потерь L
Функция потерь L определяется в зависимости от поставленной задачи. Для задач классификации подходящими функциями потерь являются кросс-энтропия (также известная как логарифмическая функция потерь) и кусочно-линейная функция потерь, тогда как для задач регрессии подходят такие функции потерь, как средняя квадратичная ошибка (MSE) и средняя абсолютная ошибка (MAE).
Кросс-энтропия — функция, подходящая для данной задачи двоичной классификации (данные имеют два класса, 0 и 1). Кросс-энтропия как функция потерь для двоичной классификации может быть применена к данному примеру прямого прохода на Рисунке 1, как показано ниже:
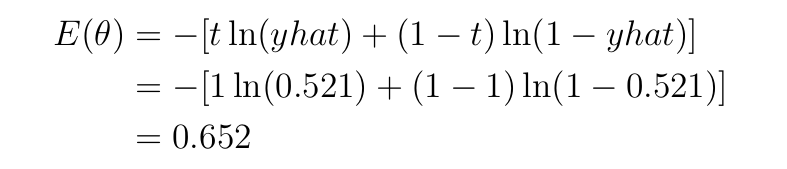
Здесь t=1 — истинная метка, yhat=0,521 — выход модели, а ln — натуральный логарифм по основанию 2.
Поскольку теперь мы понимаем архитектуру нейронной сети и функцию затрат, которую будем использовать, можем перейти непосредственно к рассмотрению шагов проведения обратного распространения.
Данные и параметры
В таблице ниже приведены данные по всем слоям нейронной сети 3–4–1. На 3-нейронном входе указаны значения из данных, которые мы предоставляем модели для обучения. Второй/скрытый слой содержит веса (w) и смещения (b), которые нужно обновить, а выход (f) на каждом из 4 нейронов во время прямого прохода. Выход содержит параметры (w и b) и выход модели (yhat) — это значение фактически является прогнозом модели на каждой итерации обучения модели. После одного прохода вперед yhat=0,521.
A. Уравнения обновления и функция потерь
Важно! Вспомните информацию из предыдущего раздела: E(θ)=L(y, yhat), где θ — это параметры (веса и смещения). То есть, E — это функция от y и yhat, а yhat=g(wx+b), следовательно, yhat — это функция от w и b. x — переменная данных, а g — функция активации. E является функцией w и b и, следовательно, может быть дифференцирована относительно этих параметров.
Параметры на каждом слое обновляются с помощью следующих уравнений:
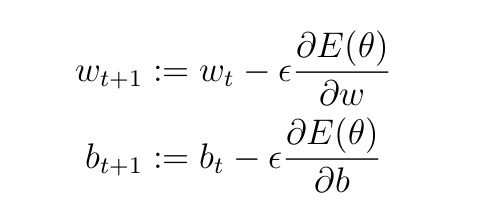
Здесь t — шаг обучения, ϵ — скорость обучения (гиперпараметр, задаваемый пользователем). Он определяет скорость обновления весов и смещений. Мы будем использовать ϵ=0,5 (это произвольный выбор).
Из уравнений 4 получаются следующие обновленные суммы
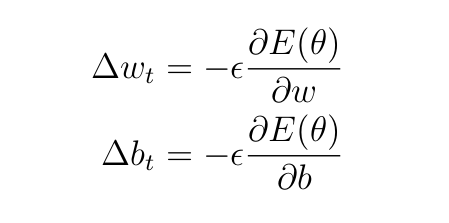
Как было сказано ранее, поскольку мы работаем с двоичной классификацией, мы будем использовать в качестве функции потерь кросс-энтропию, определяемую как:
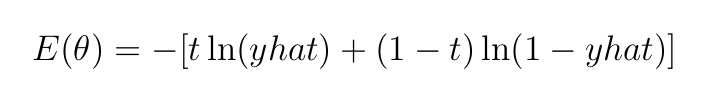
Мы будем использовать сигмоидную активацию для всех слоев:
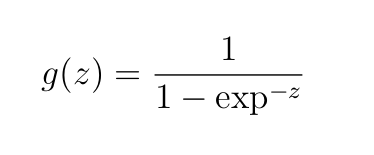
Здесь z=wx+b — взвешенный вход в нейрон плюс смещение.
B. Обновление параметров на выходном скрытом слое
В отличие от прямого прохода, обратное распространение работает в обратном направлении от выходного слоя к слою 1. Нам нужно вычислить производные/градиенты относительно параметров для всех слоев. Для этого нужно понять цепное правило дифференцирования.
Цепное правило дифференцирования гласит, что если y=f(u) и u=g(x), т. е. y=f(g(x))), то производная от y в отношении x будет равна:
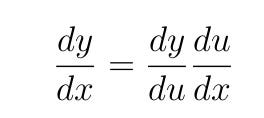
Проще говоря, нужно поработать над производной внешней функции, прежде чем переходить к внутренней.
В нашем случае мы имеем:
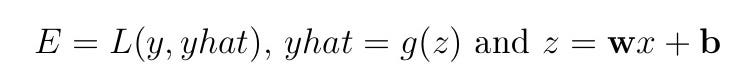
Возьмем в работу пример обновления w²₁₁ и b²₁. Будем следовать маршрутам, показанным ниже.
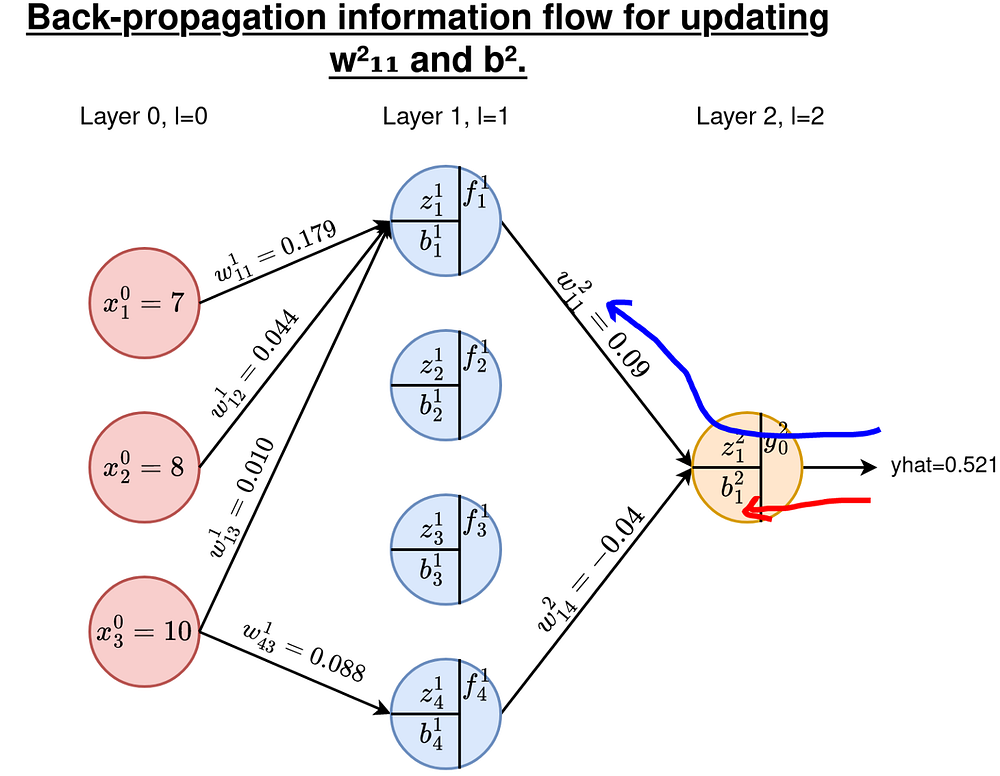
B1. Вычисление производных для весов
По цепному правилу дифференцирования имеем:

Примечание: при оценке приведенных выше производных относительно w²₁₁ все остальные параметры рассматриваются как константы, т. е. w²₁₂, w²₁₃, w²₁₄ и b²₁. Производная от константы равна 0, поэтому некоторые значения были исключены в приведенной выше производной.
Далее приведена производная сигмоидной функции.
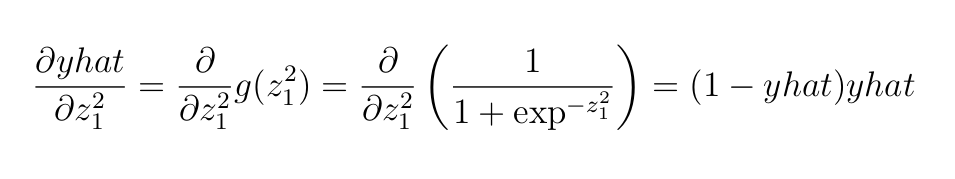
Далее — производная функции потерь кросс-энтропии.

Производные по отношению к трем другим весам на выходном слое следующие (можете проверить):
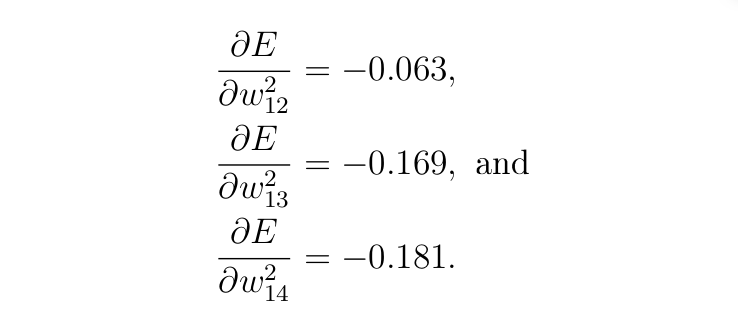
B2. Вычисление производных для смещения
Нам нужно вычислить:
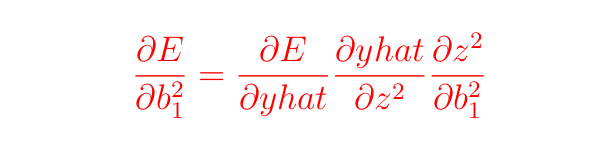
В предыдущих разделах мы уже вычислили ∂E и ∂yhat, осталось только выполнить следующие действия:
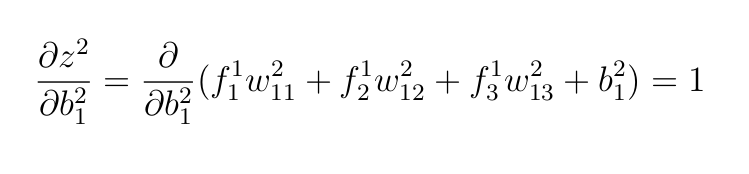
Мы использовали те же аргументы, что и раньше. Все остальные переменные, кроме b²₁, считаются константами, поэтому при дифференцировании они уменьшают 0.

До сих пор мы вычисляли градиенты относительно всех параметров на слоях “выход-вход”.
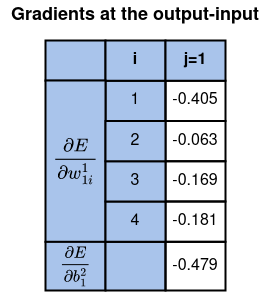
На данном этапе мы уже готовы обновить все веса и смещения на слоях “выход-вход”.
B3. Обновление параметров на слоях “выход-вход”

Вычислите остальные значения таким же образом и сверьте их с таблицей ниже.
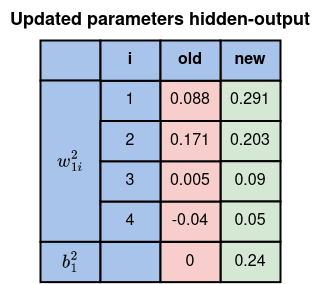
C. Обновление параметров на слое “скрытый-выход”
Как и раньше, нам нужны производные E относительно всех весов и смещений на этих слоях. Всего у нас есть 4x3=12 весов для обновления и 4 смещения. В качестве примера возьмем w¹₄₃ и b¹₂. Маршруты показаны на рисунке ниже.
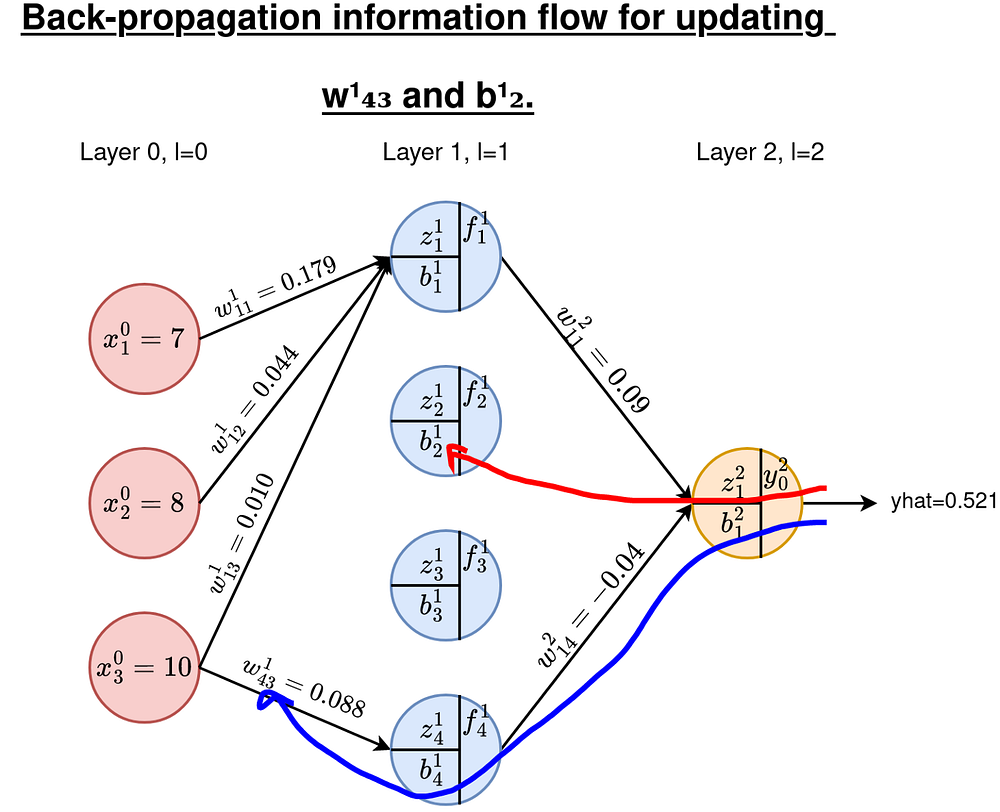
C1. Градиенты весов
Для весов нам нужно вычислить производную (следуйте по маршруту на Рисунке 6, если следующее уравнение покажется вам слишком сложным):
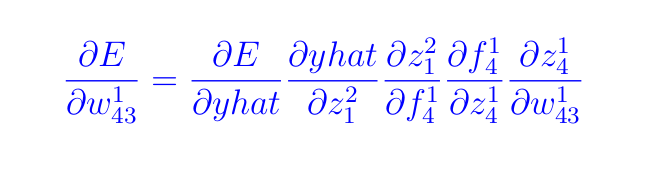
По мере того, как мы будем проходить через каждую из приведенных выше производных, обратите внимание на следующие важные моменты.
- На выходе модели (при нахождении производной
Eпо отношению кyhat) мы фактически дифференцируем функцию потерь. - На выходах слоев (
f), где мы дифференцируем wrtz, мы находим производную функции активации. - В двух вышеприведенных случаях дифференцирование относительно весов и смещений данного нейрона дает одинаковые результаты.
- Взвешенные входы (
z) дифференцируются относительно параметров (wиb), которые нужно обновить. В этом случае все параметры остаются постоянными, кроме интересующего нас параметра.
Выполнив тот же процесс, что и в разделе B, получаем следующее.
- Взвешенные входы для слоя
1:
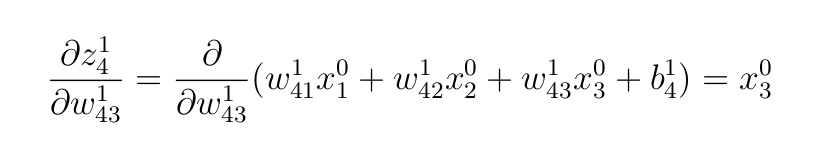
- Производную сигмоидной функции активации, примененной к первому слою:
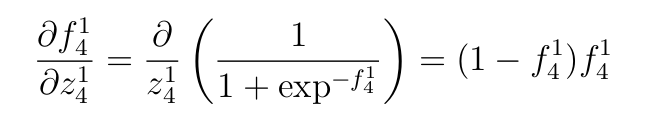
- Взвешенные входы выходного слоя.
f-значения — выходы скрытого слоя:
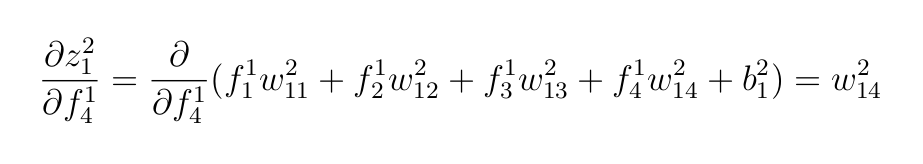
- Функцию активации, применяемую к выходу последнего слоя:
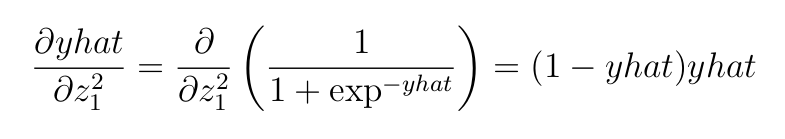
- Производную функции потерь кросс-энтропии для двоичной классификации (wrt по отношению к
yhat):
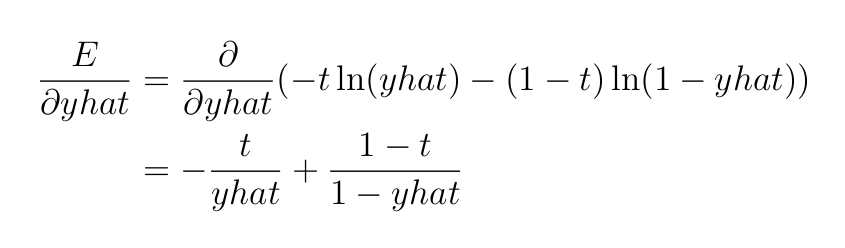
Мы можем объединить все это в следующее уравнение:
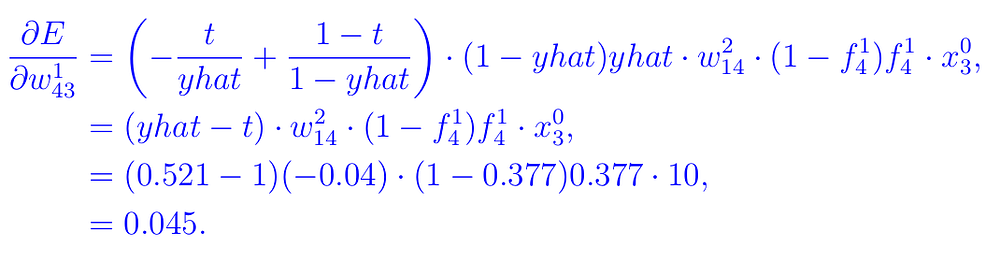
C2. Градиенты смещения
Используя те же понятия к b¹₂ мы имеем:

Все значения градиентов для слоев “скрытый-вход” приведены в таблице ниже:
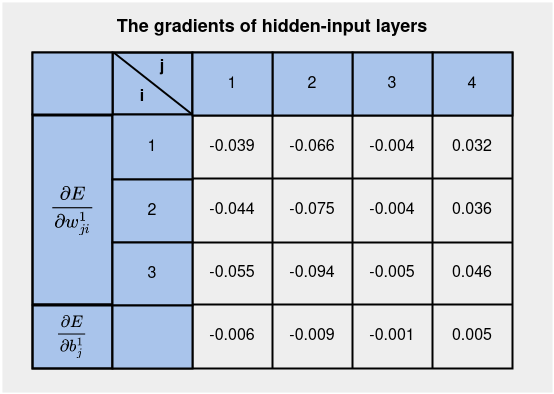
На этом этапе мы готовы к вычислению обновленных параметров на слоях “скрытый-вход”.
C3. Обновление параметров на слоях “скрытый-вход”
Вернемся к уравнениям обновления и поработаем над обновлением параметров w¹₁₃ и b¹₃.
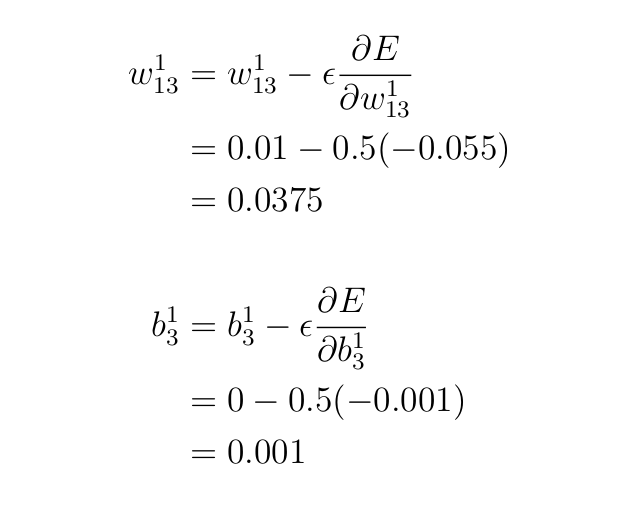
Итак, сколько же параметров нужно обновить?
У нас есть 4x3=12 весов и 4x1=4 смещения на слоях “скрытый-вход”, а также 4x1=4 веса и 1 смещение на слоях “выход-скрытый”. Это в общей сложности 21 параметр. Они называются обучаемыми параметрами.
Все обновленные параметры для слоев “скрытый-вход” показаны ниже:
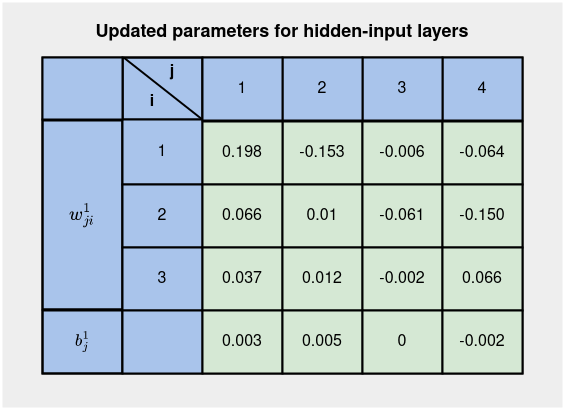
Теперь у нас есть обновленные параметры для всех слоев на Рисунке 8 и Рисунке 5 благодаря обратному распространению ошибки. Выполнение прямого прохода с этими обновленными параметрами дает прогноз модели: yhat, равный 0,648 по сравнению с 0,521. Это означает, что модель обучается — приближается к истинному значению 1 после двух итераций обучения. Другие итерации дают результаты 0,758, 0,836, 0,881, 0,908 и 0,925.
Определения
- Эпоха. Одна эпоха — процесс, при котором весь набор данных проходит через сеть один раз. Она включает в себя один инстанс прямого прохода и обратного распространения.
- Размер пакета. Это количество примеров обучения, одновременно пропущенных через сеть. В данном случае у нас один пример обучения. При наличии большого набора данных их можно пропускать через сеть пакетами.
- Количество итераций. Одна итерация равна одному проходу с использованием примеров обучения, заданных в качестве размера пакета. Один проход — это прямой проход и обратное распространение.
Пример. Если у нас есть 2000 примеров обучения и задан размер пакета 20, то для завершения 1 эпохи потребуется 100 итераций.
Заключение
В этой статье мы рассмотрели обратное распространение на примере. Мы увидели, как цепное правило дифференцирования используется для получения градиентов различных уравнений — функции потерь, функции активации, уравнений взвешивания и уравнений выходного слоя. Мы также обсудили, как можно использовать производную по отношению к функции потерь для обновления параметров на каждом слое.
Читайте также:
- Сегментация изображений с использованием сети обратного внимания
- Оценка производительности нейронной сети Keras с помощью визуализаций Yellowbrick
- Извините, но мы не можем воскресить вас
Читайте нас в Telegram, VK и Дзен
Перевод статьи Kiprono Elijah Koech: How Does Back-Propagation Work in Neural Networks?