В большинстве описаний среднеквадратичной ошибки (mean square errore, MSE) упускается один важнейший нюанс: метрики и функции потерь — это не совсем одно и то же. Для оценки и оптимизации производительности модели в машинном обучении нужны две отдельные функции потерь. MSE может быть либо тем, либо другим, либо третьим — выбор за исследователем.
Чтобы было понятнее, что имеется в виду под оценкой производительности и оптимизацией, вместо отвлеченных рассуждений обратимся к конкретным примерам. Для демонстрации будем использовать среднеквадратичную ошибку (MSE), но имейте в виду: MSE — это полезная метрика, но не панацея. Итак, погрузимся в тему!
Что такое MSE?
Среднеквадратичная ошибка (MSE) — одна из множества метрик, которые используются для оценки эффективности модели. Для расчета MSE необходимо возвести в квадрат количество обнаруженных ошибок и найти среднее значение.
Зачем вычислять MSE?
Это можно сделать для 2 целей.
- Оценка производительности — визуальное определение того, насколько хорошо работает модель. Другими словами, это возможность быстро понять, с чем предстоит работать.
- Оптимизация модели позволяет выяснить, достигнуто ли наилучшее из возможных соответствий или же требуются улучшения. Другими словами, определить, какая модель максимально подходит для работы с выбранными точками данных.
Если вы предпочитаете учиться на видео, переходите по этой ссылке (англ. язык):
Оценка производительности (метрика)
Цель оценки производительности заключается в том, чтобы человек мог составить представление об эффективности модели.
Метрика производительности показывает, насколько хорошо работает модель. К слову, “модель” — это просто популярное слово для “инструкции”, а инструкция “хороша”, если при введении исходных данных обеспечивает результат, близкий к ожидаемому. Метрика позволяет оценить, насколько близки результаты модели к ожидаемым (причем исследователь сам должен определить, что значит “близки”). MSE — это всего лишь одна из многих возможных метрик.
Если модель совершенна, MSE = 0.
Откуда берется MSE? Мы вычисляем эту метрику, находя ошибки, которые допустила модель. Поэтому она является функцией ошибочности. Чем ниже MSE, тем лучше работает модель. Когда ошибок совсем нет, MSE = 0. Беглый взгляд на MSE дает представление о том, насколько хорошо модель соответствует или не соответствует данным.
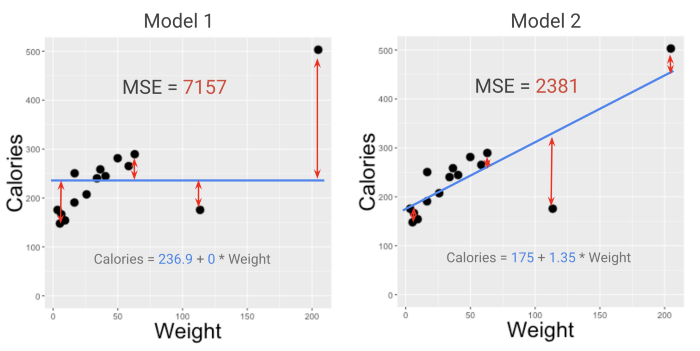
Взглянув на MSE двух моделей из примера со смузи в моем курсе (смотрите видео здесь), можно легко определить фаворита. Модель с меньшим MSE (2381, а не 7157) лучше подходит к данным. Но что означают эти цифры?
Метрики должны быть рассчитаны так, чтобы иметь смысл для людей и эффективно передавать информацию.
Приведенные выше значения MSE не очень удобны для осмысления. Это проблема, если нужна достаточно информативная метрика. Метрики должны быть рассчитаны так, чтобы иметь смысл для людей и эффективно передавать информацию. Можно ли улучшить значение MSE?
Да, конечно. Вот вам RMSE!
Для оценки производительности модели (на глаз) RMSE часто является лучшим выбором, чем MSE. RMSE — это просто корень квадратный из MSE (R означает root, “корень”).
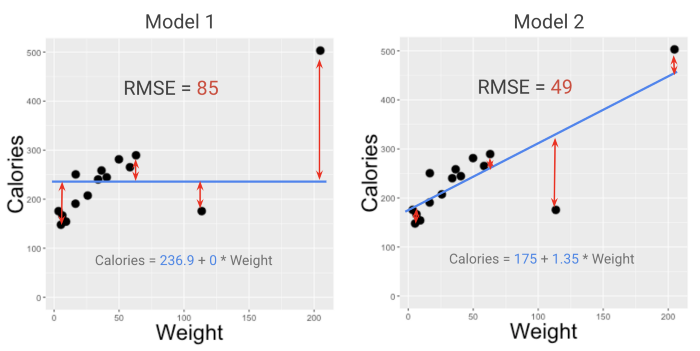
При поиске более подходящей метрики, исследователи предпочитают RMSE, потому что она переводит MSE в более понятную для человека шкалу. Это не совсем то, что покажет, “насколько велики наши ошибки в среднем”, но достаточно близко к тому, что можно принять во внимание, чтобы предотвратить риски.
Исследователи предпочитают RMSE, потому что эта метрика переводит MSE в более удобную для восприятия шкалу.
Но что если вы настаиваете на еще более точной метрике — той, что даст корректное представление о среднем размере ошибок? В таком случае можно воспользоваться метрикой, называемой средним абсолютным отклонением или MAD (mean absolute deviation). Иногда ее также называют MAE (mean absolute error).
Чтобы вычислить MAD, нужно просто игнорировать знаки (“+” и “-”) перед значениями всех ошибок и найти среднее значение. В отличие от RMSE, MAD является абсолютным выражением среднего размера ошибок.
MAD показывает, насколько ошибочна модель в среднем.
MAD — лучшая метрика производительности по сравнению с RMSE, потому что ее легче понять и связать с процессом оптимизации. Она более значима для исследователя и понятнее для человека. Но подходит ли она для машин?
Оптимизация модели (функция потерь)
Вторая цель использования MSE — это оптимизация модели. Здесь в дело вступают функции потерь.
Функция потерь — это формула, которую алгоритм машинного обучения пытается минимизировать на этапе оптимизации/подгонки модели. Разложим это понятие по полочкам.
Фрагмент из курса MFML для тех, кому нужно освежить в памяти понятие оптимизации модели
Предположим, планируется использование одного из самых простых алгоритмов МО — OLS (ordinary least squares, метод простых наименьших квадратов). Это означает, что модель, с которой предстоит работать, обладает простейшей формой — прямой линией.
Линия, проведенная через данные, имеет наклон и точку пересечения с координатной осью. Установка этих двух параметров зависит от вас!
Y = точка пересечения + наклон * X
Рациональный подход требует выбора модели, которая лучше всего подходит для работы с исходными данными. Другими словами, оптимальным выбором будет модель, которая максимально адаптирована к исходным данным. Следовательно, нужна функция оценки, которая становится больше, когда модель подходит хуже, и меньше — в обратном случае.
Эта функция позволит изменять параметры точки пересечения и наклона, наблюдая за изменением оценки. Такую функцию оценки называют “функцией потерь” — чем больше потери, тем хуже модель.
Ошибочность? Заядлые перфекционисты уверены: ошибки — это плохо. Поэтому выразим ошибочность в терминах наших ошибок. Любая функция потерь, которая становится больше, когда больше ошибок, подойдет? Технически — да. Практически — нет.
Вот как это работает, если выбрать MSE в качестве функции потерь: цель оптимизации — найти точку пересечения и наклон, которые дают как можно более низкое значение MSE. Как это происходит, показано в видео ниже.
Не стоит искать оптимальное значение MSE методом проб и ошибок (перебирание различных комбинаций наклона и точки пересечения вручную — медленный и скучный процесс).
Получить мгновенный результат позволят вычисления или алгоритм оптимизации, которые подскажут, какими должны быть необходимые параметры. Что касается алгоритмов оптимизации, то вам, скорей всего, не придется разрабатывать их с нуля. Наверняка будет возможность импортировать те, которые кто-то другой уже создал. Чаще всего с MSE очень удобно работать.
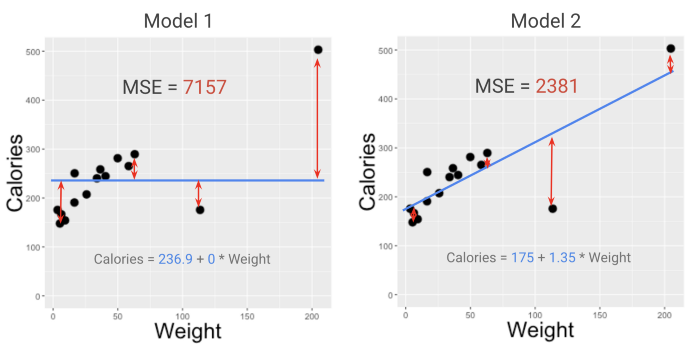
Что же происходит “за кулисами”? Есть формула, которая указывает, где именно должна располагаться линия, чтобы значение MSE было минимальным. Запускаемому коду даже не нужно постепенно приближаться к решению — он просто использует эту формулу, чтобы точно указать наклон и точку пересечения, наилучшие из возможных для работы линейной модели с данными.
Читайте также:
- Наука о данных простым языком
- #03TheNotSoToughML | Регрессия: Ошибки → Спуск с вершины горы
- Топ-10 ошибок анализа данных
Читайте нас в Telegram, VK и Дзен
Перевод статьи Cassie Kozyrkov: How to Use the MSE in Data Science