
В начале реализации проекта по исследованию данных важно обнаружить и обработать выбросы. В этом заключается одна из задач эксплораторного анализа данных.
Мы рассмотрим три метода обнаружения выбросов. Но прежде выясним, что такое выброс, заглянув в Википедию:
Выброс (в статистике) — это измерительная точка данных, которая значительно выделяется из общей выборки. Выбросы могут быть вызваны вариативностью измерений или указывать на экспериментальную ошибку; в последнем случае они иногда исключаются из набора данных. Выброс может вызвать серьезные проблемы при статистическом анализе.
Итак, выброс — это данные, которые имеют слишком высокое или слишком низкое значение по отношению к другим исследуемым данным. Конечно, в наборе данных может быть несколько выбросов, поэтому приходится неоднократно исключать их из набора данных. В противном случае выбросы способны вызывать статистические проблемы в анализе данных.
Но каковы критерии исключения выбросов? Чтобы ответить на этот вопрос, рассмотрим три метода обнаружения выбросов.
1. Графический подход
Этот подход дает исследователю возможность самому принимать решение. Как уже отмечалось, зачастую приходится неоднократно удалять выбросы из набора данных, а поскольку этот подход является графическим, то визуализация данных позволяет специалисту решить, какие выбросы удалять. Более того, он сам решает, какие данные считать выбросами, просто наблюдая за графом.
Рассмотрим пару примеров, взятых из моих проектов.
Допустим, у нас есть датафрейм под названием cons. Создадим диаграмму рассеяния с помощью Seaborn:
import seaborn as sns
#построение диаграммы рассеяния
sns.relplot(data=food, x='mean', y='latitude')
#определение размера фигуры
sns.set(rc={'figure.figsize':(30,15)})
#разметка
plt.title(f'MEAN PRODUCTION PER LATITUDE', fontsize=16) #название графика
plt.xlabel('Mean production [1000 tons]', fontsize=14) #метка x-оси
plt.ylabel('Latitude', fontsize=14) #метка y-оси
#показ сетки для лучшей визуализации
sns.set_style("ticks",{'axes.grid' : True})
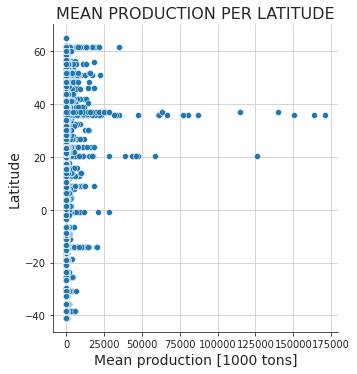
Не вдаваясь в значения параметров latitude (“интервал”) и mean production (“средняя производительность”), просто посмотрите на данные: какие точки считаете выбросами? Здесь ясно видно, что выбросы — “более высокие” числа. Исходя из этого, можно решить, что выбросы — это точки, чьи значения больше 75 000 или даже 50 000. Решайте сами, но принимайте решение на основе целостного анализа (одного этого графа недостаточно).
Это был один из графических методов обнаружения выбросов. Есть и другой — построение диаграммы размаха. Рассмотрим его на примере из одного из моих проектов.
Допустим, у нас есть датафрейм под названием phase. Нам нужно построить диаграмму размаха:
import seaborn as sns
#диаграмма размаха
sns.boxplot(data=phase, x='month', y='time')
#разметка
plt.title(f"BOXPLOT", fontsize=16) #название графика
plt.xlabel("MONTH", fontsize=14) #метка x-оси
plt.ylabel("CYCLE TIME[m]", fontsize=14) #метка y-оси
#добавление горизонтальной линии к среднему времени цикла
plt.axhline(mean, color="red")
red_line = mpatches.Patch(color="red",
label=f"mean value: {mean:.1f} [m]")
#обработка легенды
plt.legend(handles=[red_line],prop={"size":12})
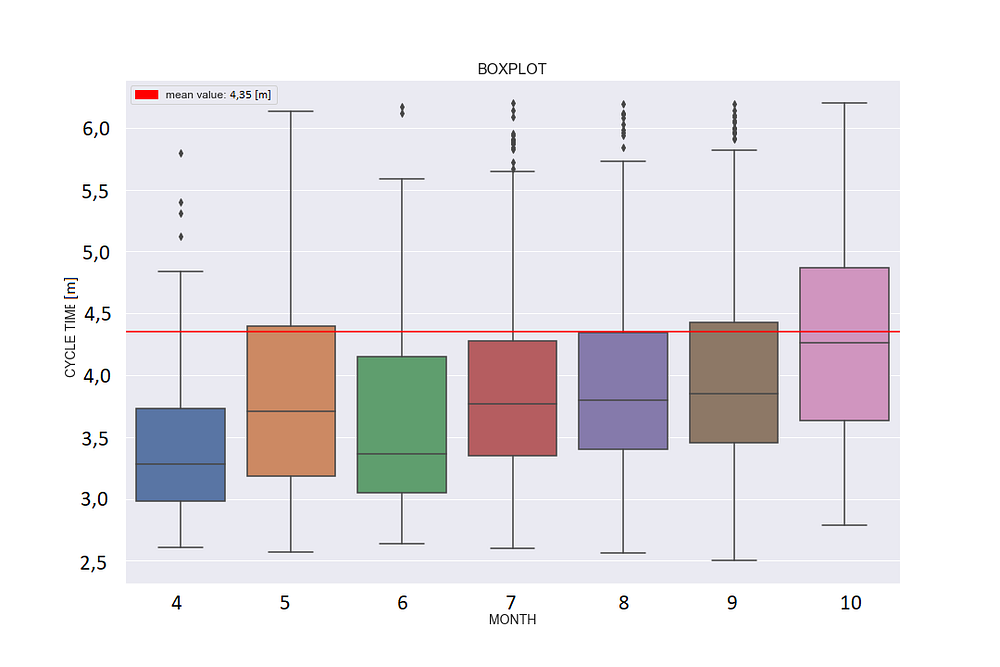
Снова рассмотрим график, не обращая внимания на то, что означают x и y. Здесь выбросами также являются только те данные, у которых значения “выше” (маленькие участки). Диаграмма размаха оставляет исследователю меньше возможностей контроля — выбросы здесь определяются на основе статистики. В данном случае это те точки, у которых значения больше максимального.
В диаграмме размаха максимальное значение рассчитывается как Q3+1.5*IQR, где IQR — это межквартильный размах. Он определяется по формуле IQR=Q3-Q1, где Q1 — первый квартиль, а Q3 — третий квартиль.
Как видите, использование этого графического метода не позволяет исследователю самому решать, какие точки считать выбросами. На помощь ему приходит статистическая (графическая) методика определения того, какие значения можно принимать за выбросы.
У обоих приведенных здесь графических методов есть один большой недостаток: их можно использовать только с двумерными данными. Это означает, что они подходят для случаев, когда у исследователя имеется только один столбец, представляющий вход, и другой, представляющий выход.
Если же будет 20 столбцов, представляющих входные данные, и один — выходные, то при использовании графического метода придется построить 20 графов. А если будет 100 столбцов, представляющих входные данные? Нужно понимать, что при всей эффективности графических методов, они могут использоваться не во всех ситуациях.
2. Метод Z-оценки
Z-оценка, или “стандартная оценка”, — это статистическая мера, которая показывает, на сколько стандартных отклонений наблюдаемая точка удалена от среднего значения.
Например, Z-оценка 1,2 означает, что точка данных находится на расстоянии 1,2 стандартного отклонения от среднего значения.
При использовании этого метода необходимо определить порог: если точка данных имеет значение, превышающее пороговое, то она является выбросом.
Вычисляем Z следующим образом:
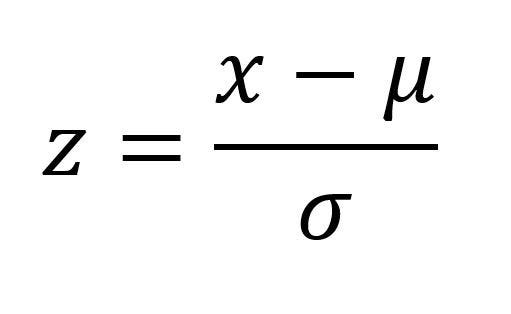
В этой формуле:
- X — значение точки данных;
- μ — среднее значение;
- σ — стандартное отклонение.
Приведем пример. Предположим, что у нас есть такие числа:
import numpy as np
#случайные данные
data = [1, 2, 2, 2, 3, 1, 1, 15, 2, 2, 2, 3, 1, 1, 2]
#вычисление среднего значения
mean = np.mean(data)
#вычисление стандартного отклонения
std = np.std(data)
#вывод значений
print(f'the mean is: {mean: .2f}')
print(f'the standard deviation ins:{std: .2f}')
-----------------
>>>
the mean is: 2.67
the standard deviation ins: 3.36
Установим порог для определения выбросов следующим образом:
#порог
threshold = 3
#список выбросов
outlier = []
#обнаружение выбросов
for i in data:
z = (i-mean)/std
if z > threshold:
outlier.append(i)
print(f'the outliers are: {outlier}')
-----------------
>>>
the outliers are: [15]
Можно использовать stats.zscore из библиотеки Scipy, которая применяется к массиву Numpy и датафреймам. Рассмотрим пример с датафреймом:
import pandas as pd
import scipy.stats as stats
#создание датафрейма
data = pd.DataFrame(np.random.randint(0, 10, size=(5, 3)), columns=['A', 'B', 'C'])
#z-оценка
data.apply(stats.zscore)
----------------
>>>
A B C
0 -0.392232 -0.707107 0.500000
1 -0.392232 -0.353553 -1.166667
2 1.568929 1.767767 1.333333
3 -1.372813 -1.060660 -1.166667
4 0.588348 0.353553 0.500000
В этом случае также нужно определить порог и решить, какие значения удалить.
Метод Z-оценки имеет несколько недостатков.
- Его можно использовать только с одномерными данными (один столбец датафреймов, массивов, списков и т. д.).
- Он должен использоваться только с нормально распределенными данными.
- Исследователю придется определить порог, зависящий от данных.
3. Изолирующий лес
Чтобы разобраться с понятием “изолирующий лес”, снова обратимся к Википедии:
Изолирующий лес — это алгоритм обнаружения аномалий. Он обнаруживает аномалии, используя изолированность (насколько далеко точка данных находится от остальных данных), а не моделируя нормальные точки.
Углубляясь в это понятие, можно отметить, что алгоритм “изолирующий лес” построен на основе древовидной структуры данных, аналогично алгоритму “случайный лес”, и не является моделью супервизорного управления, поскольку в нем нет заранее заданных меток. Это не что иное, как ансамбль бинарных деревьев решений, где каждое дерево называется “изолирующим деревом”.
Это означает, что алгоритм “изолирующий лес” работает со случайной выборкой данных, которые обрабатываются в древовидной структуре на основе случайно выбранных признаков. Образцы, которые проникают глубже в дерево, с меньшей вероятностью являются аномалиями, поскольку для их изолированности требуется больше срезов.
Возьмем для примера известный набор данных diabetes, предоставленный scikit-learn:
from sklearn.datasets import load_diabetes #импортирование данных from sklearn.ensemble import IsolationForest #импортирование алгоритма “изолирующий лес” #импортирование набора данных diab = load_diabetes() #определение признака и метки X = diab['data'] y = diab['target'] #creating dataframe df = pd.DataFrame(X, columns=["age","sex","bmi","bp", "tc", "ldl", "hdl","tch", "ltg", "glu"]) #проверка формы df.shape ------------------ >>> (442, 10)
Итак, этот датафрейм имеет 442 строки и 10 столбцов. Теперь воспользуемся алгоритмом “изолирующий лес”:
#идентифицирование выбросов
iso = IsolationForest()
y_outliers = iso.fit_predict(df)
#отбрасывание строк с выбросами
for i in range(len(y_outliers)):
if y_outliers[i] == -1:
df.drop(i, inplace = True)
#проверка новой формы датафрейма
df.shape
---------------------
>>>
(388, 10)
Как видите, количество строк уменьшилось, потому что были отброшены строки с выбросами.
Обратите внимание, что в этом примере был использован ансамбль, а не модель супервизорного управления. Это означает, что если снова запустить весь код, то конечная форма (форма датафрейма после отбрасывания строк с выбросами) может отличаться от полученной выше с 388 строками (попробуйте сами в качестве упражнения).
Алгоритм “изолирующий лес” не оставляет исследователю никакой возможности контролировать данные (это не модель супервизорного управления). Однако он является единственным из трех методов, рассмотренных в этой статье, позволяющим обрабатывать (и отбрасывать) выбросы в многомерных датафреймах. Он предоставляет возможность работать со всем набором данных, не уменьшая его.
Заключение
Рассмотрев три метода обнаружения выбросов, мы убедились в том, что лишь изолирующий лес позволяет работать с многомерными данными. Поэтому его и следует использовать в большинстве случаев. Если же вам придется исследовать совсем простой набор данных, можете прибегнуть к графическому методу или воспользоваться Z-оценкой.
Читайте также:
- 3 худших совета по осваиванию науки о данных
- Как легко и быстро создать веб-приложение на базе МО с помощью Python
- 5 видов регрессии и их свойства
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Federico Trotta: How To Detect Outliers in a Data Science Project






