Искусственная нейронная сеть (ИНС), по сути, является математической моделью сети нейронов человеческого мозга. Это позволяет нам думать о нейронах ИНС как об активированных или неактивированных, а также об их взаимодействии, подобном эффекту бабочки, когда включение в работу каждого отдельного нейрона зависит от состоянии всех его сетевых предшественников.
В чем ИНС и неврология расходятся, так это в самом понятии нейрона. С точки зрения искусственного интеллекта нейроны рассматривают как узлы, содержащие или временно хранящие данные, такие как float, и “синапсы”, соединяющие эти узлы в качестве весов, определяющих силу активации каждого нейрона.
Чтобы визуально представить себе простую нейронную сеть, взгляните на изображение ниже.
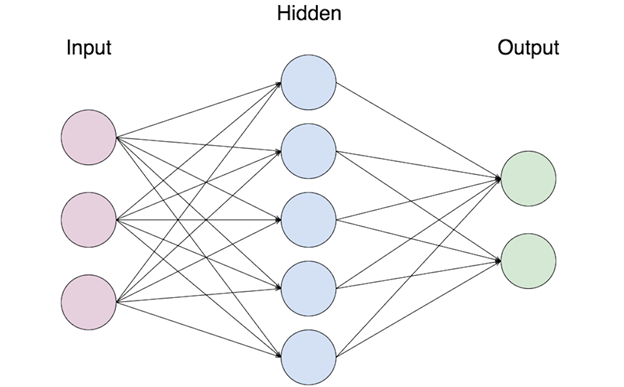
На этом изображении нейроны показаны кружками. Первый слой сети содержит 3 нейрона, второй (он же скрытый) — 5 нейронов, последний — 2 нейрона. Стало быть, общее количество нейронов в этой сети — 10. Подробнее о слоях поговорим позже.
Линии, соединяющие нейроны, указывают на вес. Сами веса представляют собой присвоенные числовые значения, выражающие силу связи между каждой парой узлов. Чем больше вес, тем сильнее связь, или корреляция, между двумя нейронами.
Веса особенно важно учитывать, поскольку они напрямую влияют на выходные данные узла. Выход любого нейрона представляет собой взвешенную сумму всех подключенных к нему входов.
Глядя на изображение ниже, попробуем выяснить, как выходные данные нейронной сети коррелируют с определенными входными данными и весами.
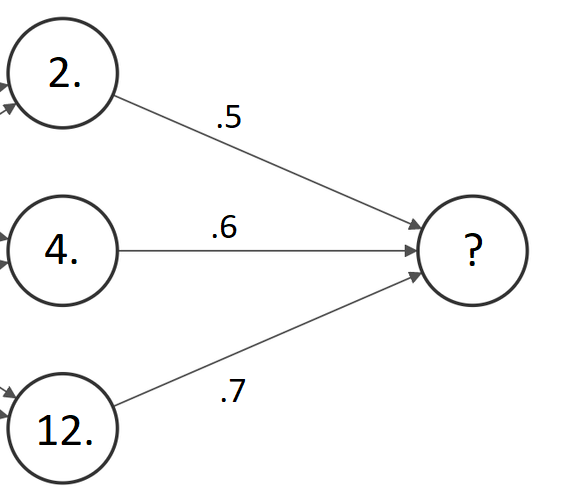
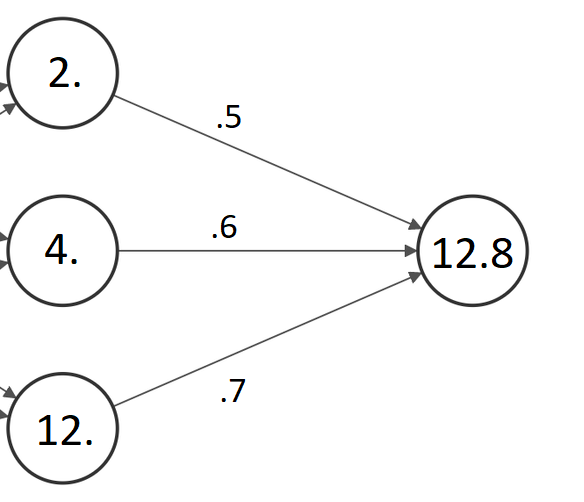
Итак, судя по изображению, нейрон, выход которого мы попытаемся найти, соединен с тремя нейронами в предыдущем слое с выходными данными 2, 4 и 12 соответственно. Эти три нейрона соединились с искомым нейроном в следующем слое весами .5, .6 и .7 соответственно. Чтобы узнать, каким будет выход искомого нейрона, надо умножить числовое значение, присвоенное каждому нейрону, на его вес, а затем вычислить сумму. Следовательно, выход данного нейрона будет равен (2 x .5) + (4 x .6) + (12 x .7), что составляет 12,8.
Слои, которых мы кратко коснулись ранее, образуют основу, или структуру, нейронной сети. Слои можно рассматривать как столбцы нейронов, которые соединены весами с предыдущим и последующим слоями. Положение слоя в нейронной сети определяет как его название, так и назначение.
Первый слой в нейронной сети известен как входной. Нейроны этого слоя представляют компоненты данных, которые нейронная сеть использует для изучения и прогнозирования.
Последний слой в нейронной сети известен как выходной. С ним связан процесс прогнозирования. Если учесть, что нейронная сеть классифицирует данные, в выходном слое будет по одному нейрону для каждой возможной категории входных данных. К примеру, если мы обучаем модель классификации изображений автомобилей и грузовиков, нам понадобятся два нейрона в выходном слое, чтобы представить две возможные категории, под которые могут подпадать наши данные.
Остальные слои, расположенные между входным и выходным слоями, называются скрытыми. Количество скрытых слоев, а также количество нейронов в каждом из них определяется произвольно. Это означает, что программист может экспериментировать и настраивать различные комбинации, пытаясь определить, что лучше всего подходит для конкретной модели.
Скрытые слои позволяют модели извлекать из входных данных функции, необходимые для распознавания шаблонов, чтобы с их помощью классифицировать различные входные данные.
Важно признать, что существует множество типов скрытых слоев, которые влияют на различные операции, выполняемые между слоями, и каждый из них может быть полезен в зависимости от поставленной задачи. Среди скрытых слоев наиболее часто используются так называемые плотные слои. Они отличаются тем, что все нейроны одного слоя соединены со всеми нейронами последующего. Это именно тот тип слоев, который был представлен в нашем первом примере.
Как бы впечатляюще ни выглядела нейронная сеть, невольно возникает вопрос: “Может ли столь хаотичная система учиться или производить что-либо вообще толковое!” Отличный вопрос! Нейронные сети действительно обучаются, адаптируя веса в процессе своего обучения, чтобы отобразить входные данные в определенной классификации.
Как нейронные сети достигают этого? Большинство нейронных сетей, а именно контролируемые ИНС, снабжены метками для данных, на которых они обучаются. В конце каждого прохождения через сеть модель вычисляет, насколько неверным было ее прогнозирование. Коэффициент неточности модели, называемый потерями модели (model’s loss), можно рассчитать многими способами. Затем модели используют оптимизаторы, такие как стохастический градиентный спуск. Оптимизатор принимает функцию потерь, созданную для каждого нейрона, и постепенно корректирует веса. В результате находится минимум функции потерь, что уменьшает общую погрешность модели.
Чтобы было понятнее, обратимся к аналогии. Представьте себе, что нейронная сеть играет в плинко. Задача модели, в зависимости от того, где был размещен чип, состоит в том, чтобы настроить колышки так, чтобы чип попадал в свой конкретный слот как можно чаще.

Искусственные нейронные сети, едва заявив о себе, быстро стали одной из самых “горячих” тем в информатике. Такая популярность объясняется прежде всего способностью нейросети оперативно улавливать закономерности в массиве данных. Это обернулось многочисленными преимуществами почти для каждой отрасли индустрии. Сегодня нейронные сети стремительно развиваются, закрепившись в качестве ключевых элементов машинного обучения, от классификаторов изображений до автокодировщиков и GAN.
Для закрепления этой темы рекомендую посмотреть захватывающее видео 3blue1brown’s с элементами анимации и подробным описанием основных понятий.
Читайте также:
- Рекуррентная нейронная сеть с головы до ног
- Нейронная сеть с нуля при помощи numpy
- Глубокие свёрточные нейросети: руководство для начинающих
Читайте нас в Telegram, VK и Дзен
Перевод статьи Matthew Farah, Neural Networks, in a Nutshell






