
Перед прочтением
В этой статье предполагается, что у читателя уже есть базовые знания о глубоких нейронных сетях (нейронных сетях прямого распространения). О них подробно рассказывалось в предыдущей статье. Очень рекомендую вам с ней ознакомиться — это поможет лучше понять, о чём будет говориться далее.
Введение
С появлением глубокого обучения “компьютерное зрение” перешло на новую ступень развития. На смену разрозненным значениям пикселей и ограниченному количеству созданных вручную признаков пришли способы сделать машинное распознавание деталей изображения более простым и понятным — это привело к смене парадигмы в этой области. Сегодня в привычных нам вещах из сфер производства и торговли используется множество самых современных приложений для компьютерного зрения. Недавний прорыв в сфере глубокого обучения в компьютерном зрении привнёс колоссальные изменения в нашу повседневную жизнь. Вы могли даже не заметить, как именно в каких-то вещах используется компьютерное зрение. Вот несколько любопытных примеров: автопилот в автомобилях Tesla, разблокировка с помощью Face ID, Animoji и продвинутый функционал камеры в iPhone, эффект боке в режиме портретной съёмки, фильтры в мессенджерах Snapchat и Facebook и т. д.
Основная идея компьютерного зрения начинается с очень простой задачи — определить, что изображено на картинке. Оказывается, эту задачу чрезвычайно сложно решить, хотя мы, люди, легко справляемся с ней.
В цифровом формате изображения представлены в виде 3D-матрицы из значений пикселей (длины, ширины и цветовых каналов RGB). Извлекать информацию из этой 3D-матрицы не так уж просто.
Немного истории
Устаревшие решения для компьютерного зрения
С появлением машинного обучения проблемы компьютерного зрения решались относительно успешно. Прежде всего, в этом помогали созданные вручную признаки и традиционные алгоритмы машинного обучения, такие как метод опорных векторов (SVM). Созданные вручную признаки — это параметры изображений, извлекаемые с помощью множества других алгоритмов. Типичный пример — поиск контуров и углов. Простой алгоритм контурного детектора ищет области резкого изменения насыщенности изображения, то есть большую разницу в значениях соседних пикселей. Несколько таких вот простых и пара более сложных признаков выделялись с помощью комбинации алгоритмов и далее передавались алгоритму контролируемого машинного обучения.
Такой подход работает, однако результаты не особо впечатляют. Прежде всего, чтобы создать признаки самостоятельно, придётся приложить немало усилий, скажу больше — это требует серьёзного уровня предметных знаний. К тому же признаки сильно отличаются от случая к случаю. К примеру, то, что создано для диагностики переломов на рентгеновских снимках, вполне может не подойти для распознавания имени на почтовой посылке.
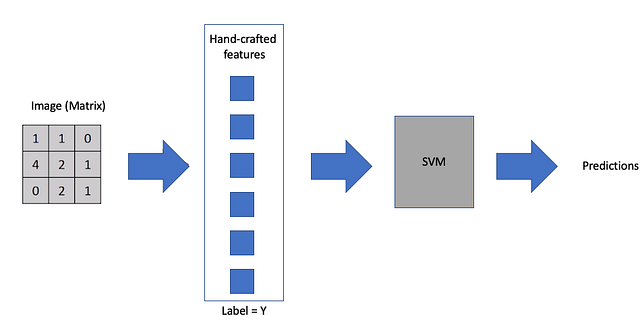
Image (Matrix) - Изображение (Матрица)
Hand-crafted features - Созданные вручную признаки
Label - Метка
Predictions - ПрогнозыЧтобы упросить процесс создания признаков, мы можем представить изображение в табличной форме, то есть когда каждый пиксель преобразуется в признак. Однако результат неутешительный: не остаётся практически никакой информации, которую может использовать нейросеть/алгоритм МО — отсюда плохая производительность.
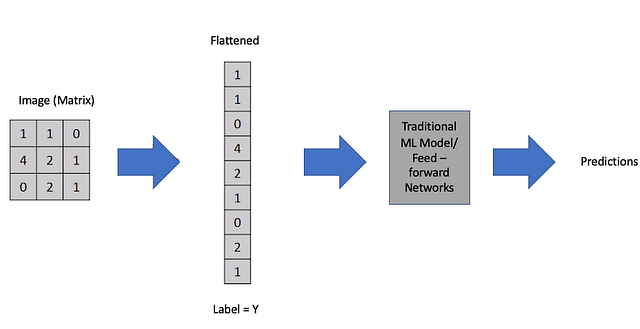
Image (Matrix) - Изображение (Матрица)
Flattened - Уплощённое (изображение)
Label - Метка
Traditional ML Model/Feed-Forward Networks - Традиционная модель МО/Нейросети прямого распространения
Predictions - ПрогнозыИз сказанного выше можно выделить важный момент: извлечение признаков из изображения — неизбежная, но трудно реализуемая необходимость.
Рассмотрим несколько примеров, чтобы понять, почему задачи, предполагающие использование компьютерного зрения, сложно решить. Для простоты давайте предположим, что наша бинарная задача — найти на картинке кошку.
Взгляните на два изображения ниже: если основываться на значениях пикселей, эти изображения имеют совершенно разное представление в цифровом формате. Поскольку в пикселе передаётся только его цвет, семантическое значение исходного представления неочевидно.

К тому же часто окрас кошки сливается с фоном. Посмотрите на изображения ниже: применение традиционных признаков оказалось бы безрезультатным. Таким образом, созданные вручную признаки здесь менее эффективны.

К тому же кошку можно сфотографировать во множестве совершенно разных поз, и это ещё больше усложняет процесс. Далее представлено всего несколько возможных вариантов.

При перенесении этих проблем на более общие случаи (к примеру, на поиск множества объектов на изображении) сложность возрастает экспоненциально.
Очевидно, что табличное представление пикселей, самостоятельное создание признаков для поиска конкретных параметров или сочетание двух этих подходов — не лучшие способы решать задачи, связанные с компьютерным зрением.
Есть ли лучшее решение?
Как показал опыт, созданные вручную признаки пусть и требуют много усилий, но всё же в некоторой степени способны решать стоящие перед ними задачи. Однако этот процесс получился бы крайне дорогостоящим, а для решения каждой отдельной задачи требовались бы обширные предметные знания.
Что если автоматизировать извлечение признаков?
К счастью, такое возможно, и это наконец подводит нас к нашей основной теме — свёрточным нейронным сетям. СНС предоставляют продвинутые способы решения задач компьютерного зрения с использованием универсального, масштабируемого, самодостаточного подхода, который можно применять к разным предметным областям без необходимости знать о них что-либо. Больше не требуется создавать признаки самим, поскольку нейросеть сама учится извлекать полезные признаки при достаточном обучении и объёме данных.
О глубоких свёрточных нейронных сетях впервые заговорили в своих публикациях Хинтон, Крижевский и Суцкевер. Тогда такие сети применялись, чтобы добиться высочайшей производительности в работе по классификации проекта ImageNet. Это исследование совершило революцию в сфере компьютерного зрения.
Подробнее о глубоких свёрточных нейросетях
Обобщённая архитектура СНС показана ниже. Некоторые детали пока могут казаться неясными, но подождите немного — скоро мы подробно разберём каждый компонент. Компонент извлечения (экстрактор) признаков в этой архитектуре — это комбинация свёртки и пулинга. Вероятно, вы заметили, что этот компонент повторяется — такое можно увидеть в большинстве современных архитектур. Эти экстракторы извлекают вначале низкоуровневые признаки (например, контуры и линии), затем среднеуровневые (формы и комбинации из нескольких низкоуровневых признаков) и, наконец, высокоуровневые признаки (ухо/нос/глаза в примере с распознаванием кошки). В конце эти слои уплощаются и связываются с выходным слоем функцией-активатором (как и в нейронных сетях прямого распространения).
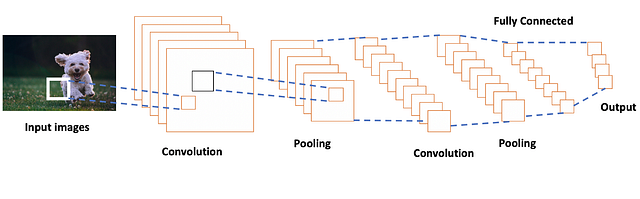
Input Images - Изображения на входе
Convolution - Свёртка
Pooling - Пулинг
Fully Connected - Полносвязный слой
Output - ВыходНачнём с основ
Давайте разберёмся, как человеческий мозг распознаёт образы с помощью зрения. Говоря простым языком, наш мозг принимает сигналы с сетчатки о полученных из внешнего мира визуальных образах. Сначала распознаются контуры, затем эти контуры помогают распознать изгибы, потом идут более сложные паттерны (например, форма) и т. д. Иерархическая организация нейронной активности от контуров до линий, изгибов и всё усложняющихся форм помогает идентифицировать конкретный объект. Конечно, это очень упрощённая интерпретация процесса, и человеческий мозг одновременно производит гораздо более сложные операции.
По аналогии с этим в свёрточных нейросетях изучение элементарных признаков происходит в первичных слоях. Слово “глубокий” в выражении “глубокие СНС” относится к количеству слоёв в сети. В обычной СНС, как правило, бывает 5–10 и даже больше слоёв по изучению признаков. Архитектуры самых современных приложений включают нейросети с более 50–100 слоями. Работа СНС схожа с упрощённой моделью работы человеческого мозга по распознаванию визуальных компонентов в зрительной коре.
Подробнее о структуре СНС
Начнём со свёртки.
“Свёртка” — операция из области обработки сигнала. В глубоком обучении это перемножение матрицы изображения (собственно матрица) и ядра/фильтра (ещё одна матрица меньшего размера) путём прохождения через длину и ширину. На анимации ниже демонстрируется свёртка фильтра/ядра размером 3×3 и изображения размером 5×5. Результат свёртки — изображение меньшего размера (3×3).
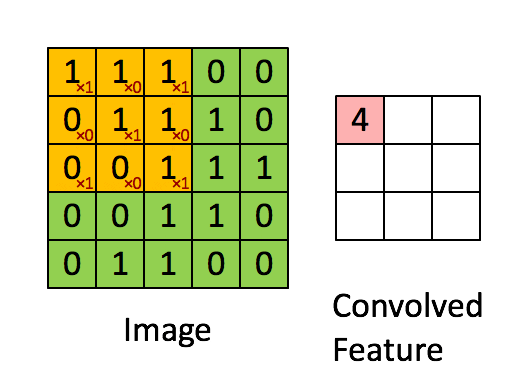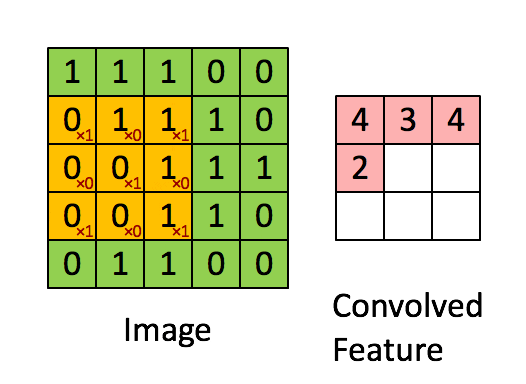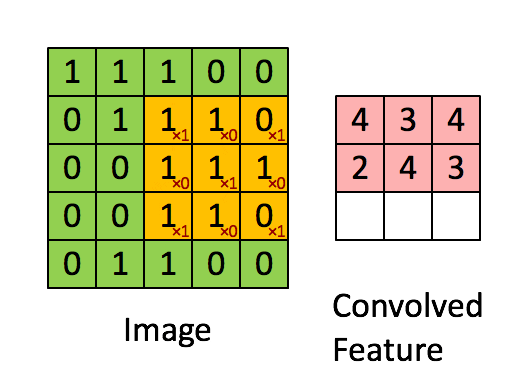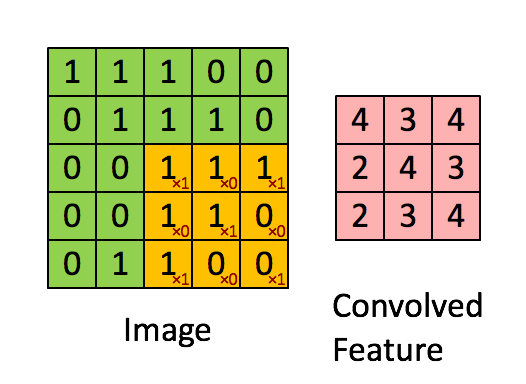
Image - Изображение
Convolved Feature - Признак-результат свёрткиЭто перемножение матриц по сути является основой извлечения признаков. Опираясь на верные значения в ядре, можно извлечь значимые признаки изображения. Пример применения такой манипуляции приведён ниже. Можно заметить, что оригинальное изображение не меняется, если использовать ядро в качестве матрицы тождественности. Однако при использовании разных ядер результат может напоминать применение других контурных детекторов и техник сглаживания или увеличения резкости изображения.

Это один аспект компонента. Другой его аспект — пулинг. Слой пулинга помогает сократить пространственное представление изображения, чтобы уменьшить количество параметров и объём вычислений в сети. Это простая операция: надо только задать максимальное значение определённому размеру ядра. Ниже дан простой пример пулинга: он проводится с использованием ядра размером 10×10 на выходе свёртки (другой матрицы) размером 20×20. В итоге получается матрица размером 2×2.
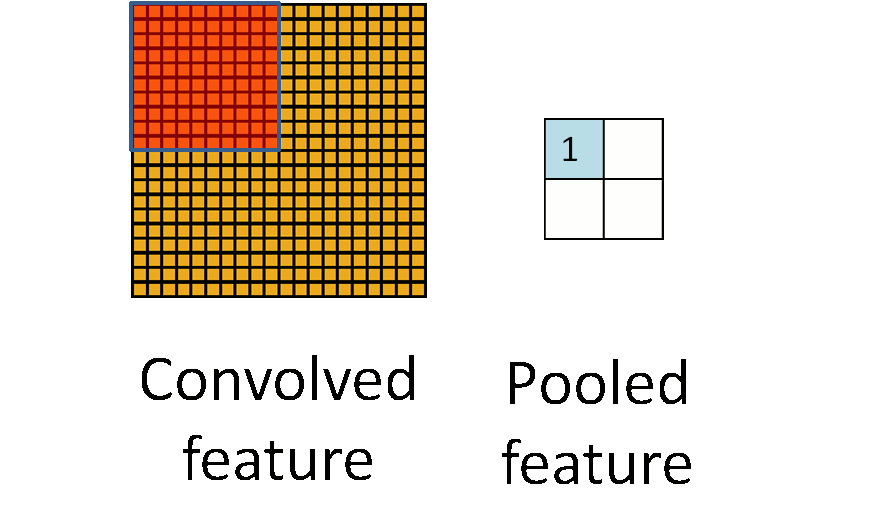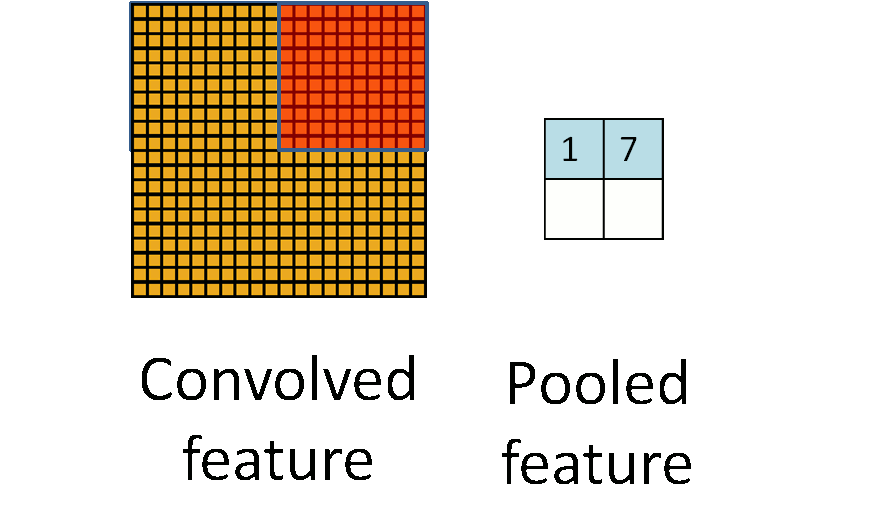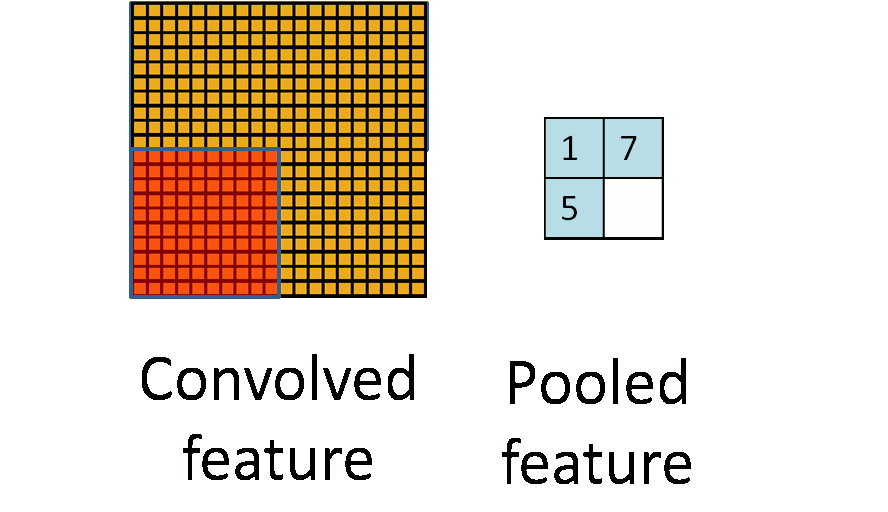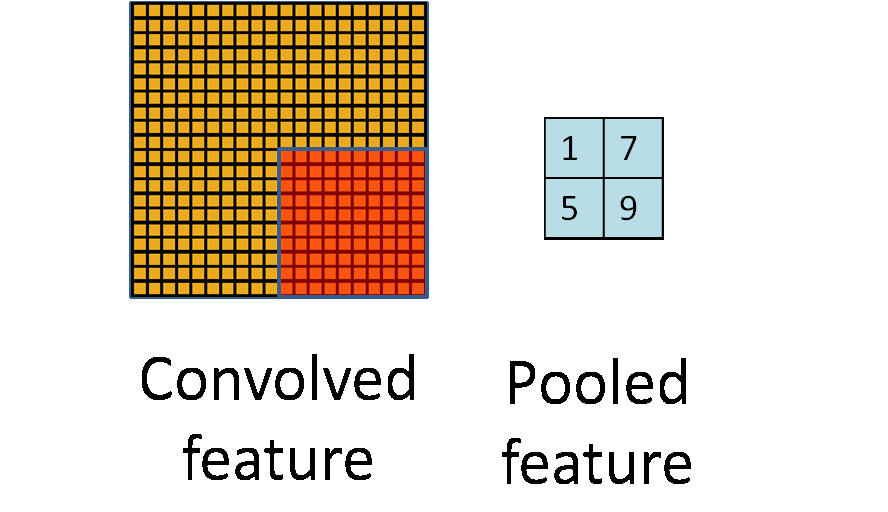
Convolved Feature - Признак-результат свёртки
Pooled Feature - Признак-результат пулингаИспользуя комбинацию слоёв свёртки и слоёв пулинга (с определением максимального значения), мы получаем основной структурный элемент СНС. Свёртка и пулинг уменьшают исходные размеры изображения на входе в зависимости от размеров ядра и пулинга. Применяя свёртку с одним ядром, получаем карту признаков. В СНС обычно применяется несколько ядер на одну свёртку. На рисунке ниже показаны карты признаков, извлечённых из n ядер при свёртке.
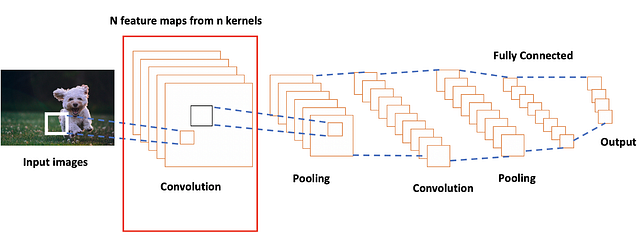
N feature maps from n kernels - N карт признаков из n ядер
(Перевод остальных понятий - в комментарии к рисунку 3)Многократное повторение этого процесса приводит к углублению свёрточных нейронных сетей. Каждый слой извлекает признаки из предыдущего. Иерархическая организация слоёв способствует последовательному изучению признаков: от контуров к более сложным признакам, созданным из простых, и далее к высокоуровневым признакам, которые уже содержат достаточно информации для составления нейросетью точного прогноза.
Последний свёрточный слой связан с полносвязным слоем, который используется для применения подходящей функции-активатора для прогнозирования выхода: для бинарных выходов используется сигмоидная, а для небинарных — многопеременная функция.
Вся описанная архитектура в упрощённом виде показана ниже.
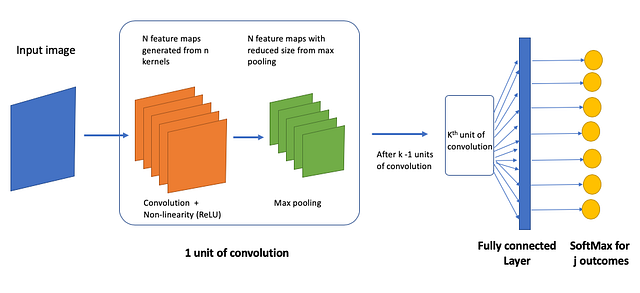
Input Image - Изображение на входе
N feature maps generated from n kernels - N карт признаков, сгенерированных из n ядер
Convolution + Non-linearity (ReLU) - Свёртка + Нелинейность (Блок линейной ректификации)
N feature maps with reduced size from max pooling - N карт признаков с уменьшенным размером из-за применения пулинга с определением максимального значения
Max Pooling - Пулинг с определением максимального значения
1 unit of convolution - Один сегмент свёртки
After k-1 units of convolution - Сегменты свёртки после первого ядра
Kth unit of convolution - Сегмент свёртки с порядковым номером K
Fully Connected Layer - Полносвязный слой
SoftMax for j outcomes - Применение многопеременной функции активации к выходам в количестве jДо сих пор мы не уделяли внимание нескольким важным аспектам сложной архитектуры СНС. Я сделал это специально, чтобы не усложнять и помочь вам разобраться с основами структурных элементов СНС.
Вот ещё пара ключевых понятий:
- Шаг (страйд). Говоря простыми словами, шаг — это количество сегментов, по которым одновременно проходится фильтр. Когда мы говорили об обработке фильтром входного изображения, то полагали, что шаг фильтра равен 1 сегменту в заданном направлении. Мы можем сами регулировать количество сегментов (хотя обычно используется 1). В зависимости от условий конкретного случая можно выбрать более подходящее значение шага. Более широкие шаги обычно помогают уменьшать объём вычислений, обобщать результаты изучения признаков и т. д.
- Дополнение. Мы также видели, что применение свёртки уменьшает размер карты признаков по сравнению с размером входного изображения. Дополнение нулями — обычный способ контролировать степень сжатия после применения фильтров, размеры которых превышают 1×1, чтобы избежать потерь информации на границах изображения.
Две иллюстрации ниже отлично демонстрируют понятия дополнения и шага.
- Дополнение без шагов (голубым показан вход, зелёным — выход):
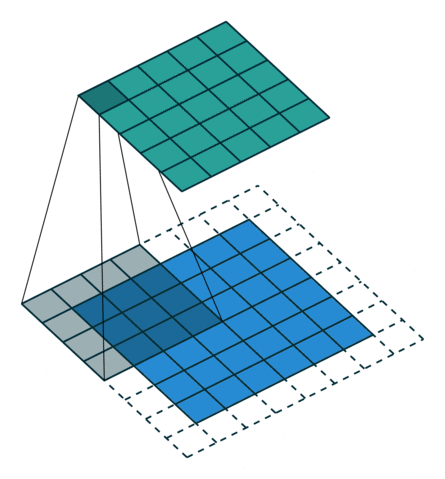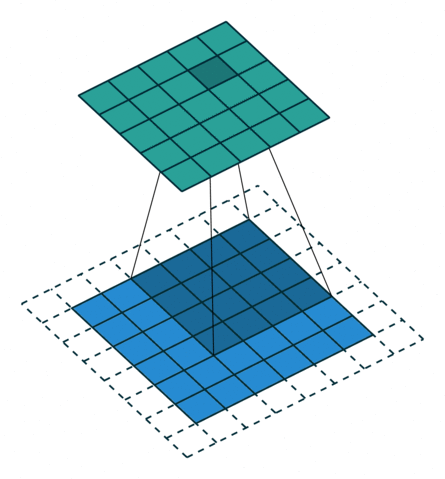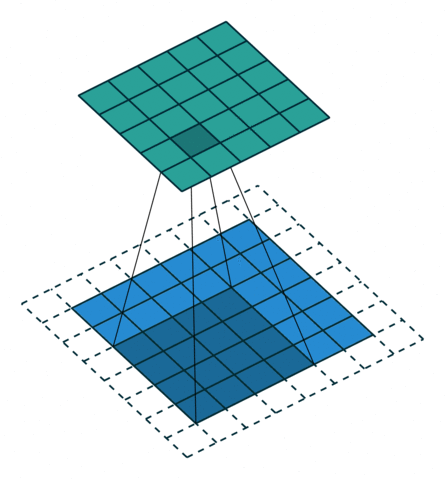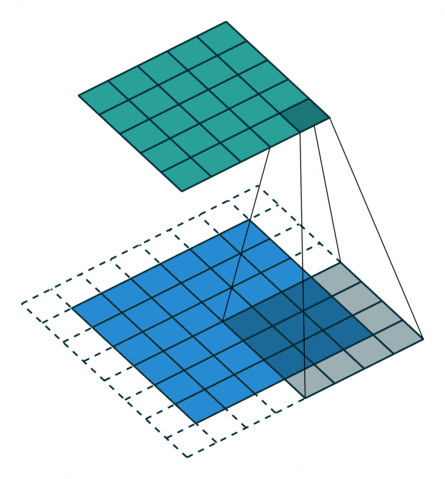
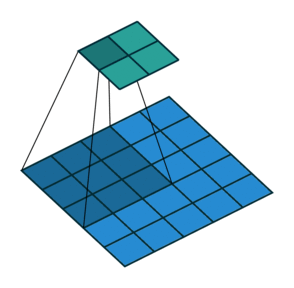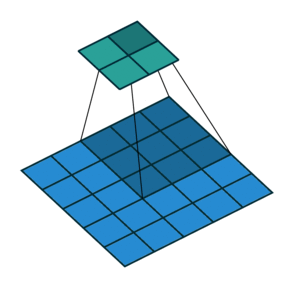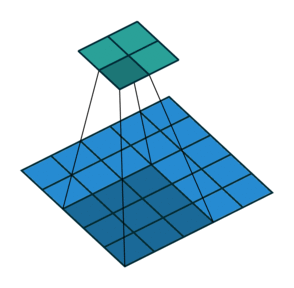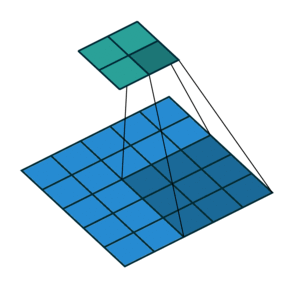
2. Шаги без дополнения (голубым показан вход, зелёным — выход):
Есть ещё пара важных аспектов, которых мы пока не касались — слои пакетной нормализации и слои исключения. Оба эти понятия значимы и важны для СНС. Сегодня мы определяем сегмент свёртки как комбинацию трёх компонентов (свёртка + пулинг с определением максимального значения + пакетная нормализация), а не двух первых. Пакетная нормализация — это приём, который помогает упростить обучение очень глубоких нейронных сетей путём стандартизации входов в слой для каждого мини-пакета. Стандартизация входов стабилизирует процесс обучения и таким образом уменьшает количество эпох обучения глубоких нейросетей.
В свою очередь исключение — это приём регуляризации, который отлично справляется с переобучением и чрезмерным обобщением.
Связываем всё воедино
Теперь, когда мы уже неплохо разбираемся в основных структурных элементах свёрточной нейронной сети, уверен, у вас появились более детальные вопросы. Самые важные, которые могли возникнуть, касаются фильтров: “Как решить, какие фильтры использовать?”, “Сколько фильтров использовать?” и т. п.
Давайте отдельно ответим на каждый из этих вопросов.
Как решить, какие фильтры использовать?
Ответ на этот вопрос простой. Мы устанавливаем фильтры со случайными значениями на основе нормального или какого-либо другого распределения. Эта идея может казаться немного неоднозначной и трудной для понимания, однако она хорошо работает. В процессе обучения нейронная сеть постепенно изучает лучшие фильтры, которые помогают извлекать максимум информации, необходимой для точного прогноза метки. Здесь-то и случается магия: мы, строго говоря, избавляемся от необходимости создавать признаки самостоятельно. При достаточном обучении и объёме данных нейросеть сама создаёт подходящие фильтры для извлечения наиболее значимых признаков.
Сколько фильтров использовать в каждом сегменте свёртки?
Здесь нет никаких стандартов. Размер и количество фильтров — настраиваемые гиперпараметры. Универсальное правило — использовать фильтры с нечётными размерами (3×3, 5×5, 7×7). Также крупным фильтрам обычно предпочитают маленькие, но возможны и компромиссные соотношения, которые надо вычислять эмпирически.
Как обучается сеть?
Процесс похож на обучение нейросетей прямого распространения, которые мы обсуждали в предыдущей статье. Мы используем алгоритм обратного распространения ошибки, для того чтобы сеть меняла веса фильтров и изучала основные признаки изображения. Обучение позволяет нейросети находить оптимальные фильтры для извлечения максимального объёма информации из изображений на входе.
Изображение выше было обычным 2D, в то время как большинство изображений представляют собой 3D. Как нейросеть работает с 3D?
2D-изображения демонстрировались для простоты. Большинство используемых изображений — 3D с цветовыми каналами (RGB). В этом случае ничего не меняется, кроме измерений ядра. Ядра будут трёхмерными, где третье измерение равно количеству каналов: например, 5x5x3 для 3 цветовых каналов (R, G и B) в изображении на входе.
Какая разница между свёрточными нейронными сетями и глубокими свёрточными нейронными сетями?
Это одно и то же. Слово “глубокий” здесь относится к количеству слоёв в архитектуре. Большинство современных СНС содержит от 30 до 100 слоёв.
Нужны ли для обучения СНС графические процессоры (GPU)?
Не обязательны, но желательны. Эффективное использование GPU позволяет увеличить скорость обработки изображений при обучении нейросетей примерно в 50 раз. Платформы Kaggle и Google Colab предоставляют бесплатные (с ограниченной частотой использования в неделю) окружения с поддержкой GPU.
Заканчиваем с основами — впереди реальный пример
Давайте на практике разберём пример, который демонстрирует создание свёрточной нейронной сети при помощи библиотеки PyTorch.
Здесь нам пригодится всё вышеизложенное.
Для начала давайте импортируем все необходимые пакеты: утилиты, модули ядер нейронной сети и несколько внешних модулей из библиотеки Scikit-learn для оценки производительности нейросети.
#импорт утилит pytorch
import torch
from torch.utils.data import DataLoader, TensorDataset
#импорт нейронной сети
import torch.nn as nn, torch.nn.functional as F, torch.optim as optim
from torch.autograd import Variable
#импорт внешних библиотек
import pandas as pd,numpy as np,matplotlib.pyplot as plt, os
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, accuracy_score
%matplotlib inline
#установка устройства на GPU или CPU (в зависимости от их наличия)
if torch.cuda.is_available():
device = torch.device('cuda')
else:
device = torch.device('cpu')Далее загружаем набор данных из памяти. К примеру, я использую набор данных MNIST в csv-формате с Kaggle. Вы можете найти полный набор здесь.
input_folder_path = "../input/"
#Файл CSV представляет собой неструктурированный файл с изображениями размером 28*28. Каждое из них уплощено в ряд из 784 колонок (1 колонка = 1 значение пикселя)
#Для СНС нам нужно изменить эту форму на желаемую
train_df = pd.read_csv(input_folder_path+"train.csv")
#Первая колонка - это цель/метка
train_labels = train_df['label'].values
#Значения пикселей начинаются со второй колонки
train_images = (train_df.iloc[:,1:].values).astype('float32')
#Сплит обучения и проверки
train_images, val_images, train_labels, val_labels = train_test_split(train_images, train_labels,
stratify=train_labels, random_state=2020,
test_size=0.2)
#Преобразование плоского ряда в [#изображения,#Каналы,#Ширина,#Высота]
#Поскольку изображение в оттенках серого, то будет всего 1 канал
train_images = train_images.reshape(train_images.shape[0],1,28, 28)
val_images = val_images.reshape(val_images.shape[0],1,28, 28)
#Вывод нескольких образцов
for i in range(0, 6):
plt.subplot(160 + (i+1))
plt.imshow(train_images[i].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.title(train_labels[i])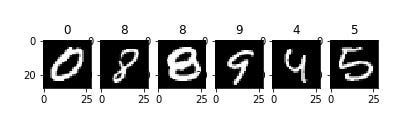
Теперь, когда мы загрузили данные, давайте преобразуем их в представление, понятное PyTorch.
#Конвертация изображений для обучения из массива pandas/numpy в многомерный массив и нормализация значений
train_images_tensor = torch.tensor(train_images)/255.0
train_images_tensor = train_images_tensor.view(-1,1,28,28)
train_labels_tensor = torch.tensor(train_labels)
#Создание TensorDataset для обучения
train_tensor = TensorDataset(train_images_tensor, train_labels_tensor)
#Конвертация изображений для проверки из массива pandas/numpy в многомерный массив и нормализация значений
val_images_tensor = torch.tensor(val_images)/255.0
val_images_tensor = val_images_tensor.view(-1,1,28,28)
val_labels_tensor = torch.tensor(val_labels)
#Создание TensorDataset для проверки
val_tensor = TensorDataset(val_images_tensor, val_labels_tensor)
print("Train Labels Shape:",train_labels_tensor.shape)
print("Train Images Shape:",train_images_tensor.shape)
print("Validation Labels Shape:",val_labels_tensor.shape)
print("Validation Images Shape:",val_images_tensor.shape)
#Загрузка TensorDataset для обучения и проверки в генератор данных для итераций обучения
train_loader = DataLoader(train_tensor, batch_size=64, num_workers=2, shuffle=True)
val_loader = DataLoader(val_tensor, batch_size=64, num_workers=2, shuffle=True)
Train Labels Shape - Форма меток для обучения
Train Images Shape - Форма изображений для обучения
Validation Labels Shape - Форма меток для проверки
Validation Images Shape - Форма изображений для проверкиНастало время определить архитектуру СНС, а также дополнительные функции, которые пригодятся при оценке и составлении прогнозов.
class ConvNet(nn.Module):
def __init__(self, num_classes=10):
super(ConvNet, self).__init__()
#Первый сегмент свёртки
self.conv_unit_1 = nn.Sequential(
nn.Conv2d(1, 16, kernel_size=3, stride=1, padding=1),
nn.BatchNorm2d(16),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2))
#Второй сегмент свёртки
self.conv_unit_2 = nn.Sequential(
nn.Conv2d(16, 32, kernel_size=3, stride=1, padding=1),
nn.BatchNorm2d(32),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2))
#Полносвязные слои
self.fc1 = nn.Linear(7*7*32, 128)
self.fc2 = nn.Linear(128, 10)
def forward(self, x):
out = self.conv_unit_1(x)
out = self.conv_unit_2(out)
out = out.view(out.size(0), -1)
out = self.fc1(out)
out = self.fc2(out)
out = F.log_softmax(out,dim=1)
return out
#Определение функций для оценки модели и составления прогнозов
def make_predictions(data_loader):
model.eval()
test_preds = torch.LongTensor()
actual = torch.LongTensor()
for data, target in data_loader:
if torch.cuda.is_available():
data = data.cuda()
output = model(data)
preds = output.cpu().data.max(1, keepdim=True)[1]
test_preds = torch.cat((test_preds, preds), dim=0)
actual = torch.cat((actual,target),dim=0)
return actual,test_preds
def evaluate(data_loader):
model.eval()
loss = 0
correct = 0
for data, target in data_loader:
if torch.cuda.is_available():
data = data.cuda()
target = target.cuda()
output = model(data)
loss += F.cross_entropy(output, target, size_average=False).data.item()
predicted = output.data.max(1, keepdim=True)[1]
correct += (target.reshape(-1,1) == predicted.reshape(-1,1)).float().sum()
loss /= len(data_loader.dataset)
print('\nAverage Val Loss: {:.4f}, Val Accuracy: {}/{} ({:.3f}%)\n'.format(
loss, correct, len(data_loader.dataset),
100. * correct / len(data_loader.dataset)))
#Создание модели
model = ConvNet(10).to(device)
#Определение потерь и оптимизатора
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
print(model)
И, наконец, давайте обучим модель.
num_epochs = 5
# Обучение модели
total_step = len(train_loader)
for epoch in range(num_epochs):
for i, (images, labels) in enumerate(train_loader):
images = images.to(device)
labels = labels.to(device)
# Дальнейшая передача
outputs = model(images)
loss = criterion(outputs, labels)
# Обращение и оптимизация
optimizer.zero_grad()
loss.backward()
optimizer.step()
#Вывод потерь обучения и потерь проверки + точности после каждой эпохи
print ('Epoch [{}/{}], Loss: {:.4f}' .format(epoch+1, num_epochs, loss.item()))
evaluate(val_loader)
Epoch - Эпоха
Loss - Потери
Average Val Loss - Среднее значение потерь при проверке
Val Accuracy - Точность проверкиТеперь у нас есть простая модель с периодом обучения в 5 эпох. В большинстве случаев для достижения отличной производительности требуется более 30 эпох. Давайте посчитаем точность в наборе данных для проверки и построим матрицу неточностей.
#Составление прогнозов по набору данных для проверки
actual, predicted = make_predictions(val_loader)
actual,predicted = np.array(actual).reshape(-1,1),np.array(predicted).reshape(-1,1)
print("Validation Accuracy-",round(accuracy_score(actual,predicted),4)*100)
print("\n Confusion Matrix\n",confusion_matrix(actual,predicted))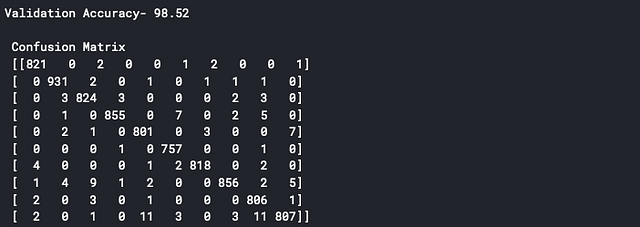
Validation Accuracy - Точность проверки
Confusion Matrix - Матрица неточностейНа этом мы заканчиваем наше поверхностное знакомство с этой сложной темой. Надеюсь, вам понравилось. Также рекомендую попрактиковаться с этим замечательным инструментом, чтобы понимать, как каждый слой генерирует фильтры и карты признаков для разных входных изображений.
Вы также можете загрузить всю памятку целиком с моего репозитория — PyTorchExamples.
Заключение
Целью этой статьи было познакомить новичков с основами темы, используя простые объяснения. Упрощение расчётов и сосредоточение на функционале позволит эффективно использовать глубокие свёрточные нейросети для современных корпоративных проектов.
Читайте также:
- Как сгенерировать настоящие случайные числа в Solidity с блокчейном
- 7 способов раскрыть жульничество аналитика данных
- Что такое тензор?
Перевод статьи Jojo John Moolayil: A Layman’s Guide to Deep Convolutional Neural Networks






