Теория сетей
Начнем с краткого введения в базовые компоненты сети: узлы и ребра.
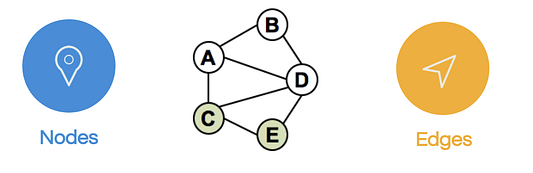
- Узлы (например, A,B,C,D,E) обычно представляют объекты в сети и содержат собственные и сетевые свойства. К собственным относятся вес, размер, расположение и прочие атрибуты, а к сетевым — количество соседей (степень) и связная компонента, которой принадлежит узел (кластер).
- Ребра — это связи между узлами, которые в некоторых случаях также содержат свойства. Например, вес, который определяет силу соединения, направление при ассиметричном отношении, а также время.
Эти два базовых элемента способны описывать множество явлений: социальные связи, виртуальную сеть маршрутизации, физические электросети, дорожную сеть, сети биологических связей и прочие отношения.
Реальные сети
Реальные и, в частности, социальные сети обладают уникальной структурой, которая обычно отличает их от случайных математических сетей.
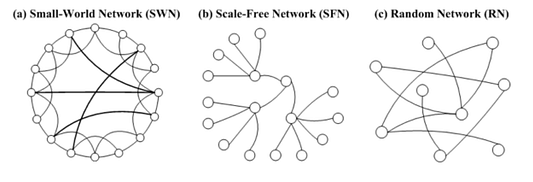
- Согласно феномену “Мир тесен”, в реальных сетях пути между подключенными участниками часто очень коротки. Это применимо как к реальным и виртуальным социальным сетям (теория шести рукопожатий), так и к физическим, например аэропортам и электричеству маршрутизации трафика.
- Безмасштабные сети со степенным законом распределения (power-law) обладают асимметричной популяцией с несколькими сильно связанными узлами (например, социальное влияние) и множеством слабо связанных узлов.
- Гомофилия — склонность людей образовывать связи с подобными себе, что приводит к схожести свойств между соседями.
Меры центральности
Централизованные узлы играют ключевую роль в сети, выступая в качестве центров для различных тенденций. Определение и значимость центральности могут различаться от случая к случаю и ссылаться на различные показатели. Примеры указаны ниже.
- Степень (Degree) — количество соседей узла.
- Влиятельность (EigenVector/PageRank) — итеративные циклы соседей.
- Близость (Closeness) — степень близости ко всем узлам.
- Посредничество (Betweenness) — количество коротких путей, проходящих через узел.
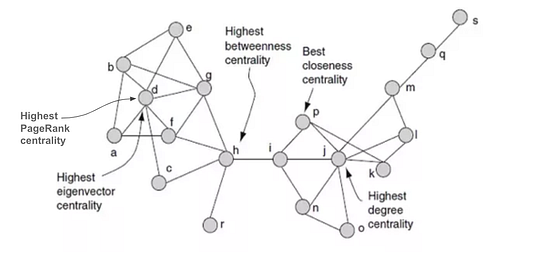
Меры варьируются в зависимости от сценария: ранжирование (page-rank), обнаружение критических точек (betweenness), транспортные узлы (closeness) и прочие.
Построение сети
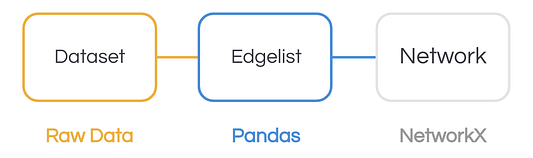
Для построения сетей подойдет любой набор данных, в котором можно описать связи между узлами. В данном примере мы построим и визуализируем сеть голосования для Евровидения 2018 на основе официальных данных. Для этого воспользуемся пакетом Python Networkx.
Мы прочитаем данные из файла Excel в датафрейм Pandas, чтобы получить табличное представление голосов. Каждая строка включает все голоса из определенной страны. Мы распределим набор так, чтобы в каждой из них был представлен один голос (ребро) между двумя странами (узлы).
Затем построим ориентированный граф с помощью Networkx из edgelist, с которым мы работаем в формате датафрейма Pandas. И наконец, для визуализации мы применим метод обобщения, как показано во фрагменте кода ниже.
votes_data = pd.read_excel('ESC2018_GF.xlsx',sheetname='Combined result')
votes_melted = votes_data.melt(
['Rank','Running order','Country','Total'],
var_name = 'Source Country',value_name='points')
G = nx.from_pandas_edgelist(votes_melted,
source='Source Country',
target='Country',
edge_attr='points',
create_using=nx.DiGraph())
nx.draw_networkx(G)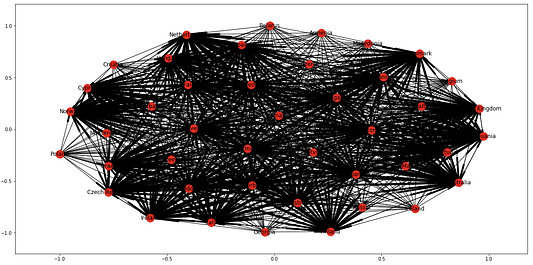
Визуализация
Встроенный метод draw выдает очень непонятную фигуру. Он пытается построить сильно связный граф, но без полезных “подсказок” полезную информацию из данных извлечь не получится. Мы улучшим фигуру, разделяя и охватывая различные визуальные аспекты с помощью предварительной информации об этих сущностях.
- Позиция (Position) — каждая страна присваивается в соответствии с географическим положением.
- Стиль (Style) — каждая страна распознается по флагу и его цветам.
- Размер (Size) — размер узлов и ребер представляет количество точек.
Теперь построим компоненты сети по частям.
countries = pd.read_csv('countries.csv',index_col='Country')
pos_geo = { node:
( max(-10,min(countries.loc[node]['longitude'],55)), # Определение масштаба
max(countries.loc[node]['latitude'],25)) #Определение масштаба
for node in G.nodes() }
pos_geo = {}
for node in G.nodes():
pos_geo[node] = (
max(-10,min(countries.loc[node]['longitude'],55)), # Определение масштаба
max(countries.loc[node]['latitude'],25) #Определение масштаба )
flags = {}
flag_color = {}
for node in tqdm.tqdm_notebook(G.nodes()):
flags[node] = 'flags/'+(countries.loc[node]['cc3']).lower().replace(' ','')+'.png'
flag_color[node] = ColorThief(flags[node]).get_color(quality=1)
def RGB(red,green,blue):
return '#%02x%02x%02x' % (red,green,blue)
ax=plt.gca()
fig=plt.gcf()
plt.axis('off')
plt.title('Eurovision 2018 Final Votes',fontsize = 24)
trans = ax.transData.transform
trans2 = fig.transFigure.inverted().transform
tick_params = {'top':'off', 'bottom':'off', 'left':'off', 'right':'off',
'labelleft':'off', 'labelbottom':'off'} #flag grid params
styles = ['dotted','dashdot','dashed','solid'] # line styles
pos = pos_geo
# Построение ребер
for e in G.edges(data=True):
width = e[2]['points']/24 #normalize by max points
style=styles[int(width*3)]
if width>0.3: #filter small votes
nx.draw_networkx_edges(G,pos,edgelist=[e],width=width, style=style, edge_color = RGB(*flag_color[e[0]]) )
# in networkx versions >2.1 arrowheads can be adjusted
# Построение узлов
for node in G.nodes():
imsize = max((0.3*G.in_degree(node,weight='points')
/max(dict(G.in_degree(weight='points')).values()))**2,0.03)
# Размер пропорционален голосам
flag = mpl.image.imread(flags[node])
(x,y) = pos[node]
xx,yy = trans((x,y)) # Координаты фигуры
xa,ya = trans2((xx,yy)) # Координаты осей
country = plt.axes([xa-imsize/2.0,ya-imsize/2.0, imsize, imsize ])
country.imshow(flag)
country.set_aspect('equal')
country.tick_params(**tick_params)
fig.savefig('images/eurovision2018_map.png')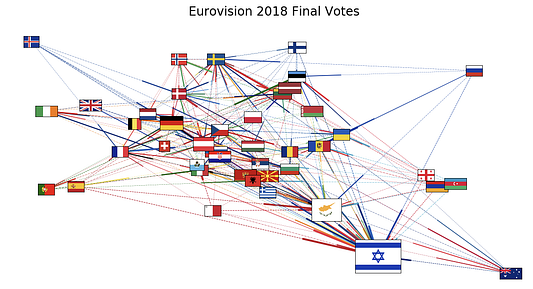
Новая фигура лучше читается и предоставляет краткий обзор голосов. В качестве общего примечания стоит добавить, что построение сетей — как правило, нелегкий процесс, требующий внимательно выбирать компромиссы между количеством представленных данных и передаваемым сообщением. Вы также можете попробовать другие инструменты визуализации сетей, например Gephi , Pyvis и GraphChi.
Поток информации
Для описания этого процесса распространения информации часто используются две популярные базовые модели.
Линейный порог определяет поведение, при котором влияние накапливается от нескольких соседей узла и активируется, только если превышает определенный порог. Такое поведение типично для рекомендаций фильмов: совет от одного из друзей может в конечном счете убедить человека посмотреть кино, если он услышит его и от нескольких других людей.
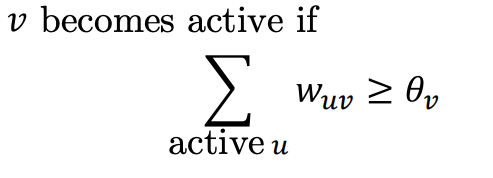
В модели независимых каскадов каждый из активных соседей узла может потенциально и независимо активировать его. Этот процесс напоминает распространение вирусной инфекции: каждое социальное взаимодействие может привести к заражению.
Пример потока информации
Чтобы проиллюстрировать процесс распространения информации, воспользуемся сетью “Буря мечей”, основанной на персонажах сериала “Игра престолов”. Сеть сконструирована на совместных появлениях героев в книге “Песнь льда и огня”.

Опираясь на модель независимых каскадов, мы попытаемся отследить динамику распространения слухов, которые часто встречаются в этом сериале.
Внимание, спойлер! Предположим, что в самом начале Джон Сноу ни о чем не знает, а двое его верных друзей Бран Старк и Сэмвел Тарли владеют очень важным секретом о его жизни. Посмотрим, как распространяются слухи по модели независимых каскадов.
def independent_cascade(G,t,infection_times):
# Выполнение шага t->t+1 в симуляции independent_cascade
# Каждый инфекционный узел заражает соседей с пропорциональной весу вероятностью
max_weight = max([e[2]['weight'] for e in G.edges(data=True)])
current_infectious = [n for n in infection_times if infection_times[n]==t]
for n in current_infectious:
for v in G.neighbors(n):
if v not in infection_times:
if G.get_edge_data(n,v)['weight'] >= np.random.random()*max_weight:
infection_times[v] = t+1
return infection_times
infection_times = {'Bran-Stark':-1,'Samwell-Tarly':-1,'Jon-Snow':0}
for t in range(10):
plot_G(subG,pos,infection_times,t)
infection_times = independent_cascade(subG,t,infection_times)Слух достигает Джона в точке t=1, распространяется на его соседей, а затем и по всей сети, получая широкую огласку.
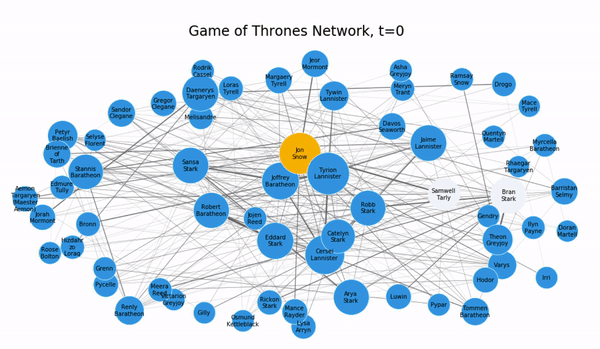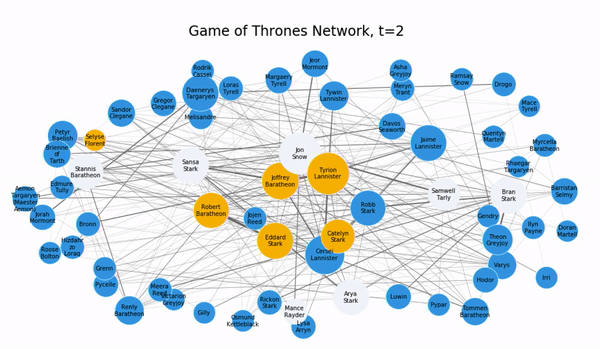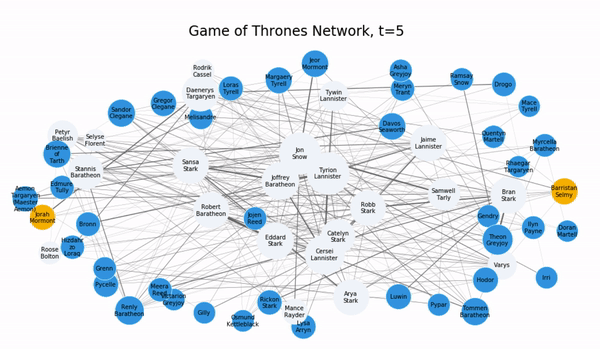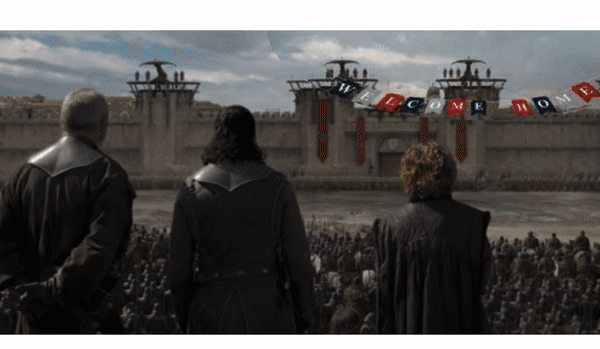
Динамика во многом зависит от параметров модели, которые влияют на закономерность процесса распространения.
Максимизация влияния
Проблема максимизации влияния описывает маркетинговую (и не только) установку, при которой цель маркетолога состоит в том, чтобы выбрать ограниченный набор узлов в сети, который будет естественным образом распространять влияние как можно большему количеству узлов. Например, пригласить на мероприятие по запуску продукта определенное число влиятельных лиц, которые затем расскажут о нем остальным участникам своей сети.
Подобных инфлюенсеров можно определить различными методиками, такими как меры центральности, упомянутыми выше. Вот самые центральные узлы в сети “Игра престолов”.
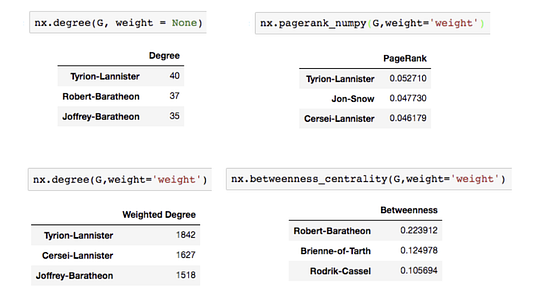
Как видите, некоторые персонажи повторно появляются на верхних позициях различных параметров. В сериале они также хорошо известны своим социальным влиянием.
Мы видим, что выбор одного узла может покрыть около 50% сети. Вот насколько важными могут быть социальные инфлюенсеры.
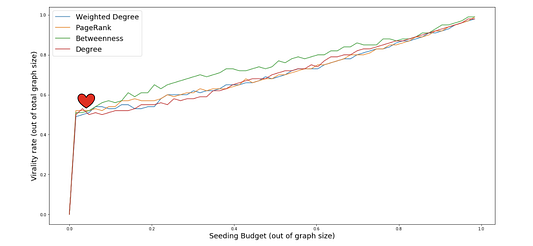
Однако максимизация влияния — нелегкий процесс и считается NP-трудной задачей. Чтобы найти лучший начальный набор для эффективного расчета, было разработано множество алгоритмов. Мы использовали метод полного перебора, чтобы выбрать лучшую начальную пару узлов (Роберт Баратеон и Кхал Дрого) в нашей сети. Процесс занял 41 минуту, и нам удалось достичь 56% покрытия. Получить такой результат с помощью алгоритмов центральности было бы непросто.
Вывод
Анализ сетей — сложный, но полезный инструмент, который пригодится в различных областях, особенно в стремительно растущих социальных сетях. Он применяется в маркетинговой максимизации влияния, обнаружении мошенничества и системах рекомендаций. Для работы с наборами данных сетей существует множество инструментов и методик. Выбирать их стоит с учетом уникальных свойств сети.
Читайте также:
- Классы данных в Python и их ключевые особенности
- Создание простой нейронной сети на Python
- 7 библиотек Python для вашего первого проекта по науке о данных
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Dima Goldenberg: Social Network Analysis: From Graph Theory to Applications with Python






