Теорема и наивный классификатор Байеса
Наивный классификатор Байеса — это набор простых и эффективных алгоритмов машинного обучения для решения различных задач классификации и регрессии. Эта статья может стать хорошим 5-минутным введением для тех, кто пропускал занятия по статистике, кому при слове «байесовский» становится некомфортно. На примере расчета вероятности посещения фитнес-зала я собираюсь в течение 5 минут объяснить теорему Байеса, а затем и алгоритм наивного классификатора Байеса. Кроме того, в моем GitHub есть пример простого кода на Python с использованием Scikit-learn. Итак, начинаем!
Краткое введение в теорему Байеса
Перед объяснением принципа работы алгоритма наивного классификатора Байеса, сначала следует разобраться с теоремой Байеса. В ее основе лежит условная вероятность (рис. 1). Фактически теорема Байеса — это всего лишь альтернативный или обратный способ вычисления условной вероятности (conditional probability). Когда сложно вычислить совместную вероятность P(A∩B) или легче вычислить обратную или байесовскую P(B | A), тогда можно применить теорему Байеса.
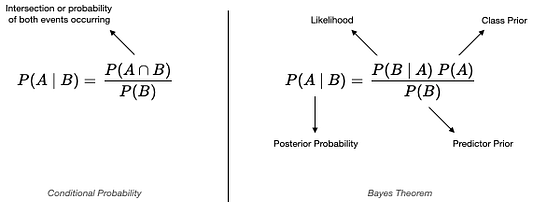
Теперь быстро определим отдельные термины из теоремы Байеса:
· Класс prior или априорная вероятность (prior probability): вероятность того, что событие А произойдет до того, как мы узнаем что-либо о событии В.
· Предварительный прогноз (Predictor prior) или обоснование: то же, что и предыдущий класс, но для события B.
· Апостериорная вероятность (Posterior probability): вероятность события A после получения информации о событии B.
· Возможность (Likelihood): обратная апостериорная вероятность.
В чем разница между теоремой и наивным классификатором Байеса?
Какое все это имеет отношение к наивному классификатору Байеса? Следует понимать, что различие между теоремой Байеса и наивным классификатором Байеса состоит в том, что наивный классификатор предполагает условную независимость, тогда как теорема Байеса ее не предполагает. Это означает, что между всеми входными свойствами классификатора нет взаимозависимости.
Возможно это не очень удачное предположение, но именно поэтому этот алгоритм называют «наивным» (naive). В этом также одна из причин ускоренной работы алгоритма. Несмотря на то, что алгоритм «наивен», он все же может превзойти сложные модели. Поэтому не позволяйте названию вводить вас в заблуждение.
Далее рассмотрим разницу в обозначениях между теоремой и наивным классификатором Байеса. Но сначала обратимся к одному из примеров использования теоремы Байеса, касающегося посещения тренажерного зала.
Пошаговое применение теоремы Байеса
Далее приведен простой пример, применимый для решения подобных задач. Администрация хочет получить прогноз посещаемости тренажерного зала с учетом погодных условий: P (присутствие = да | погода).
Шаг 1. Оценка ситуации или сбор исходных данных
У нас есть данные, где каждая строка представляет собой посещаемость тренажерного зала с учетом погоды. Так, наблюдение 3 — это участник, который посещал тренажерный зал в пасмурную погоду.
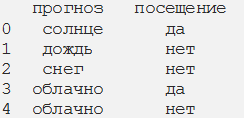
Шаг 2. Преобразуем набор данных в таблицу частотности
При этом мы получим суммарную посещаемость, исходя из погодных условий.
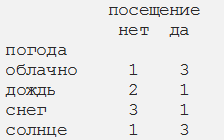
Шаг 3. Суммирование по строкам и столбцам для получения вероятностей

Если посмотреть на априорную вероятность класса (вероятность посещения), в среднем вероятность посещения тренажерного зала составляет 53%. К сведению, это типичное значение для большинства тренажерных залов: часто люди записываются, но ходят не регулярно. Однако задача заключается в получении вероятности посещения тренажерного зала с учетом погодных условий.
Шаг 5. Применение вероятностей из таблицы частотности к теореме Байеса
На рисунке 2 показана наша задача в представлении теоремы Байеса. Присвоим каждой из вероятностей на этом рисунке значение из приведенной выше таблицы частотности, а потом запишем уравнение так, чтобы оно стало более понятным.
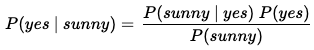
Возможность (Likelihood): P (солнце | да) = 3/8 или 0,375 (общее количество солнца И да, деленное на общее количество да)
Априорная вероятность класса: P (да) = 8/15 или 0,533
Априорная вероятность предиктора:P(солнце) = 4/15 или 0,267
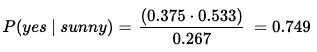
Согласно рисунку 3, любой участник посещает спортзал с вероятностью 75%, если будет солнечная погода. Это значение превышает среднюю посещаемость 53%! С другой стороны, вероятность посещения тренажерного зала в снежную погоду составляет всего 25% (0,125 ⋅ 0,533 / 0,267).
Поскольку этот пример из двоичной логики (посещать или не посещать), а P (да | солнечно) = 0,75 или 75 %, то обратное значение P (нет | солнечно) равно 0,25 или 25 %, так как сумма вероятностей должна составлять 1 или 100 %.
Вот так следует использовать теорему Байеса, чтобы найти апостериорную вероятность для систематизации. Алгоритм наивного классификатора Байеса похож на показанный далее пример. Следует обратить внимание на одну очевидную проблему в этом примере. Она заключается в том, что для погодных условий мы применяем одинаковую вероятность ко всем участникам, что не совсем логично. Но это был просто занимательный пример. Теперь обсудим дополнительные свойства и использование наивного классификатора Байеса.
Использование наивного классификатора Байеса с множеством свойств
Почти во всех случаях у вас в модели будет несколько свойств (features). Примерами свойств для тренажерного зала могут быть: возраст, тип членства, пол и т. д. Рассмотрим, как включить эти свойства в теорему и в наивный классификатор Байеса.
На рисунке 4 показана теорема Байеса, упрощенная до наивного алгоритма Байеса, включающего несколько свойств. В теореме Байеса вы должны вычислить единую условную вероятность с учетом всех свойств (вверху). С помощью наивного классификатора Байеса мы все упрощаем, вычисляя для каждого свойства условную вероятность, а затем перемножая их. Именно поэтому он и называется «наивным», поскольку условные вероятности всех свойств вычисляются независимо друг от друга. Алгоритм наивного классификатора Байеса серьезно упрощается за счет независимости и отбрасывания знаменателя. Вы можете повторить описанные выше шаги из теоремы Байеса, чтобы применить эти, теперь уже простые вычисления и, следовательно, корреляцию между теоремой и наивным классификатором Байеса.
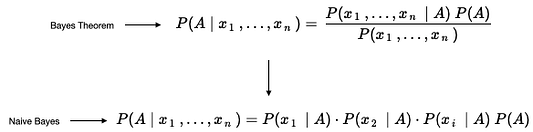
Заключение
В этом коротком 5-минутном введении в теорему и наивный классификатор Байеса использован пример с прогнозированием посещаемости тренажерного зала с помощью теоремы Байеса. Мы выяснили разницу между теоремой и наивным классификатором Байеса, показали упрощенные обозначения и объяснение “наивности” через предположение о независимости. К этому можно еще много чего добавить, но, надеюсь, что все изложенное дает базовое понимание теоремы и наивного алгоритма Байеса и позволит включать последний в ваши новые проекты.
Читайте также:
- 5 типов алгоритмов машинного обучения, которые нужно знать
- ML-инженер или специалист по обработке данных? (Закат науки о данных?)
- Разработка и развёртывание приложения машинного обучения: полное руководство
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Andre Violante: 5-Minute Machine Learning






