Возможно, вы помните теорему Байеса как громоздкое уравнение из курса статистики, которое вам нужно было заучить. Но за ним кроется нечто большее. Эта теорема лежит в основе альтернативного взгляда на статистику и вероятность, противостоящего мнению сторонников частотного подхода (или фреквентистов), и доброй половины величайших (или нуднейших) священных войн в академической среде.

Если вы проходили вводный курс статистики, то знакомы с частотным подходом (фреквентизмом), даже если и не слышали этого названия. В этом подходе параметры (математическое ожидание, дисперсия и т.д.) фиксированы, а данные случайны. Для сторонников частотного подхода вероятность — предел относительной частоты наблюдения некоторого события в серии однородных независимых испытаний.

Преподобный Томас Байес

У сторонников баейсовского подхода другой взгляд: параметры случайны, а данные фиксированы. Для них вероятность — это степень уверенности в том, что событие произойдёт. Кто же прав? Как это часто бывает, всё зависит от обстоятельств.

Чтобы продемонстрировать различные подходы, давайте рассмотрим, как оба лагеря подходят к простому вопросу: какова вероятность выпадения орла при подбрасывании монеты (назовём её P(H)).

Разумным частотным подходом будет подбросить монету достаточное число раз и вычислить P(H), используя метод максимального правдоподобия или метод моментов (в данном случае оба метода выглядят как отношение числа выпавших орлов к числу бросков монеты). Затем нужно построить приблизительный доверительный интервал и использовать его для вывода P(H). Совершенно разумный подход. 

Теперь давайте рассмотрим байесовский подход к той же задаче, который начинается с этого уравнения:

где θ— интересующий нас параметр, Y — случайная переменная (математическое ожидание), y — реализация случайной переменной (выборка), f_θ(θ) — априорное распределение, f_Y|θ(y|θ) — правдоподобие, f_θ|Y(θ|y) — апостериорное распределение, f_Y(y) — постоянная, которую можно проигнорировать

Априорное распределение — это уверенность в распределении интересующего параметра до изучения данных. Оно может быть основано на экспертном суждении или на неинформативном априорном распределении (априорное распределение, выражающее размытую или общую информацию о параметре). В нашем примере с монетой можно использовать функцию плотности вероятности бета-распределения в качестве общего распределения для P(H), потому что его значение находится между 0 и 1, как и значение вероятности. Мы должны указать параметры этого распределения, но пока оставим их не определёнными.

Правдоподобие — это наш шаблон. В примере с подбрасыванием монеты данные получаются из биномиального распределения, поэтому будем использовать функцию вероятности (число орлов за n бросков монеты соответствует биномиальному распределению).

Теперь мы готовы найти апостериорное распределение P(H), обозначенное греческой буквой θ.Число выпавших орлов обозначено Y (случайная переменная) и y (фактическое число выпадения орлов в выборке n).

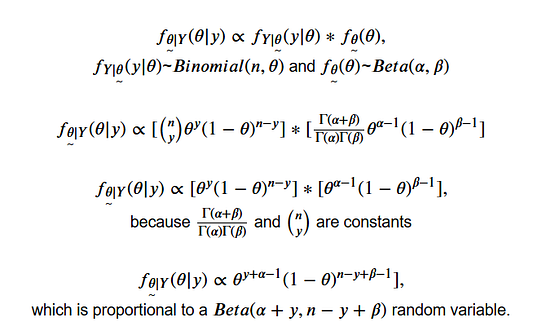
Решение апостериорного распределения биномиального правдоподобия с помощью априорного бета-распределения

Как видите, наше апостериорное убеждение P(H) основывается и на данных ( y и n), и на априорном убеждении P(H) (alpha и beta). При добавлении всё большего количества данных априорное убеждение всё меньше влияет на апостериорное. При достаточном количестве доказательств очень разные априорные распределения будут сходиться в одинаковое апостериорное. Сила априорного убеждения влияет на скорость схождения. 

Для демонстрации того, как доказательства перевешивают априорное распределение, я использовал Python, чтобы имитировать 100 бросков монеты и построить график апостериорного распределения для двух разных априорных распределений для 0, 10, 50 и 100 бросков (примечание: в этом примере параметр фиксирован, и байесовский анализ здесь не самая подходящая основа, но это простой пример). 

Для начала необходимо импортировать некоторые функции, задать число бросков монеты и P(H), а также задать параметры каждого априорного распределения:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta, bernoulli

# задаём число попыток
n = 100
# задаём вероятность выпадения орла
theta = 0.5

# априорное распределение смещения к выпадению орла
alpha1 = 5
beta1 = 2

# априорное распределение смещения к выпадению решки
alpha2 = 2
beta2 = 5

Теперь имитируем бросок монеты и подсчитаем значения после 10, 50 и 100 бросков.

# имитируем n бросков монеты с P(Heads) = theta
coin_flips = bernoulli.rvs(p=theta, size=n, random_state=1)

# считаем выпадение орла в первые 10 бросков
n_1 = 10
y_1 = sum(coin_flips[0:n_1])

# считаем выпадение орла в первые 50 бросков
n_2 = 50
y_2 = sum(coin_flips[0:n_2])

# считаем выпадение орла во всей выборке
y_total = sum(coin_flips)

Теперь определим функцию, чтобы создать апостериорное распределение, используя аналитически полученный результат.

def my_posterior(alpha_, beta_, n, y):
    # задаём диапазон theta (0 to 1) с шагом 100
    x = np.linspace(0, 1, 100)
    # вычисляем плотность вероятности для каждого события
    y = beta.pdf(x, (alpha_ + y), (n - y + beta_))
    # возвращаем x и апостериорную плотность вероятности
    return x, y

Наконец, мы готовы построить график апостериорного распределения для каждого априорного распределения после 0, 10, 50 и 100 бросков.

# строим график апостериорных распределений для beta (alpha1, beta1)
# априорных распределений
for i in [(0, 0), (n_1, y_1), (n_2, y_2),(n, y_total)]:
    label  = f"n = {i[0]}, y = {i[1]}"
    plt.plot(my_posterior(alpha1, beta1, i[0], i[1])[0],
             my_posterior(alpha1, beta1, i[0], i[1])[1], 
             label=label)
plt.legend()
plt.show()

# строим график апостериорных распределений для beta (alpha2, beta2) 
# априорных распределений
for i in [(0, 0), (n_1, y_1), (n_2, y_2),(n, y_total)]:
    label  = f"n = {i[0]}, y = {i[1]}"
    plt.plot(my_posterior(alpha2, beta2, i[0], i[1])[0],  
             my_posterior(alpha2, beta2, i[0], i[1])[1], 
             label=label)
plt.legend()
plt.show();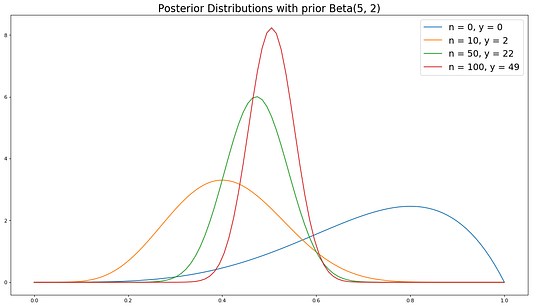
Апостериорное распределение имитированных бросков монеты со смещением для орла
Апостериорное распределение имитированных бросков монеты со смещением для решки

Как видите, при увеличении количества данных очень разные априорные распределения сходятся к одинаковому апостериорному распределению.

# строим график для обоих апостериорных распределений после 100
# бросков монеты
plt.plot(my_posterior(alpha1, beta1, n, y_total)[0],
         my_posterior(alpha1, beta1, n, y_total)[1])
plt.plot(my_posterior(alpha2, beta2, n, y_total)[0],
         my_posterior(alpha2, beta2, n, y_total)[1])
plt.show();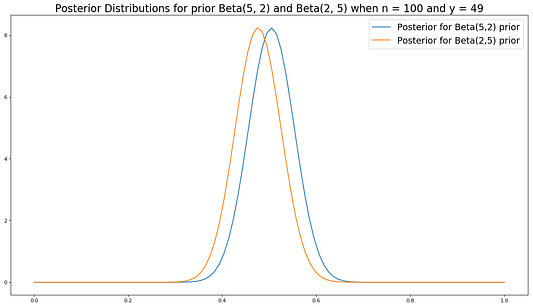

Как отмечалось выше, в байесовском подходе параметры случайны. Поэтому для вывода применяется другой язык. В частотном подходе есть «доверительные интервалы» — уверенность на X%, что истинный параметр находится в этом интервале. Это означает, что если взято бесконечное число выборок фиксированного размера, X% доверительных интервалов будут содержать истинный параметр. Это не означает, что существует X% вероятности того, что истинный параметр находится в доверительном интервале. Он либо входит, либо не входит в доверительный интервал. Мы просто не знаем.

В байесовском подходе есть «байесовские доверительные интервалы» —  существует вероятность X%, что параметр наблюдается в этом интервале. Это тонкое различие в языке с большими различиями в интерпретации. Статистики — это юристы математических дисциплин. 

Аналитически вывести апостериорное распределение не всегда бывает легко. Это одна из причин, почему частотный подход доминировал над байесовским в XX веке. С ростом вычислительных мощностей компьютеров практичнее стало использовать численные методы для генерации апостериорных распределений. Если вы зашли так далеко, у вас уже достаточно знаний для изучения этих алгоритмов.

Байесовские рассуждения как жизненная установка

Теперь, когда у вас есть базовые знания о байесовской точке зрения, я поясню, почему считаю байесовские рассуждения хорошей жизненной установкой. Это не самая новая перспектива, но большинство людей всё ещё не используют байесовский подход в реальности, поэтому стоит дать пояснение.

Любой согласится с тем, что 1×1=1, кроме разве что Теренса Ховарда. Нам не нужно вычислять степень уверенности в этом утверждении, потому что оно логически верно. Но множество других вещей требуют логических доказательств.

Давайте для примера возьмём вопрос об увеличении минимальной оплаты труда до $15,00 в час (горячая тема для дебатов в США). В то время как большинство дотошных людей считают, что размер увеличения минимальной заработной платы должен зависеть от прожиточного минимума в регионе (это априорное распределение), большинство популярных дискуссий принимает бинарную форму “нужно увеличивать до $15,00 в час, потому что это поможет большому числу людей” или “не нужно увеличивать минимальную заработную плату, потому что бизнес сократит занятость”, что предполагает эластичность спроса на рабочую силу для сегмента, содержащего должности с минимальной заработной платой.

К счастью, в некоторых штатах и муниципалитетах недавно увеличили минимальную заработную плату. В ближайшие месяцы и годы мы получим исследовательские работы, которые подтвердят или опровергнут наши ожидания, и мы сможем обновить их согласно байесовскому подходу. Люди, не придерживающиеся байесовского подхода, останутся при своём мнении вне зависимости от доказательств.

Я считаю, что этот подход стоит применять к большинству жизненных вопросов. У всех нас есть априорные убеждения, основанные на личных психических моделях того, как работает мир, но наши убеждения должны быть чувствительны к реальности. Когда доказательств убеждений недостаточно, не стоит слишком сильно держаться за них.

Закончу Правилом Кромвеля:

“Заклинаю вас всеми страстями христовыми — задумайтесь на минуту о том, что можете ошибаться.” — Оливер Кромвель

Читайте также:

Читайте нас в Telegram, VK и Яндекс.Дзен

Перевод статьи John Clements: Bayesian Stats 101 for Data Scientists

Предыдущая статьяСупергеройский макет: комбинируем CSS-сетки и CSS-фигуры
Следующая статьяЗнакомьтесь, компонент Navigation в Android!