8 базовых понятий статистики для науки о данных

Статистика — это разновидность математического анализа, использующая количественные модели и репрезентации для анализа экспериментальных или реальных данных. Главное преимущество статистики — простота представления информации. Недавно я пересматривала материалы по статистике и выделила 8 основных понятий, которые должен знать каждый специалист по обработке данных:

• дескриптивная аналитика;
• вероятность;
• среднее значение;
• изменчивость;
• взаимозависимость переменных;
• вероятностное распределение;
• проверка гипотезы и статистическая значимость;
• регрессия.

Дескриптивная аналитика

Дескриптивная аналитика описывает события в прошлом и помогает бизнесу оценить эффективность деятельности, предоставляя всем участникам процесса контекст, необходимый для интерпретации информации.

Вероятность

Вероятность — это мера возможности наступления события при случайном эксперименте.

Дополнение: P(A)+P(A’) =1

Пересечение: P(A∩B)=P(A)P(B)

Объединение: P(A∪B)=P(A)+P(B)−P(A∩B)

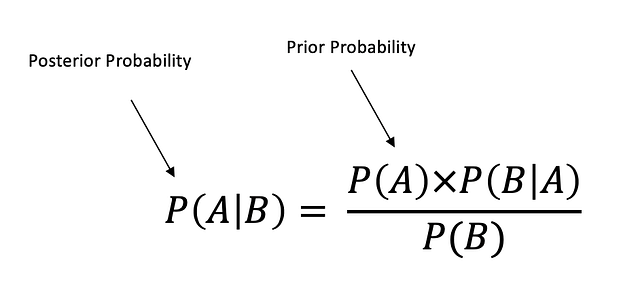
Условная вероятность: P(A|B) — это мера возможности наступления одного события по отношению к другому/-им событию/-ям. P(A|B)=P(A∩B)/P(B), когда P(B)>0.

Независимые события: два события считаются независимыми, если наступление одного из них не влияет на возможность наступления другого. P(A∩B)=P(A)P(B), где P(A) != 0 и P(B) != 0 , P(A|B)=P(A), P(B|A)=P(B).

Взаимоисключающие события: два события считаются взаимоисключающими, если оба они не могут произойти в одно и то же время. P(A∩B)=0 и P(A∪B)=P(A)+P(B).

Теорема Байеса описывает вероятность наступления события, исходя из ранее известной информации об условиях, которые могут иметь отношение к этому событию.

Среднее значение

Среднее арифметическое: среднее значение набора данных.

Медиана: срединное значение упорядоченного набора данных.

Мода: наиболее часто встречающееся значение в наборе данных. Если таких значений несколько, это называется мультимодальным распределением.

Асимметрия: мера симметричности.

Эксцесс: мера, показывающая медленное или быстрое убывание “хвоста” данных относительно нормального распределения.

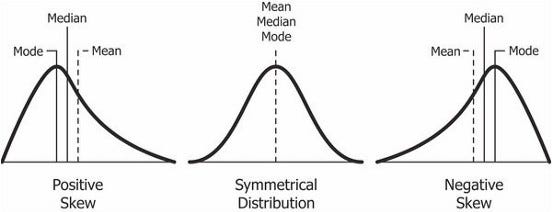
Positive Skew — Положительная асимметрия
Symmetrical Distribution — Симметричное распределение
Negative Skew — Отрицательная асимметрия
Mode — Мода
Median — Медиана
Mean — Среднее арифметическое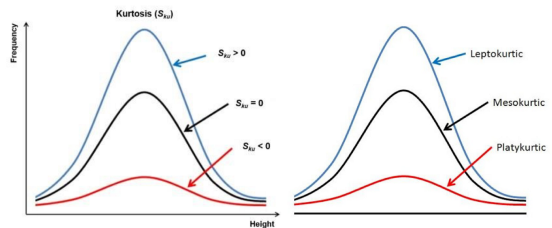

Kurtosis - Эксцесс
Frequency - Частота
Height - Высота
Leptokurtic - Положительный эксцесс
Mesokurtic - Нормальный эксцесс
Platykurtic - Отрицательный эксцесс

Изменчивость

Амплитуда: разница между минимальным и максимальным значениями в наборе данных.

Межквартильный размах (IQR): IQR = Q3−Q1

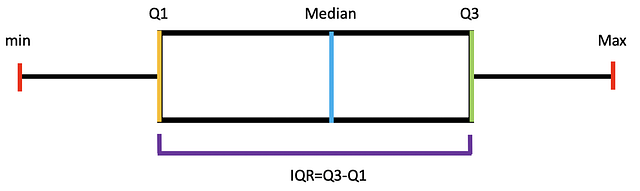
Min - Минимум
Max - Максимум
Median - Медиана

Дисперсия: среднеквадратичное отклонение значений от среднего арифметического, показывающее разброс данных относительно него.

Стандартное отклонение: стандартный разброс между каждым отдельным значением и средним арифметическим, квадратный корень из дисперсии.

Sample Variance - Выборочная дисперсия
Population Variance - Генеральная дисперсия
Sample Standard Deviation - Выборочное стандартное отклонение
Population Standard Deviation - Генеральное стандартное отклонение

Среднеквадратическая ошибка (SE): приблизительная величина стандартного отклонения выборочного распределения.

Взаимозависимость переменных

Причинность: такая зависимость между двумя событиями, когда одно из них влияет на другое.

Ковариантность: количественная мера совокупной изменчивости двух или более переменных.

Корреляция: мера взаимозависимости между двумя переменными с коэффициентом от -1 до 1, нормализованная версия ковариантности.

Positive Relationship - Прямая зависимость
Negative Relationship - Обратная зависимость
No Relationship - Отсутствие зависимости

Вероятностное распределение

Функции вероятностного распределения

Функция распределения масс (PMF): функция, которая указывает, что дискретная случайная переменная в точности равна какому-либо значению.

Функция плотности вероятности (PDF): функция для непрерывных данных, согласно которой значение в любой выборке может расцениваться как добавляющее относительной вероятности тому, что значение случайной переменной равно значению этой выборки.

Функция кумулятивной плотности (CDF): функция, которая указывает, что случайная переменная меньше определённого значения или равна ему.

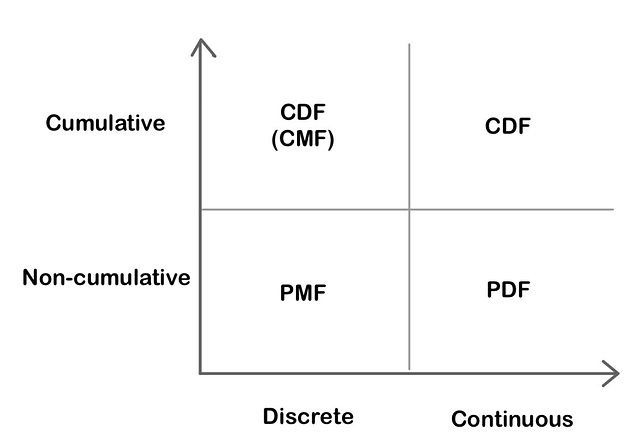
Cumulative - Кумулятивный
Non-cumulative - Некумулятивный
Discrete - Дискретный
Continuous - Непрерывный

Непрерывное распределение вероятностей

Равномерное распределение: распределение, при котором все исходы имеют одинаковую вероятность (также известно как прямоугольное распределение).

Нормальное/гауссово распределение: кривая распределения имеет форму колокола и симметрична. Согласно центральной предельной теореме, выборочное распределение средних арифметических приближается к нормальному при увеличении объёма выборки.

Uniform Distribution - Равномерное распределение
Normal Distribution - Нормальное распределение

Экспоненциальное распределение: вероятностное распределение времени между событиями в пуассоновском точечном процессе.

Распределение хи-квадрат: распределение суммы квадратов стандартных нормальных отклонений.

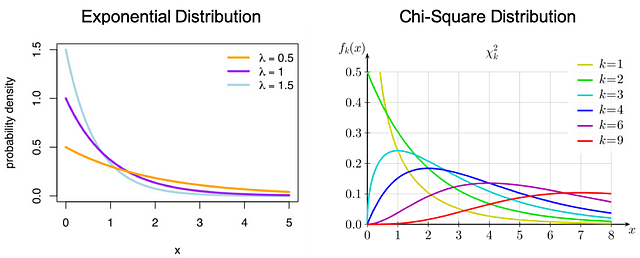
Exponential Distribution - Экспоненциальное распределение
Chi-Square Distribution - Распределение хи-квадрат
Probability Density - Плотность вероятностей

Дискретное распределение вероятностей

Распределение Бернулли: распределение случайной переменной, при котором для наступления события есть одна попытка и 2 возможных исхода: 1 — успех с вероятностью p и 0 — неудача с вероятностью 1-p.

Биномиальное распределение: распределение некоторого количества успешных исходов события в количестве n независимых экспериментов. У каждого события есть только 2 возможных исхода: 1 — успех с вероятностью p и 0 — неудача с вероятностью 1-p.

Распределение Пуассона: распределение, которое отражает вероятность заданного числа событий k, происходящих в течение фиксированного промежутка времени, если эти события наступают с известной постоянной усреднённой вероятностью λ и независимо от времени.

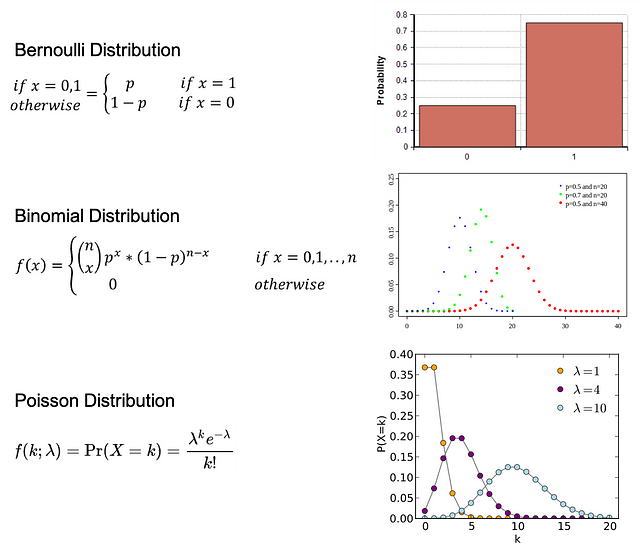
Bernoulli Distribution - Распределение Бернулли
Binomial Distribution - Биномиальное распределение
Poisson Distribution - Распределение Пуассона
Probability - Вероятность
If - Если
Otherwise - Иначе

Проверка гипотезы и статистическая значимость

Нулевая и альтернативная гипотезы

Нулевая гипотеза: общее утверждение, согласно которому между измеряемыми явлениями или их группами нет взаимозависимости.

Альтернативная гипотеза: гипотеза, обратная нулевой.

При проверке статистической гипотезы ошибка типа I — это непринятие истинной нулевой гипотезы, а ошибка типа II — принятие ложной нулевой гипотезы.

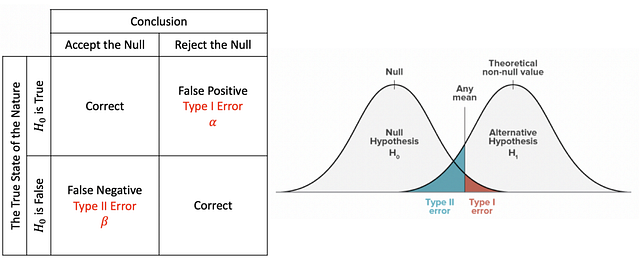
The True State of the Nature - Истинное положение вещей
False - Ложь
True - Истина
Conclusion - Вывод
Accept the Null - Принятие нуля
Reject the Null - Непринятие нуля
Correct - Верно
False Negative - Ложный отрицательный
False Positive - Ложный положительный
Type I Error - Ошибка типа I
Type II Error - Ошибка типа II
Any mean - Любое среднее арифметическое
Theoretical non-null value - Теоретическое ненулевое значение
Null Hypothesis - Нулевая гипотеза
Alternative Hypothesis - Альтернативная гипотеза

Интерпретация

P-значение: вероятность того, что данная статистика будет иметь как минимум такие же экстремальные значения, как и ранее наблюдаемая, при условии, что нулевая гипотеза верна. Когда p-значение > α, нулевую гипотезу невозможно не принять, в том время как если p-значение ≤ α, нулевая гипотеза не принимается, следовательно, мы имеем статистически значимый результат.

Критическое значение: точка на шкале статистики, выше которой нулевая гипотеза не принимается (зависит от уровня значимости проверки, α). Значение зависит от статистики (отдельная для каждого типа проверки) и уровня значимости проверки α (определяет точность проверки).

Уровень значимости и область непринятия: область непринятия зависит от уровня значимости. Уровень значимости (α) — это вероятность непринятия нулевой гипотезы при условии, что она верна.

Z-тест

Z-тест — это статистическая проверка, при которой распределение статистики при нулевой гипотезе может приближаться к нормальному, а также проверяет среднее арифметическое распределения при известной генеральной дисперсии. Следовательно, при больших объёмах выборки или известной генеральной дисперсии многие статистические проверки удобно проводить в форме Z-тестов.

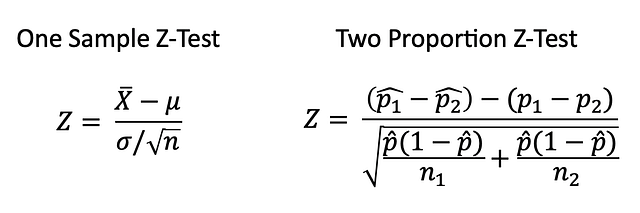
One Sample Z-Test - Z-тест одной выборки
Two Proportion Z-Test - Z-тест двух долей

T-тест

T-тест — это статистическая проверка, используемая, когда генеральная дисперсия неизвестна, а объём выборки небольшой (n < 30).

Парная выборка означает, что сбор данных производится дважды с одной и той же группы, человека, образца, предмета. Независимая выборка подразумевает, что две выборки должны быть получены с двух абсолютно разных совокупностей.

One Sample T-Test - T-тест одной выборки
Two Sample T-Test - T-тест двух выборок
Paired Sample - Парная выборка
Independent Sample - Независимая выборка
Equal/Unequal Sample Size - Одинаковый/неодинаковый объём выборки
Not Variance - Без дисперсии
Similar Variance - Одинаковая дисперсия
Unequal Variance - Неодинаковая дисперсия
Where - Где

ANOVA(дисперсионный анализ)

Аназиз ANOVA позволяет выяснить, являются ли результаты эксперимента статистически значимыми. При однофакторном дисперсионном анализе сравниваются два средних арифметических двух независимых групп с помощью одной независимой переменной. Двухфакторный дисперсионный анализ — продолжение однофакторного, здесь для вычисления главного эффекта и эффекта взаимодействия используются две независимые переменные.

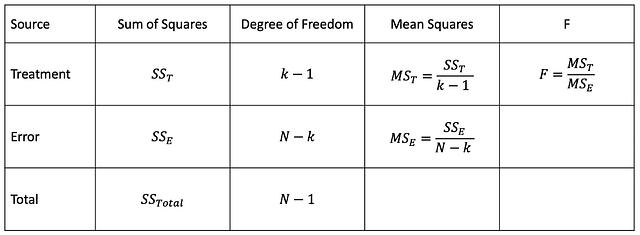
Source - Источник
Sum of Squares - Сумма квадратов
Degree of Freedom - Степень свободы
Mean Squares - Квадраты средних арифметических
Treatment - Комбинация условий
Error - Ошибка
Total - Итог

Тест хи-квадрат

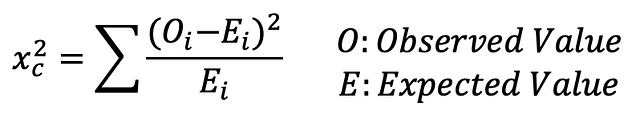
Observed Value - Наблюдаемая величина
Expected Value - Ожидаемая величина

Тест хи-квадрат определяет, соответствует ли модель нормальному распределению при введении набора дискретных данных. Критерий согласия определяет, соответствует ли распределению выборка совокупности одной категориальной переменной. Критерий независимости хи-квадрат позволяет проверить два набора данных на предмет наличия взаимосвязи.

Регрессия

Линейная регрессия

Постулаты линейной регрессии:

• линейная зависимость;
• многомерная нормальность;
• небольшая мультиколлинеарность или её отсутствие;
• небольшая автокорреляция или её отсутствие;
• гомоскедастичность.

Линейная регрессия — это линейный подход к моделированию взаимозависимости между зависимой и независимой переменными. Независимая переменная — это контролируемая в ходе научного эксперимента переменная, используемая для измерения влияния на зависимую переменную. Зависимая переменная — это переменная, измеряемая в ходе научного эксперимента.

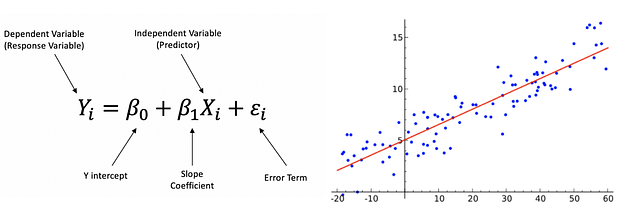
Dependent (Response) Variable - Зависимая переменная
Predictor - Регрессор
Y Intercept - Отрезок по оси Y
Slope Coefficient - Коэффициент наклона
Error Term - Величина погрешности

Множественная линейная регрессия — это линейный подход к моделированию взаимозависимости между одной зависимой и двумя или более независимыми переменными.

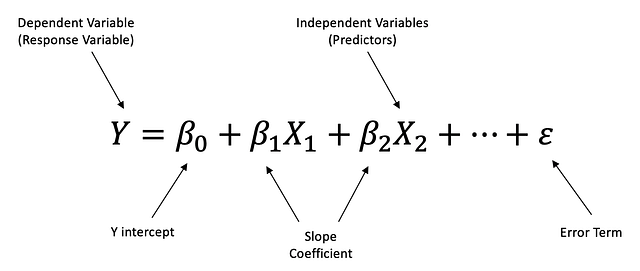
Этапы построения линейной регрессии

Этап 1: Проанализируйте описание модели, причинные зависимости и направленность.

Этап 2: Проверьте данные, в том числе категориальные, недостающие и выбросы.

• Выброс — это образец данных, значительно отличающийся от других наблюдений. Можно использовать метод стандартного отклонения и межквартильного размаха (IQR).
• Вспомогательная переменная принимает только 0 и 1 в качестве значения и отражает влияние на категориальные переменные.

Этап 3: Простой анализ — проверьте результат сравнения независимой и зависимой переменных, а также двух независимых переменных.

• Используйте диаграмму рассеивания для проверки взаимозависимости.
• Когда более двух независимых переменных имеют сильную взаимосвязь, это называется мультиколлинеарностью. Для количественной оценки можно использовать фактор, увеличивающий дисперсию (VIF): если VIF > 5, между переменными существует сильная взаимосвязь, если VIF > 10, между переменными возникает мультиколлинеарность.
• Величина взаимодействия отражает изменения в наклоне кривой между значениями.

Этап 4: Множественная линейная регрессия — проверьте модель и истинные переменные.

Этап 5: Остаточный анализ.

• Проверьте нормальное распределение, а также соответствуют ли ему остатки.
• Гомоскедастичность описывает ситуацию, когда величина погрешности одинакова для всех значений независимых переменных, следовательно, значения остатков также одинаковы на протяжении всей кривой регрессии.

Этап 6: Интерпретация результатов регрессии.

• R-квадрат — это статистический показатель точности подбора, который указывает, насколько отклонение зависимой переменной было отражено независимыми переменными. Более высокие значения R-квадрата указывают, что разница между данными наблюдений и подобранными значениями небольшая.
• P-значение.
• Уравнение регрессии.

Читайте также:

• Как искусственный интеллект меняет финансовый сектор?
• 14 проектов по науке о данных для вашего 14-дневного карантина
• Моделирование экспоненциального роста

---

Перевод статьи Shirley Chen: The 8 Basic Statistics Concepts for Data Science