Линейная регрессия — реализация на Python

Примечание: Для упрощения в этой статье зависимые переменные называются откликами, независимые — признаками. Чтобы обеспечить базовое понимание линейной регрессии, мы начнем с самой базовой версии линейной регрессии, то есть простой линейной регрессии.

Что такое линейная регрессия?

Линейная регрессия — это метод из статистики. Он используется для прогнозирования непрерывной зависимой переменной (целевой переменной) по одной или нескольким независимым переменным (для прогноза). Этот метод предполагает линейную связь между зависимыми и независимыми переменными. Это означает, что зависимая переменная изменяется пропорционально изменениям независимых переменных. Другими словами, линейная регрессия используется для определения степени, в которой одна или несколько переменных могут спрогнозировать значение зависимой переменной.

Допущения, которые делаются в модели линейной регрессии:

Ниже приведены основные допущения, которые делает модель линейной регрессии в отношении набора данных, где применяется:  

• Линейная связь. Взаимосвязь между переменными отклика и функции должна быть линейной. Предположение о линейности можно проверить с помощью диаграмм рассеяния. Как показано ниже, 1-й рисунок представляет линейно связанные переменные, тогда как переменные на 2-м и 3-м рисунках, скорее всего, являются нелинейными. Итак, первый рисунок даст лучшие прогнозы с использованием линейной регрессии. 

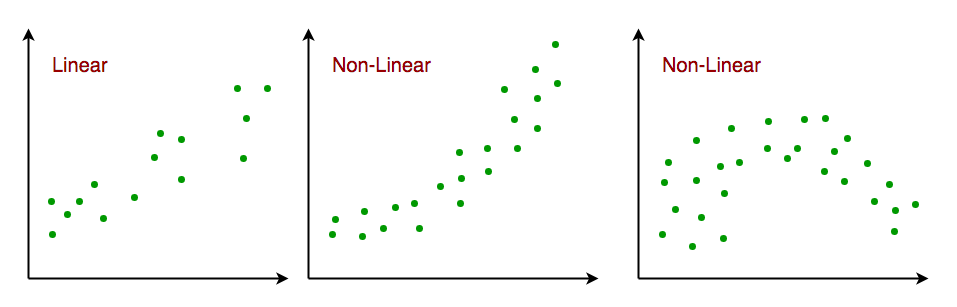
• Мультиколлинеарность незначительная или отсутствует. Предполагается, что мультиколлинеарность в данных небольшая или отсутствует. Мультиколлинеарность возникает, когда признаки (или независимые переменные) не являются независимыми друг от друга.
• Автокорреляция незначительна или отсутствует. Другое предположение состоит в том, что автокорреляция в данных небольшая или вообще отсутствует. Автокорреляция возникает, когда остаточные ошибки не являются независимыми друг от друга.
• Нет выбросов. Предполагается, что в данных нет выбросов. Выбросы — это точки данных, которые находятся далеко от остальных данных. Выбросы могут повлиять на результаты анализа.
• Гомоскедастичность. Гомоскедастичность описывает ситуацию, когда член ошибки (то есть «шум» или случайное нарушение во взаимоотношениях между независимыми переменными и зависимой переменной) является одинаковым для всех значений независимых переменных. Как показано ниже, диаграмма на рисунке 1 обладает гомоскедастичностью, а рисунок 2 — гетероскедастичностью. 

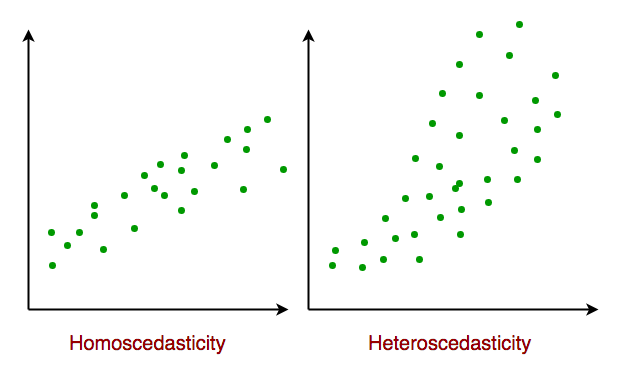
В конце статьи рассмотрим некоторые приложения линейной регрессии. 

Виды линейной регрессии

Существует два основных типа линейной регрессии:

• Простая линейная регрессия. Это прогнозирование зависимой переменной на основе одной независимой переменной.
• Множественная линейная регрессия. Она предполагает прогнозирование зависимой переменной на основе нескольких независимых переменных.

Простая линейная регрессия

Простая линейная регрессия – это подход к прогнозированию ответа с помощью одного признака. Это одна из самых базовых моделей машинного обучения, о которых должен знать энтузиаст в области ML. В линейной регрессии предполагается, что две переменные, то есть зависимая и независимые переменные связаны линейно. Следовательно, мы пытаемся найти линейную функцию, которая предельно точно агонизирует значение отклика (y) как функцию признака или независимой переменной (x). Давайте рассмотрим набор данных, где есть значение ответа y для каждого признака x: 

Для общности определим:

x как вектор признаков, т.е. x = [x_1, x_2, …., x_n],

y как вектор откликов, т.е. y = [y_1, y_2, …., y_n].

для n наблюдений (в приведенном примере n=10). Диаграмма рассеяния вышеуказанного набора данных выглядит следующим образом:

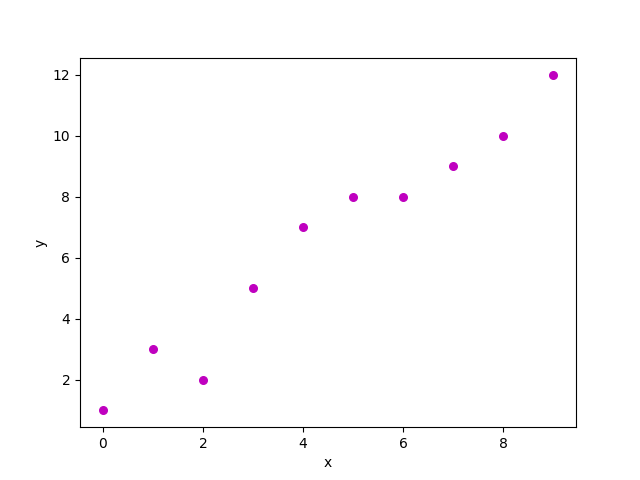
Теперь задача состоит в том, чтобы найти линию, которая наилучшим образом соответствует приведенной выше диаграмме рассеяния, такую, что она прогнозирует отклик для любых новых значений признаков (т. е. значение x, отсутствующее в наборе данных). Эта линия называется линией регрессии. Уравнение линии регрессии представлено в виде:

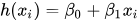
Здесь:

• h(x_i) представляет собой прогнозируемое значение отклика для i-^го наблюдения.
• b_0 и b_1 являются коэффициентами регрессии и представляют собой пересечение оси y и наклон линии регрессии соответственно.

Чтобы создать нашу модель, мы должны «узнать» или оценить значения коэффициентов регрессии b_0 и b_1. Оценив эти коэффициенты, мы можем использовать модель для прогнозирования ответов!
В этой статье мы будем использовать метод наименьших квадратов.

Посмотрите на формулу:

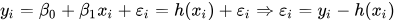
Здесь e_i — это остаточная ошибка в i-м наблюдении. Итак, наша цель — минимизировать общую остаточную ошибку. Квадрат ошибки или функция стоимости J определяется как:

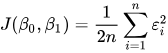
И наша задача — найти значение b₀ и b₁, для которого J(b₀, b₁) наименьшее! Не вдаваясь в математические подробности, приведем результат:

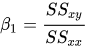
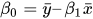
Где SS_xy — сумма перекрестных отклонений y и x:

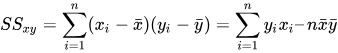
А SS_xx — сумма квадратов отклонений от x:

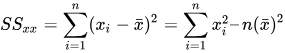
Реализация простой линейной регрессии на Python 

Мы можем использовать язык Python для изучения коэффициентов моделей линейной регрессии. Для построения графика исходных данных и наилучшей линии задействуем библиотеку matplotlib. Это одна из самых используемых библиотек Python для построения графиков. Вот пример простой линейной регрессии с помощью Python.

Импорт библиотек

import numpy as np
import matplotlib.pyplot as plt

Функция оценки коэффициентов

Эта функция, estimate_coef(), принимает входные данные x (независимая переменная) и y (зависимая переменная) и оценивает коэффициенты прямой линейной регрессии методом наименьших квадратов.

• Вычисление количества наблюдений: n = np.size(x) определяет количество точек данных.
• Вычисление средних значений: m_x = np.mean(x) и m_y = np.mean(y) вычисляют средние значения x и y соответственно.
• Вычисление поперечного отклонения и отклонения относительно x: SS_xy = np.sum(y*x) - n*m_y*m_x и SS_xx = np.sum(x*x) - n*m_x*m_x вычисляют сумму квадратов отклонений между x и y и сумму квадратов отклонений x относительно своего среднего соответственно.
• Вычисление коэффициентов регрессии: b_1 = SS_xy / SS_xx и b_0 = m_y - b_1*m_x определяет наклон (b_1) и наклон (b_0) линии регрессии, используя метод наименьших квадратов.
• Возврат коэффициентов: Функция возвращает оцененные коэффициенты в виде кортежа (b_0, b_1).

def estimate_coef(x, y):
  # количество наблюдений/точек
  n = np.size(x)

  # среднее значение вектора x и y
  m_x = np.mean(x)
  m_y = np.mean(y)

  # вычисление поперечного отклонения и отклонения относительно x
  SS_xy = np.sum(y*x) - n*m_y*m_x
  SS_xx = np.sum(x*x) - n*m_x*m_x

  # вычисление коэффициентов регрессии
  b_1 = SS_xy / SS_xx
  b_0 = m_y - b_1*m_x

  return (b_0, b_1)

Построение функции линейной регрессии

Функция plot_regression_line() принимает входные данные x (независимая переменная), y (зависимая переменная) и расчетные коэффициенты b, чтобы построить точки данных и прямую регрессии.

1. Построение диаграммы рассеяния: plt.scatter(x, y, color = "m", marker = "o", s = 30) строит исходные точки данных в виде диаграммы рассеяния красными точками ???.
2. Вычисление прогнозируемого вектора отклика: y_pred = b[0] + b[1]*x вычисляет прогнозируемые значения y по оценке коэффициентов b.
3. Построение прямой регрессии: plt.plot(x, y_pred, color = "g") строит линию регрессии, используя срогнозированные значения и независимые переменная x.
4. Добавление меток: plt.xlabel('x') и plt.ylabel('y') обозначают ось x как 'x' и ось y как 'y' соответственно.

def plot_regression_line(x, y, b):
  # построение диаграммы рассеяния фактических точек
  plt.scatter(x, y, color = "m",
        marker = "o", s = 30)

  # вектор прогнозируемого отклика
  y_pred = b[0] + b[1]*x

  # построение линии регрессии
  plt.plot(x, y_pred, color = "g")

  # нанесение меток
  plt.xlabel('x')
  plt.ylabel('y')

Вывод: 

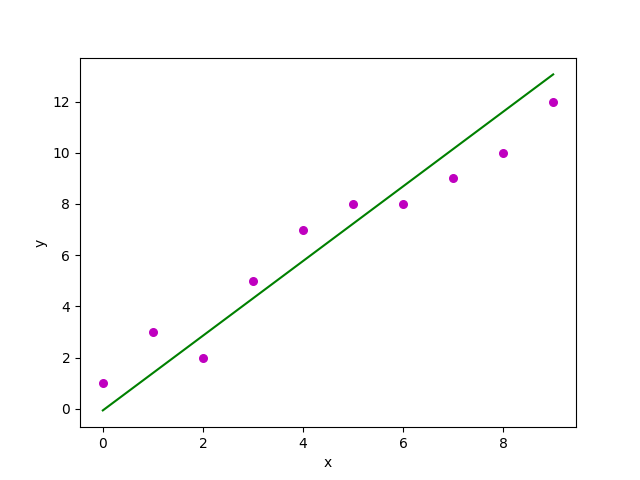
Основная функция

Предоставленный код реализует простой линейный регрессионный анализ путем определения функции main(), которая выполняет следующие шаги:

1. Определение данных: Определяет независимую переменную (x) и зависимую переменную (y) как массивы NumPy.
2. Оценка коэффициента: Вызывает функцию estimate_coef() для определения коэффициентов линии линейной регрессии с использованием предоставленных данных.
3. Печать коэффициентов. Печатает расчетную точку пересечения (b_0) и наклон линии регрессии (b_1).

def main():
  # наблюдения / данные
  x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
  y = np.array([1, 3, 2, 5, 7, 8, 8, 9, 10, 12])

  # оценка коэффициентов
  b = estimate_coef(x, y)
  print("Estimated coefficients:\nb_0 = {} \
     \nb_1 = {}".format(b)

Вывод: 

Estimated coefficients:
b_0 = 1.2363636363636363
b_1 =  1.1696969696969697

Множественная линейная регрессия

Множественная линейная регрессия пытается смоделировать взаимосвязь между двумя или более признаками и откликом путем подгонки линейного уравнения к наблюдаемым данным. Очевидно, что это не что иное, как расширение простой линейной регрессии. Рассмотрим набор данных с функциями p (или независимыми переменными) и одним ответом (или зависимой переменной). Кроме того, набор данных содержит n строк/наблюдений. 

Определим следующее:

X (матрица признаков) = матрица размера n X p, где x_ij обозначает значения j^-го признака для i-го наблюдения.

 Так,

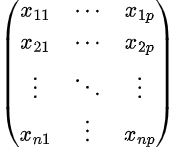
и y (вектор откликов) = вектор размера n, где y_{i} обозначает значение отклика для i-го наблюдения:

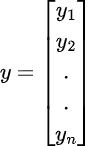
Линия регрессии для объектов p представлена ​​как: 

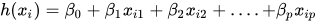
где h(x_i) — прогнозируемое значение ответа для i-го наблюдения, а b_0, b_1, …, b_p — коэффициенты регрессии. Также можно написать: 

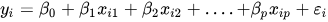
или

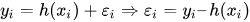
где e_i представляет остаточную ошибку в i-м наблюдении. Можно еще немного обобщить нашу линейную модель, представив матрицу признаков X как:

Итак, теперь линейную модель можно выразить через матрицы следующим образом: 

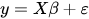
где 

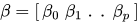
и

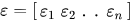
Определим оценку b, т. е. b’, используя метод наименьших квадратов. Как уже объяснялось, метод наименьших квадратов имеет тенденцию определять b’, для которого общая остаточная ошибка минимальна. Представим результат прямо здесь: 

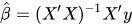
где ‘ представляет транспонирование матрицы, а -1 — обратную матрицу. Зная оценки наименьших квадратов, b’, модель множественной линейной регрессии теперь можно оценить как:

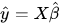
где y’ — это предполагаемый вектор отклика.

Реализация множественной линейной регрессии на языке Python

Для множественной линейной регрессии с помощью Python мы будем использовать набор данных о ценах на дома в Бостоне. 

Импорт библиотек

from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metrics
import pandas as pd

Загрузка базы данных о жилье Бостона

Код загружает набор данных Boston Housing с предоставленного URL-адреса и считывает его в DataFrame Pandas (raw_df).

data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+",
           skiprows=22, header=None)

Предварительная обработка данных

При этом из фрейма DataFrame извлекаются входные переменные (X) и целевая переменная (y). Входные переменные выбираются из каждого второго ряда, чтобы соответствовать целевой переменной, которая имеется в каждом втором ряду.

X = np.hstack([raw_df.values[::2, :],
        raw_df.values[1::2, :2]])
y = raw_df.values[1::2, 2]

Разделение данных на обучающие и тестовые наборы

Здесь данные разделяются на наборы для обучения и тестирования с помощью функции train_test_split() из scikit-learn. Параметр test_size указывает, что для тестирования должно использоваться 40% данных.

X_train, X_test,\
  y_train, y_test = train_test_split(X, y,
                    test_size=0.4,
                    random_state=1)

Создание и обучение модели линейной регрессии

При этом инициализируется объект LinearReгрессия (reg) и модель обучается с использованием обучающих данных (X_train, y_train)

reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)

Вычисление эффективности модели

Производительность модели оценивается путем [\вычисления и] печати коэффициентов регрессии и расчета показателя дисперсии, который измеряет долю объясненной дисперсии. Оценка 1 означает идеальный прогноз.

# коэффициенты регрессии
print('Coefficients: ', reg.coef_)

# оценка дисперсии: 1 означает идеальный прогноз
print('Variance score: {}'.format(reg.score(X_test, y_test)))

Вывод: 

Coefficients:
[ -8.80740828e-02   6.72507352e-02   5.10280463e-02   2.18879172e+00
-1.72283734e+01   3.62985243e+00   2.13933641e-03  -1.36531300e+00
2.88788067e-01  -1.22618657e-02  -8.36014969e-01   9.53058061e-03
-5.05036163e-01]
Variance score: 0.720898784611

Отображение остаточных ошибок в виде графика

Построение графика и анализ остаточных ошибок, которые представляют собой разницу между прогнозируемыми и фактическими значениями.

# график остаточной ошибки

# стиль графика
plt.style.use('fivethirtyeight')

# построение графика остаточных ошибок в тренировочных данных
plt.scatter(reg.predict(X_train),
            reg.predict(X_train) - y_train,
            color="green", s=10,
            label='Train data')

# построение графика остаточных ошибок в тестовых данных
plt.scatter(reg.predict(X_test),
            reg.predict(X_test) - y_test,
            color="blue", s=10,
            label='Test data')

# построение линии для нулевой остаточной ошибки
plt.hlines(y=0, xmin=0, xmax=50, linewidth=2)

# построение легенды
plt.legend(loc='upper right')

# название графика
plt.title("Residual errors")

# вызов метода для отображения графика
plt.show()

Вывод: 

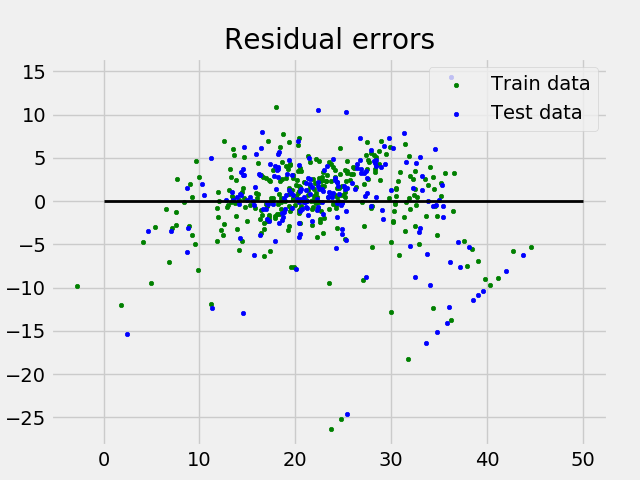
График остаточных ошибок множественной линейной регрессии

В приведенном выше примере точность определяется при помощи показателя объясненной дисперсии. Пусть:

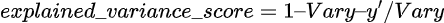
где y’ — предполагаемый целевой результат, y — соответствующий (корректный) целевой результат, а Var — дисперсия, квадрат стандартного отклонения. Наилучшая возможная оценка — 1,0, значения ниже — оценка хуже.

Полиномиальная линейная регрессия

Полиномиальная регрессия – это форма линейной регрессии, в которой взаимосвязь между независимой переменной x и зависимой переменной y моделируется полиномом n-й степени. Полиномиальная регрессия соответствует нелинейной зависимости между значением x и соответствующим условным средним значением y, обозначаемым E (y | x).

Подбор степени полиномиальной регрессии

Подбор степени полиномиальной регрессии — это компромисс между предвзятостью и дисперсией. Смещение — это тенденция модели последовательно прогнозировать одно и то же значение, независимо от истинного значения зависимой переменной. Дисперсия — это тенденция модели делать разные прогнозы для одной и той же точки данных в зависимости от конкретных обучающих данных.

Полином более высокой степени может сократить смещение, но может увеличить дисперсию, что приведет к переобучению. И наоборот, полином более низкой степени может уменьшить дисперсию, но может и увеличить смещение.

Существует ряд методов выбора степени полиномиальной регрессии, например перекрестная проверка и использование информационных критериев, таких как информационный критерий Акаике (AIC) или байесовский информационный критерий (BIC).

Реализация полиномиальной регрессии на Python

Реализация полиномиальной регрессии на Python:

Здесь мы импортируем все необходимые библиотеки для анализа данных и задач машинного обучения, а затем загрузим набор данных Position_Salaries.csv с помощью Pandas. Затем Pandas подготавливает данные для моделирования, обрабатывая пропущенные значения и кодируя категориальные данные. Наконец, она разбивает данные на наборы для обучения и тестирования, а таже стандартизирует числовые признаки с помощью StandardScaler.

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn
import warnings

from sklearn.preprocessing import LabelEncoder
from sklearn.impute import KNNImputer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import f1_score
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import cross_val_score

warnings.filterwarnings('ignore')

df = pd.read_csv('Position_Salaries.csv')

X = df.iloc[:,1:2].values
y = df.iloc[:,2].values

Вывод:

array([[      1,   45000,       0],
       [      2,   50000,       4],
       [      3,   60000,       8],
       [      4,   80000,       5],
       [      5,  110000,       3],
       [      6,  150000,       7],
       [      7,  200000,       6],
       [      8,  300000,       9],
       [      9,  500000,       1],
       [     10, 1000000,       2]], dtype=int64)

Код создает модель линейной регрессии и обучает её на предоставленных данных, устанавливая линейную связь между зависимыми и независимыми переменными.

from sklearn.linear_model import LinearRegression
lin_reg=LinearRegression()
lin_reg.fit(X,y)

Код выполняет квадратичную и кубичную регрессию, генерируя полиномиальные функции из исходных данных и подгоняя модели линейной регрессии к этим функциям. Это позволяет моделировать нелинейные связи между независимыми и зависимыми переменными.

from sklearn.preprocessing import PolynomialFeatures
poly_reg2=PolynomialFeatures(degree=2)
X_poly=poly_reg2.fit_transform(X)
lin_reg_2=LinearRegression()
lin_reg_2.fit(X_poly,y)

poly_reg3=PolynomialFeatures(degree=3)
X_poly3=poly_reg3.fit_transform(X)
lin_reg_3=LinearRegression()
lin_reg_3.fit(X_poly3,y)

Код создает диаграмму рассеяния точки данных. Он эффективно визуализирует линейную зависимость между уровнем должности и зарплатой.

plt.scatter(X,y,color='red')
plt.plot(X,lin_reg.predict(X),color='green')
plt.title('Simple Linear Regression')
plt.xlabel('Position Level')
plt.ylabel('Salary')
plt.show()

Вывод:

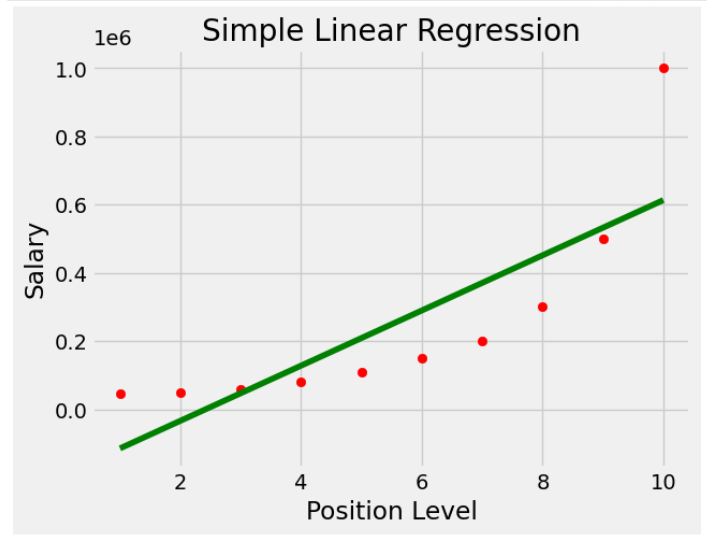
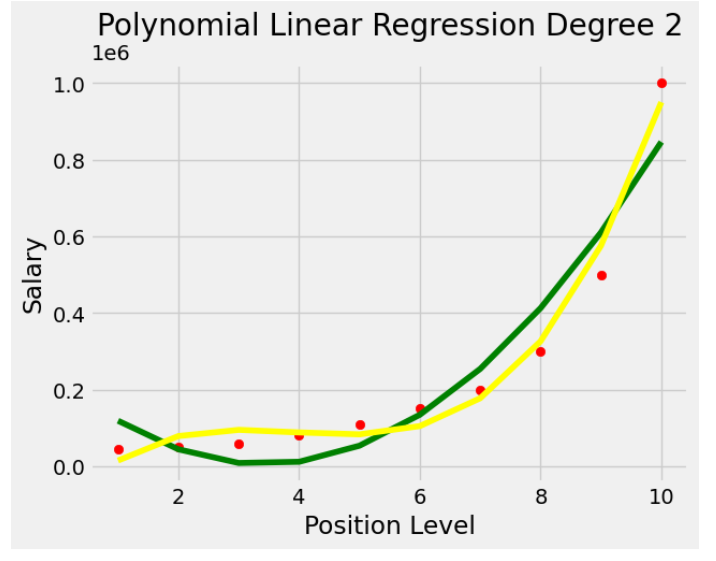
Код создает диаграмму рассеяния точек данных, накладывая прогнозируемые линии квадратичной и кубической регрессии. Он эффективно визуализирует нелинейную связь между уровнем должности и зарплатой и сравнивает соответствие моделей квадратичной и кубической регрессии.

plt.style.use('fivethirtyeight')
plt.scatter(X,y,color='red')
plt.plot(X,lin_reg_2.predict(poly_reg2.fit_transform(X)),color='green')
plt.plot(X,lin_reg_3.predict(poly_reg3.fit_transform(X)),color='yellow')
plt.title('Polynomial Linear Regression Degree 2')
plt.xlabel('Position Level')
plt.ylabel('Salary')
plt.show()

Вывод:

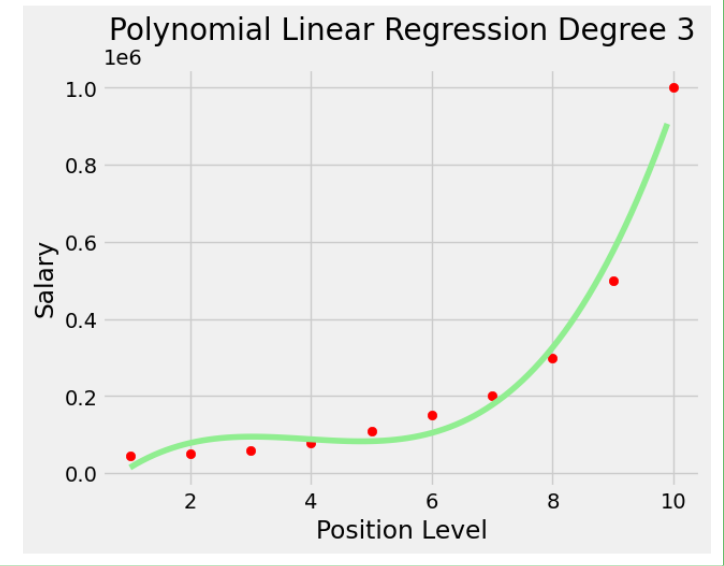
Код эффективно визуализирует взаимосвязь между уровнем должности и зарплатой с помощью кубической регрессии и генерирует непрерывную линию прогнозирования для более широкого диапазона уровней должностей.

plt.style.use('fivethirtyeight')
X_grid=np.arange(min(X),max(X),0.1) # Даст нам вектор. Мы должны преобразовать его в матрицу 
X_grid=X_grid.reshape((len(X_grid),1))
plt.scatter(X,y,color='red')
plt.plot(X_grid,lin_reg_3.predict(poly_reg3.fit_transform(X_grid)),color='lightgreen')

#plt.plot(X,lin_reg_3.predict(poly_reg3.fit_transform(X)),color='green')
plt.title('Polynomial Linear Regression Degree 3')
plt.xlabel('Position Level')
plt.ylabel('Salary')
plt.show()

Вывод:

Приложения линейной регрессии

• Линии тренда. Линия тренда представляет собой изменение количественных данных с течением времени (например, ВВП, цены на нефть и т. д.). Эти тенденции обычно подчиняются линейной зависимости. Следовательно, линейная регрессия может применяться для прогнозирования будущих значений. Однако этот метод страдает отсутствием научного обоснования в случаях, когда на данные могут повлиять другие потенциальные изменения.
• Экономика. Линейная регрессия — преобладающий эмпирический инструмент в экономике. Например, регрессия используется для прогнозирования потребительских расходов, инвестиций в основной капитал, инвестиций в товары, закупок экспортной продукции страны, расходов на импорт, спроса на владение ликвидными активами, спроса на рабочую силу и ее предложения.
• Финансы. Модель активов капитала использует линейную регрессию для анализа и количественной оценки систематических рисков инвестиций.
• Биология. Линейная регрессия используется для моделирования причинно-следственных связей параметров в биологических системах.

Преимущества линейной регрессии

• Легко интерпретировать. Коэффициенты модели линейной регрессии представляют собой изменение зависимой переменной при изменении независимой переменной на одну единицу, что упрощает понимание взаимосвязи переменных.
• Устойчива к выбросам. Линейная регрессия относительно устойчива к выбросам. Это означает, что по сравнению с другими статистическими методами экстремальные значения независимой переменной влияют на нее меньше.
• Может обрабатывать как линейные, так и нелинейные связи. Линейная регрессия может использоваться для моделирования как линейных, так и нелинейных связей переменных. Это связано с тем, что до использования в модели независимую перменную можно преобразовать [в зависимую].
• Нет необходимости масштабирования или преобразования признаков. В отличие от некоторых алгоритмов машинного обучения, линейная регрессия не требует масштабирования или преобразования признаков. Это может быть значительным преимуществом, особенно при работе с большими наборами данных.

Недостатки линейной регрессии

• Предполагает линейность. Линейная регрессия предполагает, что связь между независимой переменной и зависимой переменной является линейной. Это предположение может быть справедливым не для всех наборов данных. В случаях, когда зависимость нелинейная, лучшим выбором может оказаться линейная регрессия.
• Чувствительна к мультиколлинеарности. Линейная регрессия чувствительна к мультиколлинеарности. Это происходит, когда независимые прееменные обладают высокой корреляцией. Мультиколлинеарность может затруднить интерпретацию коэффициентов модели и привести к переобучению.
• Может не подходить для очень сложных отношений. Линейная регрессия может не подходить для моделирования очень сложных отношений между переменными. Например, она может быть не в состоянии моделировать отношения, содержащие взаимодействие между независимыми переменными.
• Не подходит для задач классификации. Линейная регрессия — это алгоритм регрессии, который не подходит для задач классификации, включающих прогнозирование категориальной переменной, а не непрерывной переменной.

Часто задаваемые вопросы (FAQ)

1. Как использовать линейную регрессию для прогнозирования?

После обучения модели линейной регрессии ее можно использовать для прогнозирования новых точек данных. Класс LinearReprofit в scikit-learn предоставляет метод Predict(), который можно использовать для прогнозирования.

2. Что такое линейная регрессия?

Линейная регрессия — это алгоритм машинного обучения с учителем (управляемый). Он используется для прогнозирования непрерывного численного результата. Предполагается, что связь между независимыми переменными (признаками) и зависимой переменной (целью) линейна, а это означает, что прогнозируемое значение цели можно рассчитать как линейную комбинацию признаков.

3. Как выполнить линейную регрессию в Python?

В Python есть несколько библиотек, которые можно использовать для выполнения линейной регрессии, включая scikit-learn, statsmodels и NumPy. Библиотека scikit-learn — самый популярный выбор для задач машинного обучения, она предоставляет простую и эффективную реализацию линейной регрессии.

4. Какие есть еще примеры линейной регрессии?

Линейная регрессия — это универсальный алгоритм, который можно использовать для самых разных приложений, включая финансы, здравоохранение и маркетинг. Некоторые конкретные примеры включают:

• Прогнозирование цен на жилье.
• Прогнозирование цен на акции.
• Диагностику заболеваний.
• Прогнозирование оттока клиентов.

5. Как линейная регрессия реализована в sklearn?

Линейная регрессия реализована в scikit-learn в классе LinearReprofit. Этот класс предоставляет методы для обучения модели линейной регрессии к набору обучающих данных и прогнозирования целевого значения для новых точек данных.

Читайте также:

• 6 шагов для старта в машинном обучении в 2025 году
• 5 модулей Python для исследования Вселенной
• Как профессионально писать логи Python

Читайте нас в Telegram, VK и Дзен

---

Перевод статьи GeeksforGeeks: Linear Regression (Python Implementation)