Графовые нейронные сети (GNN) представляют собой одну из наиболее интересных и быстро развивающихся архитектур в области глубокого обучения. Будучи моделями глубокого обучения, предназначенными для обработки данных, структурированных в виде графов, GNN обладают универсальностью и огромными обучающими возможностями.
Среди различных типов GNN наиболее распространенной и широко применяемой моделью стали графовые сверточные сети (GCN). Инновационность GCN обусловлена их способностью использовать для прогнозирования как особенности узла, так и его локальность, что обеспечивает эффективный способ обработки данных, структурированных в виде графов.
В этой статье будет подробно описан механизм работы слоя GCN с объяснением его внутреннего устройства. Кроме того, вы узнаете, как практически применять этот слой для решения задач классификации узлов с использованием в качестве инструмента PyTorch Geometric.
PyTorch Geometric (PyG) — это специализированное расширение PyTorch, созданное для разработки и реализации GNN. Эта продвинутая и в то же время удобная в использовании библиотека предоставляет полный набор инструментов для машинного обучения на основе графов. Для начала нашего путешествия потребуется установка PyTorch Geometric. Если вы используете Google Colab, то фреймворк PyTorch уже должен быть установлен. Поэтому все, что нам нужно сделать, — это выполнить несколько дополнительных команд.
Весь код доступен на Google Colab и GitHub.
!pip install torch_geometric
import torch
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
Теперь ознакомимся с набором данных, который будет использован в этом руководстве.
I. Графовые данные
Графы являются важной структурой для представления отношений между объектами. С графовыми данными можно столкнуться во множестве реальных сценариев, таких как социальные и компьютерные сети, химические структуры молекул, обработка естественного языка, распознавание изображений и т. д.
В этой статье будет изучен часто используемый набор данных Карате-клуб Закари.
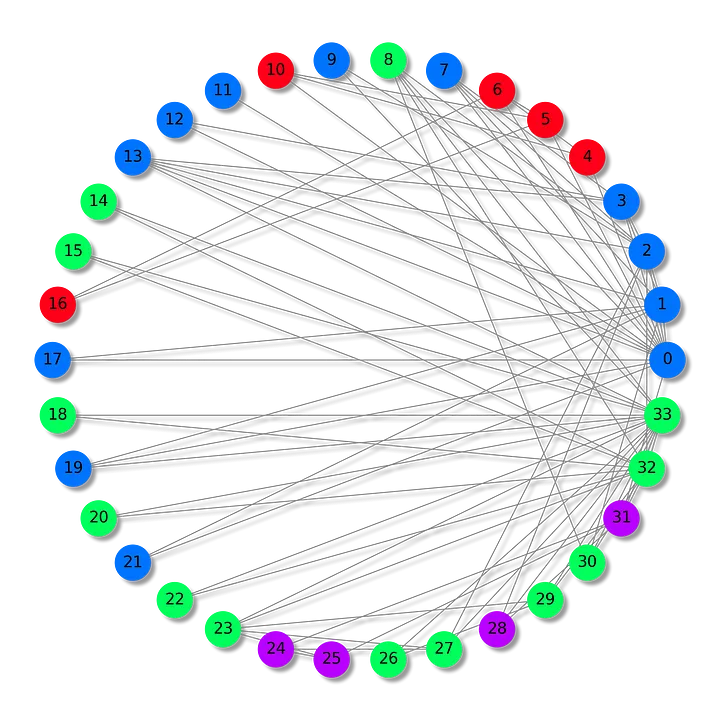
Набор данных “Карате-клуб Закари” отражает взаимоотношения, сложившиеся в одном карате-клубе и изучавшиеся Уэйном В. Закари в 1970-х годах. Это своего рода социальная сеть, в которой каждый узел представляет члена клуба, а ребра между узлами — взаимодействия вне клубной среды.
В данном сценарии члены клуба разделены на четыре группы. Наша задача — безошибочно установить групповую принадлежность каждого из членов клуба (классификация узлов), основываясь на модели их взаимодействия.
Импортируем набор данных с помощью встроенной функции PyG и разберемся с используемым объектом Datasets.
from torch_geometric.datasets import KarateClub
# Import dataset from PyTorch Geometric
dataset = KarateClub()# Информация на вывод
print(dataset)
print('------------')
print(f'Number of graphs: {len(dataset)}')
print(f'Number of features: {dataset.num_features}')
print(f'Number of classes: {dataset.num_classes}')
KarateClub()
------------
Number of graphs: 1
Number of features: 34
Number of classes: 4
В этом наборе данных есть только один граф, в котором каждый узел имеет вектор признаков из 34 измерений и относится к одному из четырех классов (четыре группы). Фактически объект Datasets можно рассматривать как коллекцию объектов Data (графовых).
Дополнительное исследование уникального графа позволит лучше его изучить.
# Вывод первого элемента
print(f'Graph: {dataset[0]}')
Graph: Data(x=[34, 34], edge_index=[2, 156], y=[34], train_mask=[34])
Особенно интересен объект Data. Выведя его, получим полную информационную сводку по исследуемому графу.
x=[34, 34]— матрица признаков узла в форме (количество узлов, количество признаков). В нашем случае это означает, что есть 34 узла (34 члена), каждый узел соотнесен с 34-мерным вектором признаков.edge_index=[2, 156]представляет собой связность графа (как связаны узлы) с формой (2 — количество направленных ребер).y=[34]— истинные метки узлов. В данной задаче каждый узел отнесен к одному классу (группе), поэтому мы имеем одно значение для каждого узла.train_mask=[34]— опциональный атрибут, указывающий, какие узлы следует использовать для обучения с помощью списка утвержденийTrueилиFalse.
Выведем каждый из этих тензоров, чтобы понять, что они хранят. Начнем с признаков узлов.
data = dataset[0]
print(f'x = {data.x.shape}')
print(data.x)
x = torch.Size([34, 34])
tensor([[1., 0., 0., ..., 0., 0., 0.],
[0., 1., 0., ..., 0., 0., 0.],
[0., 0., 1., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 1., 0., 0.],
[0., 0., 0., ..., 0., 1., 0.],
[0., 0., 0., ..., 0., 0., 1.]])
Здесь матрица признаков узла x является матрицей тождества: она не содержит никакой релевантной информации об узлах. Она могла бы содержать такую информацию, как возраст, уровень мастерства и т. д., но в нашем наборе данных это не так. Поэтому нам придется классифицировать узлы, просто глядя на их связи.
Теперь выведем индекс ребра.
print(f'edge_index = {data.edge_index.shape}')
print(data.edge_index)
edge_index = torch.Size([2, 156])
tensor([[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1,
1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3,
3, 3, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7,
7, 7, 8, 8, 8, 8, 8, 9, 9, 10, 10, 10, 11, 12, 12, 13, 13, 13,
13, 13, 14, 14, 15, 15, 16, 16, 17, 17, 18, 18, 19, 19, 19, 20, 20, 21,
21, 22, 22, 23, 23, 23, 23, 23, 24, 24, 24, 25, 25, 25, 26, 26, 27, 27,
27, 27, 28, 28, 28, 29, 29, 29, 29, 30, 30, 30, 30, 31, 31, 31, 31, 31,
31, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 33, 33, 33, 33, 33,
33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33],
[ 1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 17, 19, 21, 31, 0, 2,
3, 7, 13, 17, 19, 21, 30, 0, 1, 3, 7, 8, 9, 13, 27, 28, 32, 0,
1, 2, 7, 12, 13, 0, 6, 10, 0, 6, 10, 16, 0, 4, 5, 16, 0, 1,
2, 3, 0, 2, 30, 32, 33, 2, 33, 0, 4, 5, 0, 0, 3, 0, 1, 2,
3, 33, 32, 33, 32, 33, 5, 6, 0, 1, 32, 33, 0, 1, 33, 32, 33, 0,
1, 32, 33, 25, 27, 29, 32, 33, 25, 27, 31, 23, 24, 31, 29, 33, 2, 23,
24, 33, 2, 31, 33, 23, 26, 32, 33, 1, 8, 32, 33, 0, 24, 25, 28, 32,
33, 2, 8, 14, 15, 18, 20, 22, 23, 29, 30, 31, 33, 8, 9, 13, 14, 15,
18, 19, 20, 22, 23, 26, 27, 28, 29, 30, 31, 32]])
В теории графов и сетевом анализе связь между узлами хранится с помощью различных структур данных. Одной из таких структур данных является edge_index, в которой связи графа хранятся в двух списках (156 направленных ребер, что равно 78 двунаправленным). Причина наличия двух списков заключается в том, что в одном списке хранятся узлы-источники, а во втором — узлы назначения.
Этот метод известен как формат списка координат (COO), который является средством эффективного хранения разреженной матрицы. Разреженные матрицы — это структуры данных, в которых эффективно хранятся матрицы с большинством нулевых элементов. В формате COO хранятся только ненулевые элементы, что позволяет экономить память и вычислительные ресурсы.
Напротив, более интуитивно понятным и простым способом представления связности графа является матрица смежности A. Это квадратная матрица, в которой каждый элемент Aᵢⱼ указывает на наличие или отсутствие в графе ребра от узла i к узлу j. Другими словами, ненулевой элемент Aᵢⱼ означает наличие связи между узлом i и узлом j, а нулевой — отсутствие прямой связи.
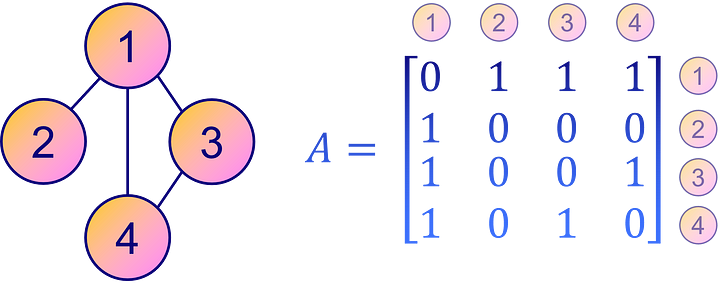
Однако матрица смежности не так компактна, как формат COO для разреженных матриц или графов с меньшим количеством ребер. Тем не менее в плане наглядности и удобства интерпретации матрица смежности остается популярным выбором для представления связности графа.
Матрица смежности может быть выведена из edge_index с помощью функции to_dense_adj().
from torch_geometric.utils import to_dense_adj
A = to_dense_adj(data.edge_index)[0].numpy().astype(int)
print(f'A = {A.shape}')
print(A)
A = (34, 34)
[[0 1 1 ... 1 0 0]
[1 0 1 ... 0 0 0]
[1 1 0 ... 0 1 0]
...
[1 0 0 ... 0 1 1]
[0 0 1 ... 1 0 1]
[0 0 0 ... 1 1 0]]
В графовых данных относительно редко встречаются узлы, плотно связанные между собой. Наша матрица смежности A разрежена (заполнена нулями).
Во многих реальных графах большинство узлов связаны лишь с несколькими другими узлами, что приводит к большому количеству нулей в матрице смежности. Хранение такого количества нулей неэффективно, поэтому в PyG принят формат COO.
Напротив, истинные метки легко понять.
print(f'y = {data.y.shape}')
print(data.y)
y = torch.Size([34])
tensor([1, 1, 1, 1, 3, 3, 3, 1, 0, 1, 3, 1, 1, 1, 0, 0, 3, 1, 0, 1, 0, 1, 0, 0,
2, 2, 0, 0, 2, 0, 0, 2, 0, 0])
Наши метки истинности узлов, хранящиеся в y, просто кодируют номер группы (0, 1, 2, 3) для каждого узла, поэтому мы имеем 34 значения.
Выведем train mask.
print(f'train_mask = {data.train_mask.shape}')
print(data.train_mask)
train_mask = torch.Size([34])
tensor([ True, False, False, False, True, False, False, False, True, False,
False, False, False, False, False, False, False, False, False, False,
False, False, False, False, True, False, False, False, False, False,
False, False, False, False])
Train mask показывает, какие узлы должны использоваться для обучения с утверждениями True. Эти узлы представляют собой обучающее множество, а остальные можно рассматривать как тестовое множество. Такое разделение помогает оценить модель, предоставляя для тестирования данные, с которыми модель никогда не взаимодействовала.
Но мы еще не закончили! Объект Data может предложить еще много интересного. Он предоставляет различные полезные функции, позволяющие исследовать некоторые свойства графа. Например:
is_directed()позволяет определить, является ли граф направленным. Направленный граф означает, что матрица смежности не является симметричной, т. е. направление ребер имеет значение в связях между узлами.isolated_nodes()проверяет, не связаны ли некоторые узлы с остальной частью графа. Такие узлы могут представлять трудности в задачах типа классификации из-за отсутствия связей.has_self_loops()показывает, соединен ли хотя бы один узел с самим собой. Это отличается от концепции петель: петля подразумевает путь, который начинается и заканчивается в одном и том же узле, пересекая другие узлы по пути.
В контексте набора данных “Карате-клуб Закари” все перечисленные свойства возвращают значение False. Это означает, что граф не является направленным, не имеет изолированных узлов и ни один из узлов не соединен сам с собой.
print(f'Edges are directed: {data.is_directed()}')
print(f'Graph has isolated nodes: {data.has_isolated_nodes()}')
print(f'Graph has loops: {data.has_self_loops()}')
Edges are directed: False
Graph has isolated nodes: False
Graph has loops: False
Наконец, можно преобразовать граф из PyTorch Geometric в популярную графовую библиотеку NetworkX с помощью to_networkx. Это особенно удобно при визуализации небольшого графа с использованием networkx и matplotlib.
Построим граф нашего набора данных, используя для каждой группы свой цвет.
from torch_geometric.utils import to_networkx
G = to_networkx(data, to_undirected=True)
plt.figure(figsize=(12,12))
plt.axis('off')
nx.draw_networkx(G,
pos=nx.spring_layout(G, seed=0),
with_labels=True,
node_size=800,
node_color=data.y,
cmap="hsv",
vmin=-2,
vmax=3,
width=0.8,
edge_color="grey",
font_size=14
)
plt.show()
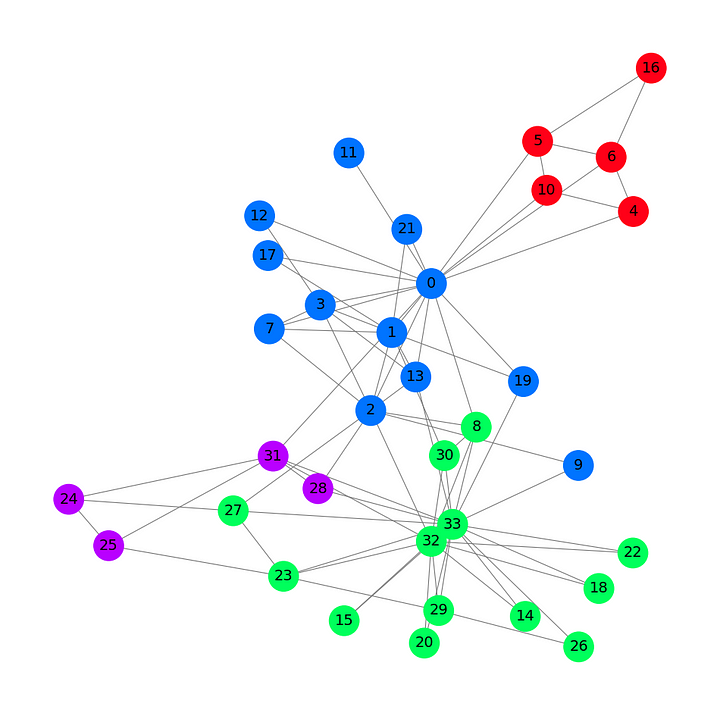
На этом графе, основанном на наборе данных “Карате-клуб Закари”, показаны 34 узла, 78 (двунаправленных) ребер и 4 метки. Также на нем имеются 4 разных цвета. Теперь перейдем к представлению архитектуры графовой сверточной сети.
II. Графовая сверточная сеть
Целью данного раздела является представление и построение с нуля графового сверточного слоя.
В традиционных нейронных сетях линейные слои применяют линейное преобразование к поступающим данным. Такое преобразование трансформирует входные признаки x в скрытые векторы h с помощью весовой матрицы 𝐖. Пренебрегая на время смещениями, это можно выразить следующим образом:
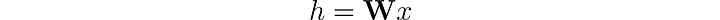
При работе с графовыми данными дополнительный уровень сложности добавляется за счет связей между узлами. Эти связи имеют значение, поскольку в контексте сетей принято считать, что схожие узлы с большей вероятностью будут связаны друг с другом, чем несхожие. Такое явление называется сетевой гомофилией.
Мы можем разнообразить представление узла, объединив его признаки с признаками его соседей. Эта операция называется сверткой или агрегированием соседей. Представим соседство узла i, включая его самого, в виде Ñ.
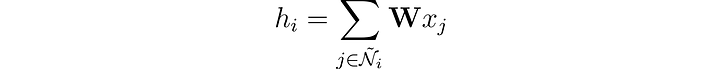
В отличие от фильтров в сверточных нейронных сетях (CNN), весовая матрица 𝐖 уникальна и является общей для каждого узла. Но есть и другая проблема: у узлов нет фиксированного числа соседей, как у пикселей.
Как быть в ситуации, когда у одного узла всего один сосед, а у другого — 500? Если просто просуммировать векторы признаков, то для узла с 500 соседями результирующий эмбеддинг h будет гораздо больше. Чтобы обеспечить одинаковый диапазон значений для всех узлов и их сопоставимость между собой, можно нормировать результат на основе степени узлов, где степень означает количество связей, которыми обладает узел.

Мы почти у цели! Представленный в работе Томаса Кипфа (Thomas N. Kipf) и Макса Веллинга (Max Welling) от 2016 года графовый сверточной слой обладает одним решающим усовершенствованием.
Авторы заметили, что признаки из узлов с многочисленными соседями распространяются гораздо легче, чем из более изолированных узлов. Чтобы нивелировать этот эффект, они предложили присваивать бóльшие веса признакам из узлов с меньшим количеством соседей, тем самым уравнивая влияние на все узлы.
Эта операция записывается в таком виде:
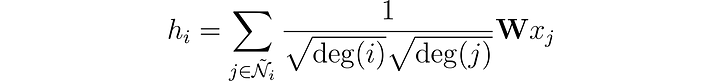
Заметим, что когда i и j имеют одинаковое число соседей, это эквивалентно нашему слою. Теперь посмотрим, как реализовать это на языке Python с помощью PyTorch Geometric.
III. Реализация GCN
PyTorch Geometric предоставляет функцию GCNConv, которая непосредственно реализует графовый сверточный слой.
В этом примере создадим базовую графовую сверточную сеть с одним GCN-слоем, функцией активации ReLU и линейным выходным слоем. Этот выходной слой будет выдавать четыре значения, соответствующие нашим четырем категориям, причем наибольшее значение будет определять класс каждого узла.
В следующем блоке кода определяем GCN-слой с трехмерным скрытым слоем.
from torch.nn import Linear
from torch_geometric.nn import GCNConv
class GCN(torch.nn.Module):
def __init__(self):
super().__init__()
self.gcn = GCNConv(dataset.num_features, 3)
self.out = Linear(3, dataset.num_classes) def forward(self, x, edge_index):
h = self.gcn(x, edge_index).relu()
z = self.out(h)
return h, zmodel = GCN()
print(model)
GCN(
(gcn): GCNConv(34, 3)
(out): Linear(in_features=3, out_features=4, bias=True)
)
Если добавить второй GCN-слой, то наша модель будет агрегировать векторы признаков не только от соседей каждого узла, но и от соседей этих соседей.
Можно создать стек нескольких графовых слоев, чтобы агрегировать все более и более удаленные значения, но есть одна загвоздка: если добавить слишком много слоев, агрегирование станет настолько интенсивным, что все эмбеддинги будут выглядеть одинаково. Это явление называется пересглаживанием и может стать настоящей проблемой, если слоев слишком много.
Теперь, когда мы определили GNN, напишем простой цикл обучения с помощью PyTorch. Я выбрал обычную функцию кросс-энтропии потерь, поскольку это задача мультиклассовой классификации, с Adam в качестве оптимизатора. В данной статье мы не будем реализовывать разделение на обучение/тестирование, чтобы сохранить простоту стиля и сосредоточиться на том, как обучаются GNN.
Цикл обучения стандартен: мы пытаемся предсказать правильные метки и сравниваем результаты GCN со значениями, хранящимися в файле data.y. Погрешность вычисляется по потерям кросс-энтропии и передается в обратном направлении с помощью Adam для точной настройки весов и смещений GNN. Мы выводим метрики каждые 10 эпох.
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.02)
# Расчет точности
def accuracy(pred_y, y):
return (pred_y == y).sum() / len(y)
# Данные для анимаций
embeddings = []
losses = []
accuracies = []
outputs = []
# Обучающий цикл
for epoch in range(201):
# Четкие градиенты
optimizer.zero_grad()
# Передача вперед
h, z = model(data.x, data.edge_index)
# Расчет функции потерь
loss = criterion(z, data.y)
# Расчет точности
acc = accuracy(z.argmax(dim=1), data.y)
# Вычисление градиентов
loss.backward()
# Настройка параметров
optimizer.step()
# Хранение данных для анимаций
embeddings.append(h)
losses.append(loss)
accuracies.append(acc)
outputs.append(z.argmax(dim=1))
# Вывод метрик каждые 10 эпох
if epoch % 10 == 0:
print(f'Epoch {epoch:>3} | Loss: {loss:.2f} | Acc: {acc*100:.2f}%')
Epoch 0 | Loss: 1.40 | Acc: 41.18%
Epoch 10 | Loss: 1.21 | Acc: 47.06%
Epoch 20 | Loss: 1.02 | Acc: 67.65%
Epoch 30 | Loss: 0.80 | Acc: 73.53%
Epoch 40 | Loss: 0.59 | Acc: 73.53%
Epoch 50 | Loss: 0.39 | Acc: 94.12%
Epoch 60 | Loss: 0.23 | Acc: 97.06%
Epoch 70 | Loss: 0.13 | Acc: 100.00%
Epoch 80 | Loss: 0.07 | Acc: 100.00%
Epoch 90 | Loss: 0.05 | Acc: 100.00%
Epoch 100 | Loss: 0.03 | Acc: 100.00%
Epoch 110 | Loss: 0.02 | Acc: 100.00%
Epoch 120 | Loss: 0.02 | Acc: 100.00%
Epoch 130 | Loss: 0.02 | Acc: 100.00%
Epoch 140 | Loss: 0.01 | Acc: 100.00%
Epoch 150 | Loss: 0.01 | Acc: 100.00%
Epoch 160 | Loss: 0.01 | Acc: 100.00%
Epoch 170 | Loss: 0.01 | Acc: 100.00%
Epoch 180 | Loss: 0.01 | Acc: 100.00%
Epoch 190 | Loss: 0.01 | Acc: 100.00%
Epoch 200 | Loss: 0.01 | Acc: 100.00%
Неудивительно, что мы достигли 100% точности на обучающем множестве (полном наборе данных). Это означает, что наша модель научилась правильно относить каждого члена карате-клуба к соответствующей группе.
Путем анимирования графа можно получить наглядную визуализацию и увидеть эволюцию предсказаний GNN в процессе обучения.
%%capture
from IPython.display import HTML
from matplotlib import animation
plt.rcParams["animation.bitrate"] = 3000
def animate(i):
G = to_networkx(data, to_undirected=True)
nx.draw_networkx(G,
pos=nx.spring_layout(G, seed=0),
with_labels=True,
node_size=800,
node_color=outputs[i],
cmap="hsv",
vmin=-2,
vmax=3,
width=0.8,
edge_color="grey",
font_size=14
)
plt.title(f'Epoch {i} | Loss: {losses[i]:.2f} | Acc: {accuracies[i]*100:.2f}%',
fontsize=18, pad=20)fig = plt.figure(figsize=(12, 12))
plt.axis('off')
anim = animation.FuncAnimation(fig, animate, \
np.arange(0, 200, 10), interval=500, repeat=True)
html = HTML(anim.to_html5_video())
display(html)

Первые предсказания носят случайный характер, но через некоторое время GCN идеально маркирует все узлы. Действительно, итоговый график совпадает с тем, который мы построили в конце первого раздела. Но чему же на самом деле учится GCN?
Путем агрегирования признаков, полученных от соседних узлов, GNN обучается векторному представлению (или эмбеддингу) каждого узла сети. В нашей модели последний слой учится использовать эти представления для получения оптимальных классификаций. Однако эмбеддинги — это реальный продукт GNN.
Выведем эмбеддинги, выученные моделью.
# Вывод эмбеддингов
print(f'Final embeddings = {h.shape}')
print(h)
Final embeddings = torch.Size([34, 3])
tensor([[1.9099e+00, 2.3584e+00, 7.4027e-01],
[2.6203e+00, 2.7997e+00, 0.0000e+00],
[2.2567e+00, 2.2962e+00, 6.4663e-01],
[2.0802e+00, 2.8785e+00, 0.0000e+00],
[0.0000e+00, 0.0000e+00, 2.9694e+00],
[0.0000e+00, 0.0000e+00, 3.3817e+00],
[0.0000e+00, 1.5008e-04, 3.4246e+00],
[1.7593e+00, 2.4292e+00, 2.4551e-01],
[1.9757e+00, 6.1032e-01, 1.8986e+00],
[1.7770e+00, 1.9950e+00, 6.7018e-01],
[0.0000e+00, 1.1683e-04, 2.9738e+00],
[1.8988e+00, 2.0512e+00, 2.6225e-01],
[1.7081e+00, 2.3618e+00, 1.9609e-01],
[1.8303e+00, 2.1591e+00, 3.5906e-01],
[2.0755e+00, 2.7468e-01, 1.9804e+00],
[1.9676e+00, 3.7185e-01, 2.0011e+00],
[0.0000e+00, 0.0000e+00, 3.4787e+00],
[1.6945e+00, 2.0350e+00, 1.9789e-01],
[1.9808e+00, 3.2633e-01, 2.1349e+00],
[1.7846e+00, 1.9585e+00, 4.8021e-01],
[2.0420e+00, 2.7512e-01, 1.9810e+00],
[1.7665e+00, 2.1357e+00, 4.0325e-01],
[1.9870e+00, 3.3886e-01, 2.0421e+00],
[2.0614e+00, 5.1042e-01, 2.4872e+00],
...
[2.1778e+00, 4.4730e-01, 2.0077e+00],
[3.8906e-02, 2.3443e+00, 1.9195e+00],
[3.0748e+00, 0.0000e+00, 3.0789e+00],
[3.4316e+00, 1.9716e-01, 2.5231e+00]], grad_fn=<ReluBackward0>)
Как видно, эмбеддинги не обязательно должны иметь ту же размерность, что и векторы признаков. Здесь я решил уменьшить число измерений с 34 (dataset.num_features) до трех, чтобы получить красивую визуализацию в 3D.
Построим граф этих эмбеддингов до начала обучения в эпоху 0.
# Получение первого эмбеддинга в эпоху 0
embed = h.detach().cpu().numpy()
fig = plt.figure(figsize=(12, 12))
ax = fig.add_subplot(projection='3d')
ax.patch.set_alpha(0)
plt.tick_params(left=False,
bottom=False,
labelleft=False,
labelbottom=False)
ax.scatter(embed[:, 0], embed[:, 1], embed[:, 2],
s=200, c=data.y, cmap="hsv", vmin=-2, vmax=3)
plt.show()
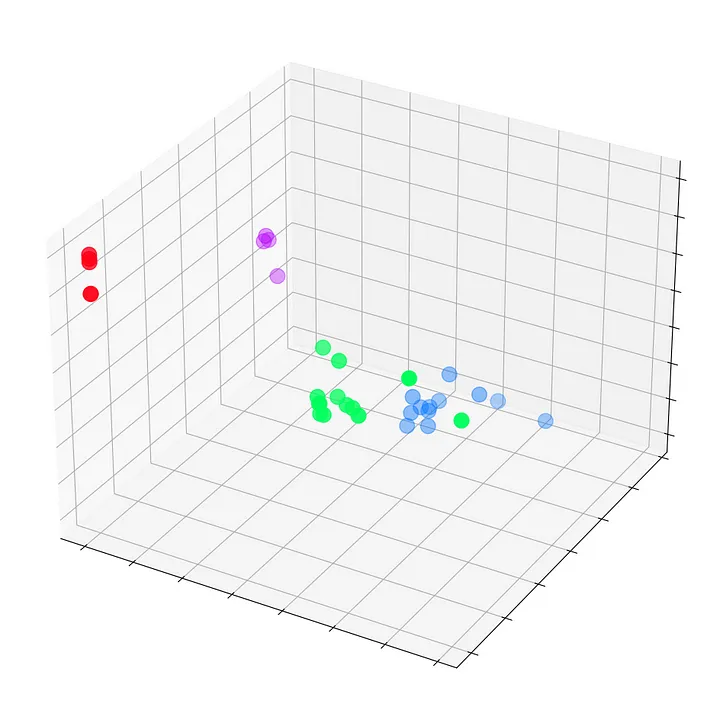
Мы видим все узлы набора данных “Карате-клуб Закари” с их истинными метками (а не предсказаниями модели). На данный момент они разбросаны, поскольку GNN еще не обучена. Но если построить граф этих эмбеддингов на каждом шаге цикла обучения, то можно наглядно увидеть, чему действительно учится GNN.
Посмотрим, как ситуация изменяется со временем, по мере того как GCN все лучше и лучше классифицирует узлы.
%%capture
def animate(i):
embed = embeddings[i].detach().cpu().numpy()
ax.clear()
ax.scatter(embed[:, 0], embed[:, 1], embed[:, 2],
s=200, c=data.y, cmap="hsv", vmin=-2, vmax=3)
plt.title(f'Epoch {i} | Loss: {losses[i]:.2f} | Acc: {accuracies[i]*100:.2f}%',
fontsize=18, pad=40)
fig = plt.figure(figsize=(12, 12))
plt.axis('off')
ax = fig.add_subplot(projection='3d')
plt.tick_params(left=False,
bottom=False,
labelleft=False,
labelbottom=False)
anim = animation.FuncAnimation(fig, animate, \
np.arange(0, 200, 10), interval=800, repeat=True)
html = HTML(anim.to_html5_video())
display(html)
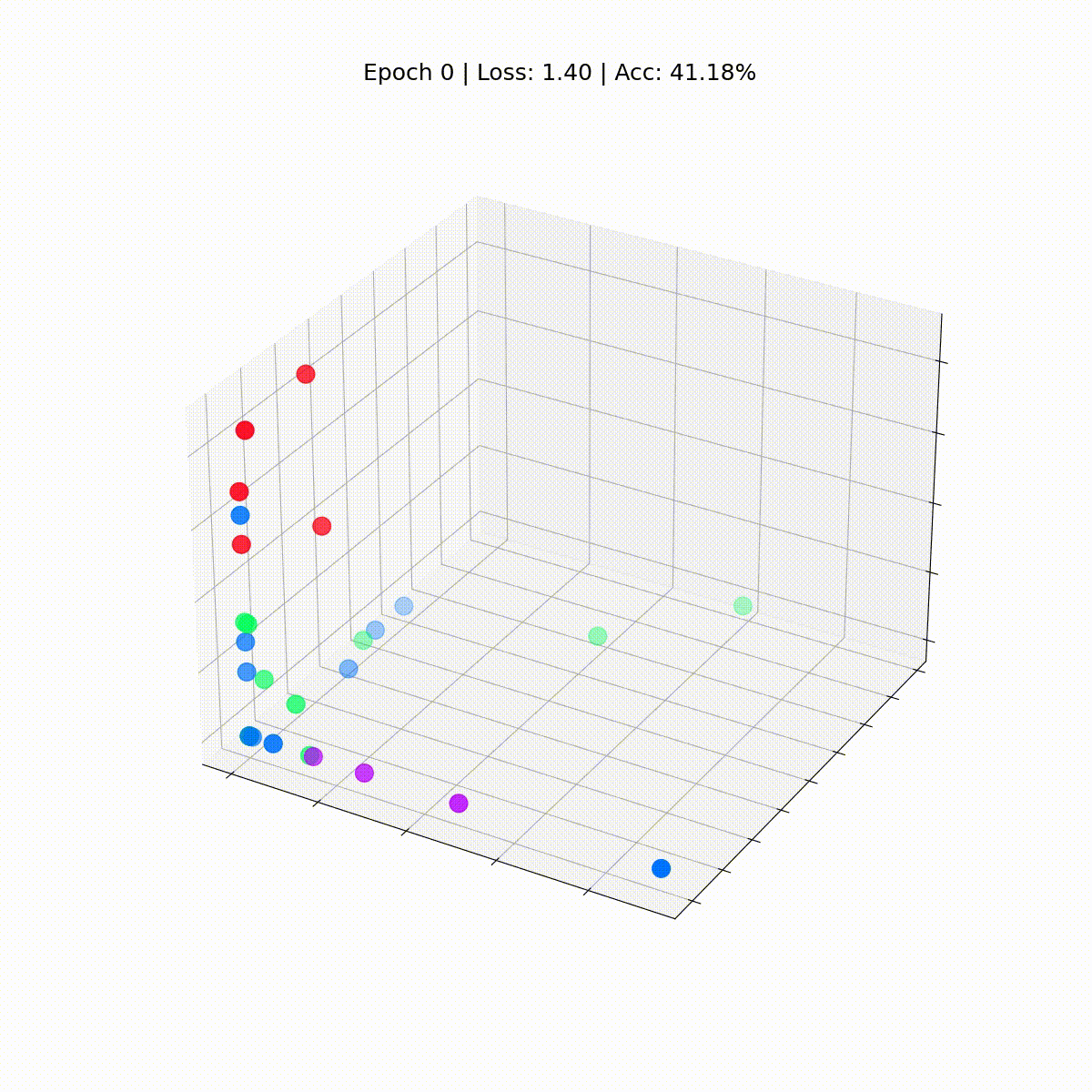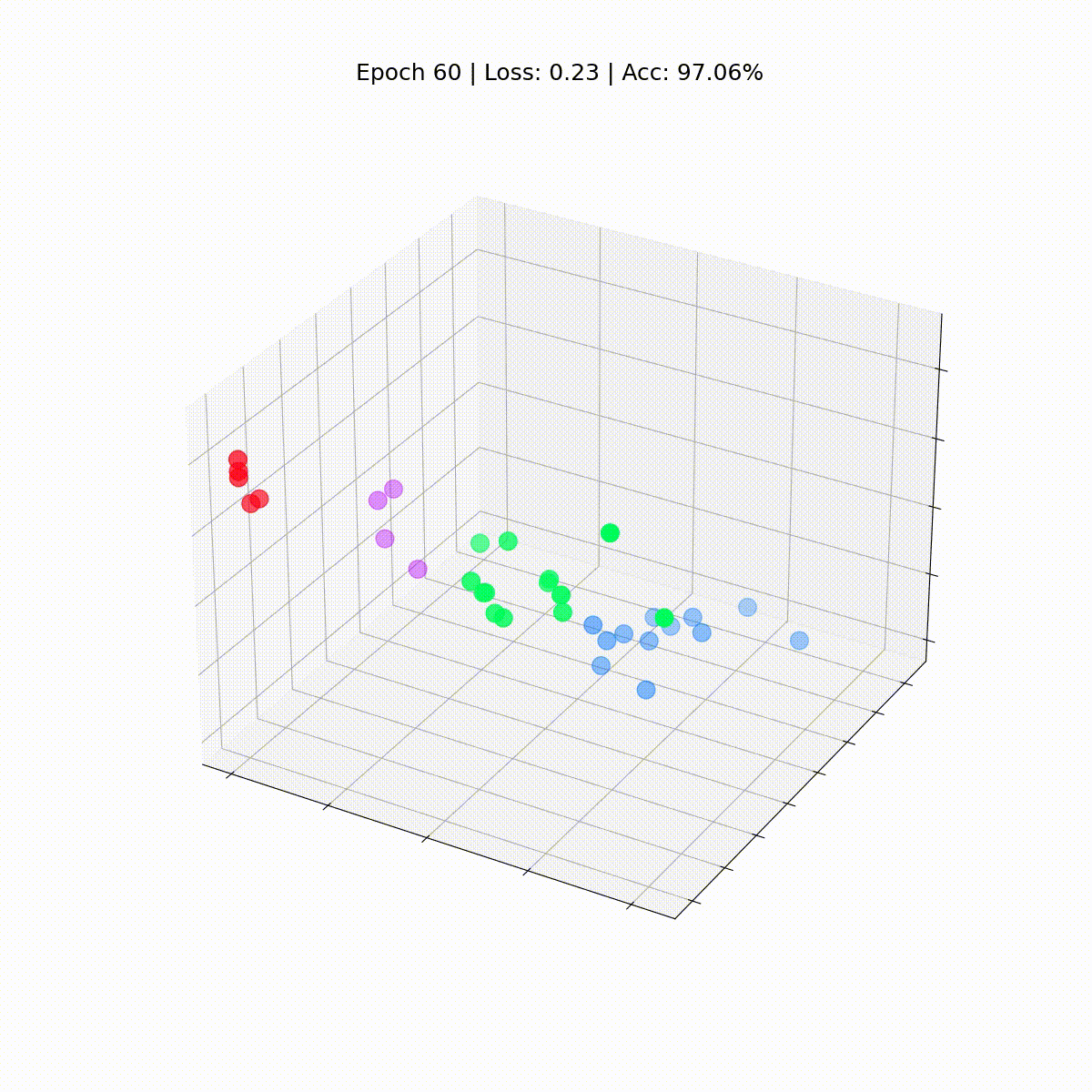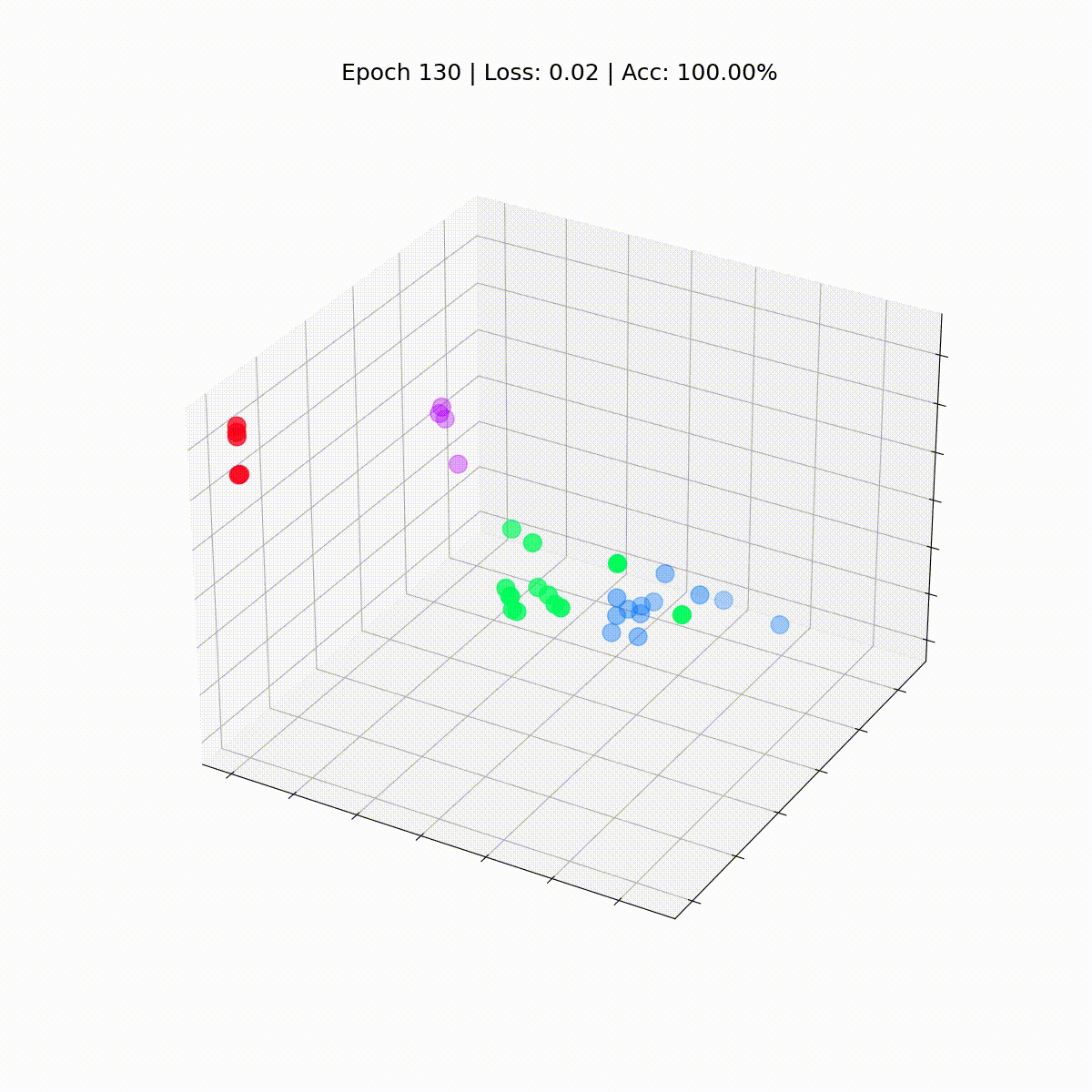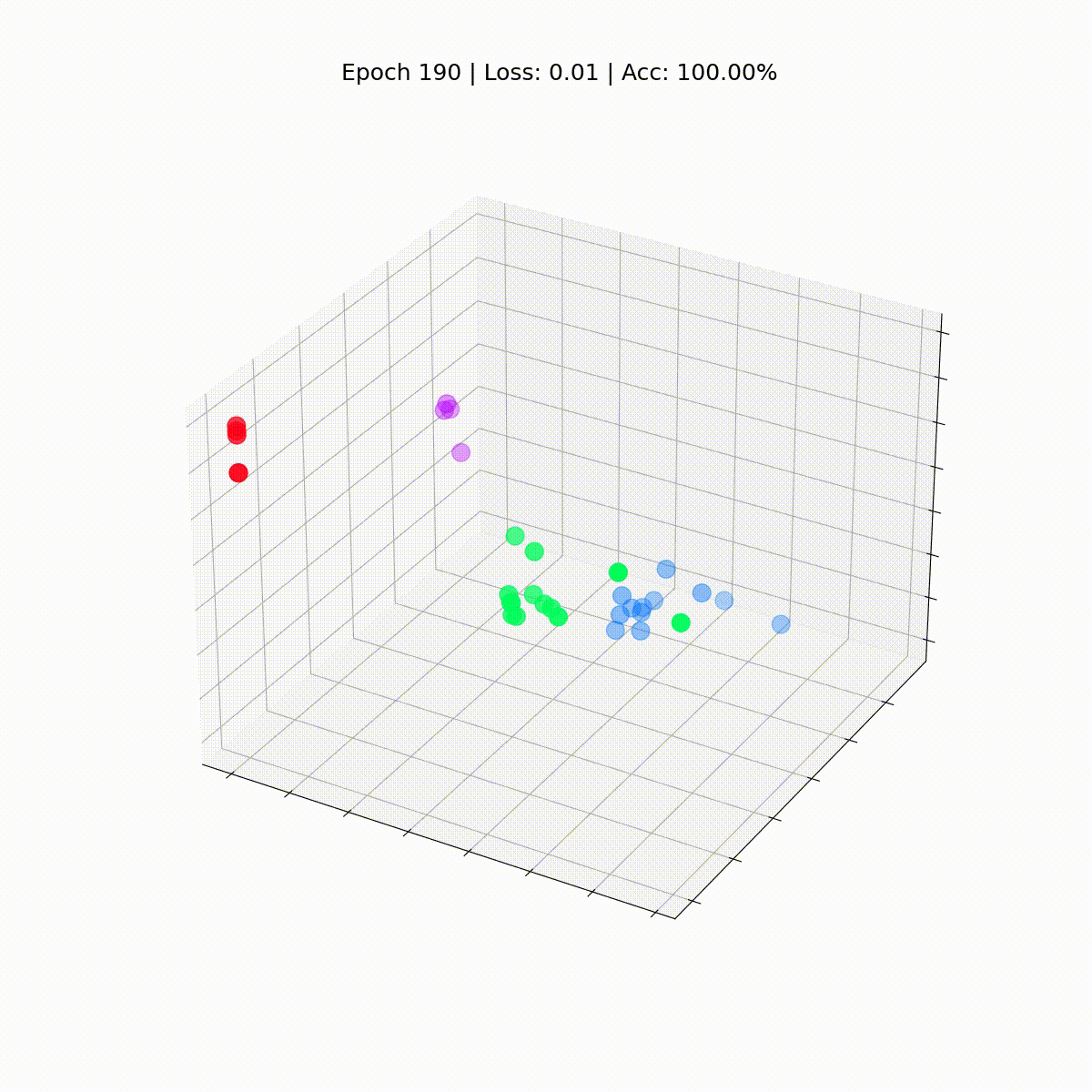
Графовая сверточная сеть эффективно обучается эмбеддингам, которые группируют похожие узлы в отдельные кластеры. Это позволяет конечному линейному слою легко выделять их в отдельные классы.
Эмбеддинги не являются уникальным явлением для GNN: они встречаются повсюду в глубоком обучении. Они также не обязательно должны быть трехмерными: на самом деле они редко бывают таковыми. Например, языковые модели типа BERT создают эмбеддинги с 768 или даже 1024 измерениями.
Дополнительные размерности хранят больше информации об узлах, тексте, изображениях и т. д., но они также создают более крупные модели, которые сложнее обучать. Поэтому выгодно как можно дольше сохранять низкоразмерные эмбеддинги.
Заключение
Графовые сверточные сети — универсальная архитектура, которая может применяться во многих случаях. В этой статье мы познакомились с библиотекой PyTorch Geometric и такими объектами, как Datasets и Data. Затем успешно реконструировали с нуля графовый сверточный слой. После этого применили теорию на практике, реализовав GCN, что позволило нам понять практические аспекты и взаимодействие отдельных компонентов. Наконец, визуализировали процесс обучения и получили четкое представление о том, что требуется от такой сети.
Карате-клуб Закари — это упрощенный набор данных, но он достаточно хорош для понимания наиболее важных концепций в области графовых данных и GNN. Хотя в этой статье речь шла только о классификации узлов, существуют и другие задачи, которые могут решать GNN: предсказание связей (например, для рекомендации друзей), классификация графов (например, для маркировки молекул), генерация графов (например, для создания новых молекул) и т. д.
Читайте также:
- Моделирование логистического роста
- NeuralHash от Apple: принцип работы и слабые места
- Подробное руководство по свёрточным нейронным сетям
Читайте нас в Telegram, VK и Дзен
Перевод статьи Maxime Labonne: Graph Convolutional Networks: Introduction to GNNs






