Что такое дерево? Это структура, основой которой является корень. По мере роста дерева из корня появляется ствол, от которого начинают отходить ветви, а от этих ветвей  —  другие ветви.

Рис.0

На рис. 0 можно увидеть корень как нижнюю часть дерева. Корень вырастает в то, что называется стволом. Из ствола растут ветви, из которых вырастают другие ветви. Кроме того, на дереве есть листья (о них позже).

В программировании дерево выглядит следующим образом:

Рис. 1

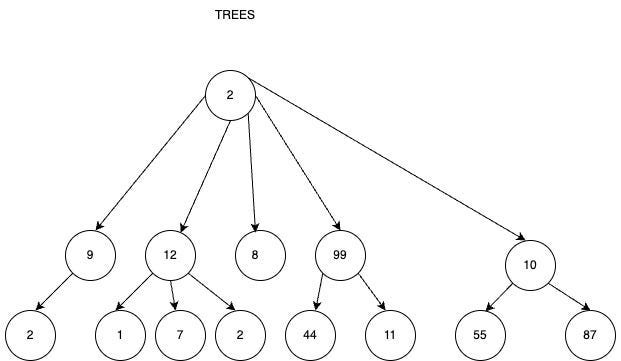
Как видно на рис. 1, корень (2) находится не внизу, как у настоящего дерева, а вверху и растет вниз в отличие от деревьев в реальном мире, которые растут вверх. Когда дерево растет, оно пускает ветви, которые, в свою очередь, пускают еще больше ветвей по мере увеличения размеров дерева.

Рассмотрим особенности структуры двоичных деревьев поиска.

Рис. 2

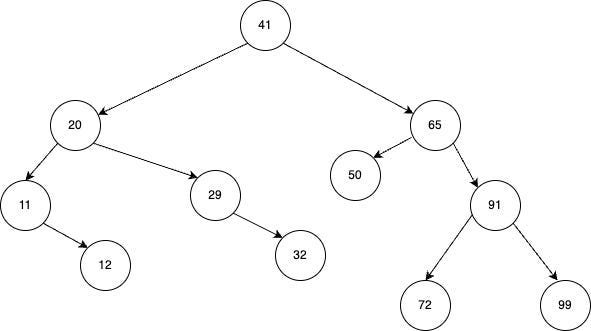
Двоичное дерево поиска (Binary Search Tree, BST) отличается от обычного двоичного дерева тем, что его корень (в данном случае 41) дает начало только двум ветвям (20, 65) и по мере роста дерева у ветвей не может быть больше двух ответвлений.

Теперь определим структуру двоичного дерева поиска на языке программирования.

Корень  —  это верхний узел дерева, а две ветви, которые из него вырастают,  —  это дети (потомки, дочерние ветви).

Рис. 3

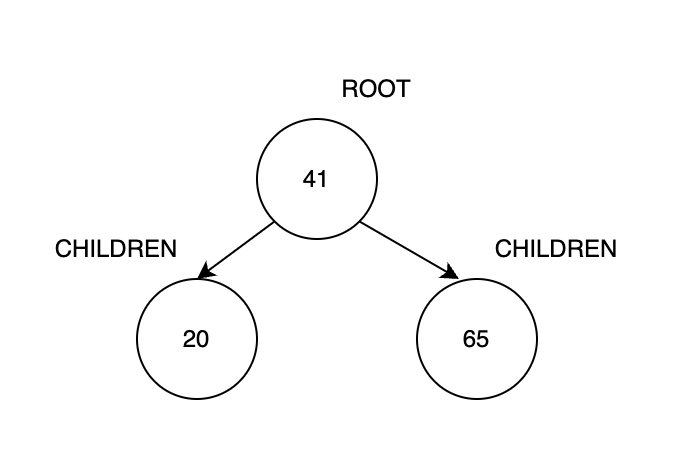
Когда эти дети вырастают, они сами становятся родителями двух детей  —  ветвей, которые из них вырастают (рис. 4). При этом у каждого родителя не может быть больше двух детей.

Рис. 4

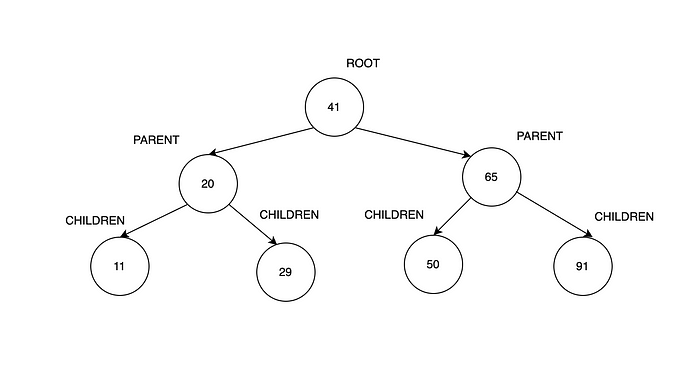
А если родитель не хочет иметь детей? Такое явление в программировании получило название “лист”. Вернемся к изображению настоящего дерева на рис. 0. Когда его ветви переставали расти, на них появлялись листья, что говорило о том, что оттуда ветви уже не вырастут. Но в BST мы не включаем лист, а удаляем соединитель, чтобы показать, что родитель не соединяется ни с одной ветвью, как на рис. 4, где у детей нет соединений со следующей ветвью.

Следует также обратить внимание на то, что ветви BST, растущие от корня, как показано на рис. 4, делятся на левую и правую (относительно корня), а по мере роста дерева  —  на родительские и дочерние ветви.

Если вы внимательно посмотрите на рис. 4, то заметите следующую закономерность: левая родительская ветвь  —  это число меньше корня, а правая родительская ветвь  —  число больше корня. По мере роста дерева у родителей появятся по две дочерние ветви, причем ребенок каждой левой ветви  —  это число меньше родителя, а ребенок каждой правой ветви  —  число больше родителя.

Таким образом, BST используется для упорядочивания элементов или, скажем, чисел в структуре данных.

Что, если нужно добавить ветви в дереве? На языке программирования этот вопрос будет звучать так: как вставить узлы в дерево?

Для этого понадобится определить класс node с конструктором, который будет иметь передаваемое значение параметра. Класс node будет обладать двумя свойствами  —  left и right  —  для обозначения левой и правой позиции ветви. Эти свойства будут установлены в null, поскольку предполагается, что ветвь еще не растет.

Рис. 5

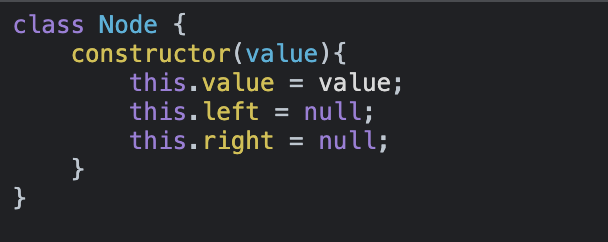
Кроме того, нужно определить класс BST, который будет иметь конструктор. Внутри конструктора будет свойство root, чтобы отслеживать первое значение, вставляемое в дерево. Оно будет установлено в null, поскольку дерево только создается и на данный момент еще пустое. За пределами конструктора будет свойство insert, которое принимает значение параметра, используемого для создания дерева.

Рис. 6

Чтобы добавить новые значения, которые понадобятся для создания дерева, нужно определить класс BST, используя ключевое слово new, которое будет храниться в переменной bst. Затем необходимо вызвать метод insert в классе BST, используя свойство dot в отношении переменной bst.

Рис. 7

Теперь рассмотрим функциональность insert.

Подобно тому, как ранее был определен класс BST, делаем то же самое с Node, который представляет ветвь, создаваемую для свойств, как показано на рис. 5. Затем передаем значение параметра в методе insert в Node, чтобы создать узел дерева.

Рис. 8

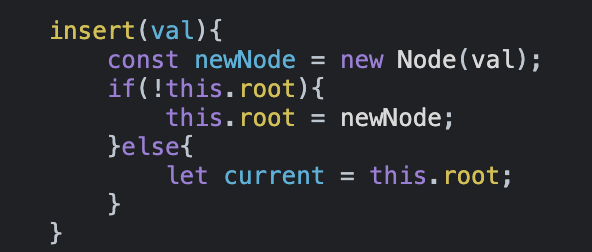
Необходимо проверить, есть ли у дерева корень. Согласно рис. 6, ранее свойство root было установлено нами в null. В этом случае нужно установить корнем созданный нами узел (рис. 8), чтобы дерево имело корень, поскольку без корня не может быть дерева.

Рис. 9

А что, если корень уже создан, и нужно добавить в дерево еще один узел, который будет ветвью? Напомню, что на рис. 4 числа слева были меньше корня, а числа справа больше корня. Это нужно учитывать при добавлении узлов в дерево.

Создадим переменную current, которая будет содержать root и использоваться для отслеживания узлов при добавлении чисел в дерево.

Рис. 10

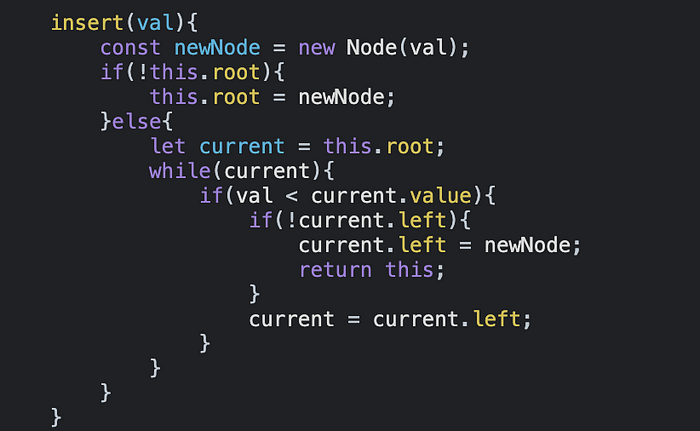
Для вставки в дерево потребуется использовать цикл, который позволит постоянно добавлять столько чисел, сколько нужно. Этот цикл будет применяться для обновления узла current, который вставляется в дерево, имеющее корень по умолчанию, о чем было упомянуто ранее. По мере роста дерева нужно будет обновлять current.

Нам потребуется оператор if, который будет использоваться для сравнения значений, добавляемых в дерево, со значением current, обновляемым циклом while после каждой проверки. Нужно также проверить, есть ли в нашем узле свойство left, поскольку, определяя этот узел, мы установили свойства left и right в null, так как предполагали, что при определении класса node не было дерева.

Мы будем использовать current = current.left как базовый случай для цикла while. Если свойство left узла current равно null, новое значение не вставляется, цикл завершается, так как он вернет false во время следующей итерации.

Рис. 11

Со свойством right поступаем точно так же, как с left.

Рис. 12

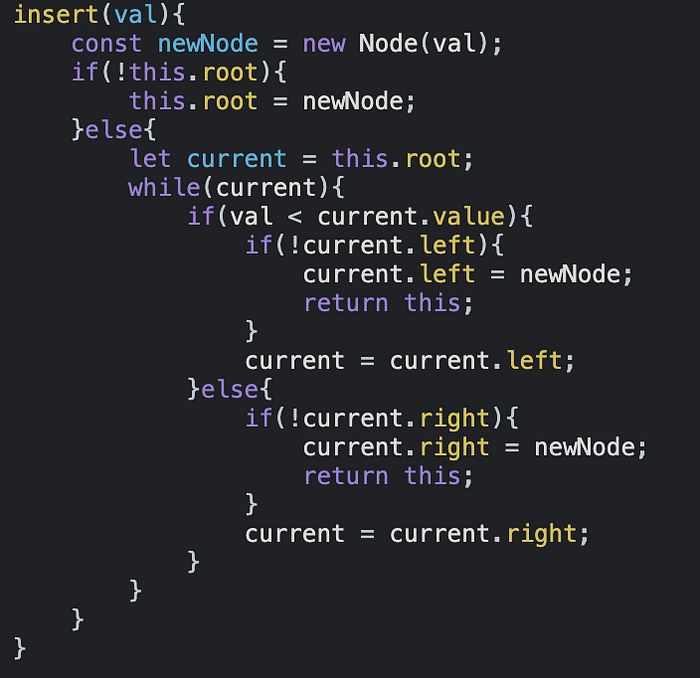
Базовый случай, добавленный нами, оказался верным. Но что, если появятся дублирующиеся числа? Это вызовет проблемы. Поскольку у нас нет средства для проверки этого, можно использовать подсчет или просто пренебречь дублирующимися переменными, добавив оператор if для проверки переменной перед вставкой путем сравнения со значением current.

Рис. 13

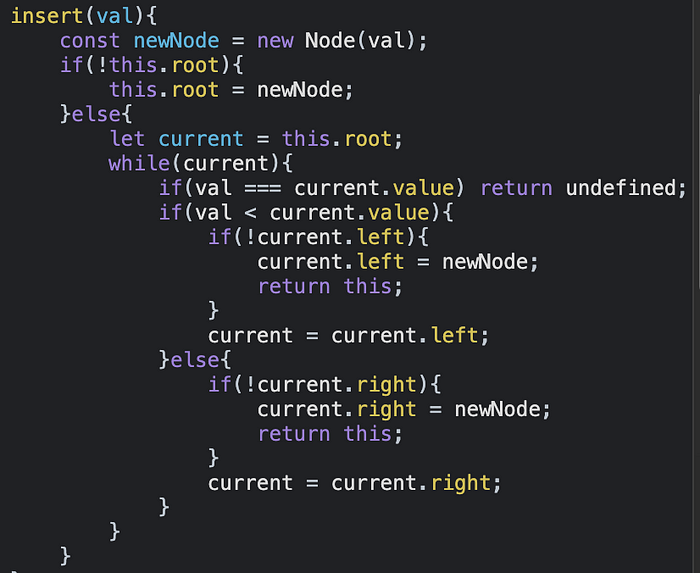
Теперь изучим функциональность find.

Для нахождения узла в дереве используется метод find. Вызывать метод find нужно в классе BST, применяя свойство dot к переменной (см. рис. 7) и передавая переменную, которую нужно найти в дереве, в метод find.

В методе find внутри класса BST сначала проверим, есть ли корень в дереве, так как дерево без корня означает отсутствие ветвей.

Рис. 14

Затем, как мы уже делали ранее, сохраним корень в созданной нами переменной под названием current. Эта переменная будет хранить узел current в дереве, поскольку понадобится использовать цикл для перемещения по всему дереву.

Во время цикла по узлу current необходимо проверить, равно ли значение current значению, передаваемому в метод find. Если да, то мы должны вернуть current.

Рис. 15

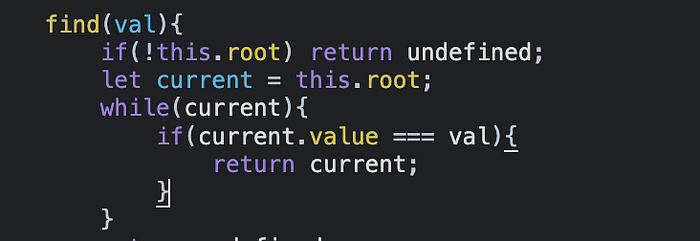
Если нет, то, как и при вставке узлов в дерево, нужно проверить, является ли значение, переданное в метод find, меньше или больше значения current. Если да, то надо обновить значение current так, чтобы при проверке возвращалось значение current.

Рис. 16

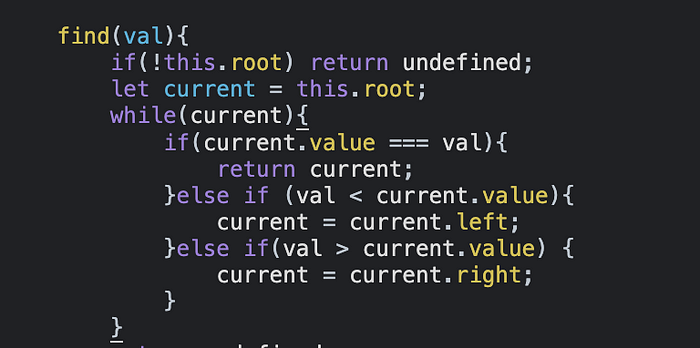
Если после выполнения поиска значение не найдено, цикл while завершается и возвращается undefined.

Рис. 17

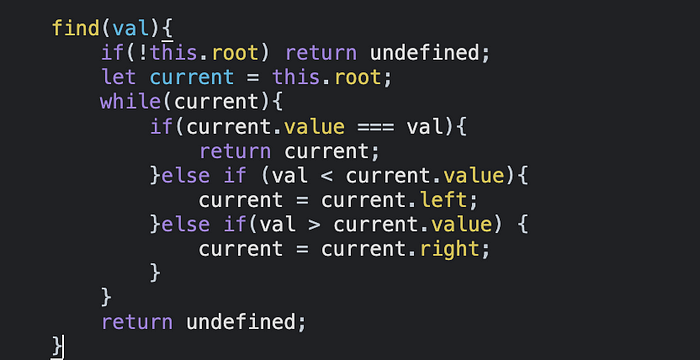
Итак, вот полный код всего алгоритма BST:

class Node {
    constructor(value){
        this.value = value;
        this.left = null;
        this.right = null;
    }
}

class BST {
    constructor(){
        this.root = null;
    }

    insert(val){
        const newNode = new Node(val);
        if(!this.root){
            this.root = newNode;
        }else{
            let current = this.root;
            while(current){
                if(val === current.value) return undefined;
                if(val < current.value){
                    if(!current.left){
                        current.left = newNode;
                        return this;
                    }
                    current = current.left;
                }else{
                    if(!current.right){
                        current.right = newNode;
                        return this;
                    }
                    current = current.right;
                }
            }
        }
    }

    find(val){
        if(!this.root) return undefined;
        let current = this.root;
        while(current){
            if(current.value === val){
                return current;
            }else if (val < current.value){
                current = current.left;
            }else if(val > current.value) {
                current = current.right;
            }
        }
        return undefined;
    }
}

const bst = new BST();

bst.insert(10);
bst.insert(5);
bst.insert(2);
bst.insert(12);
bst.insert(6);
bst.insert(7);

bst.find(10);

Нотация BIG O для BST

  • Для вставки  —  O(logN);
  • для поиска  —  O(logN).

Это не гарантировано. Допустим, у нас одна ветвь по всему дереву вместо двух, поскольку мы знаем, что BST может иметь одну ветвь. Если ограничение на количество ветвей у родителя  —  две, то наличие одной ветви не нарушает это правило.

Рис. 18

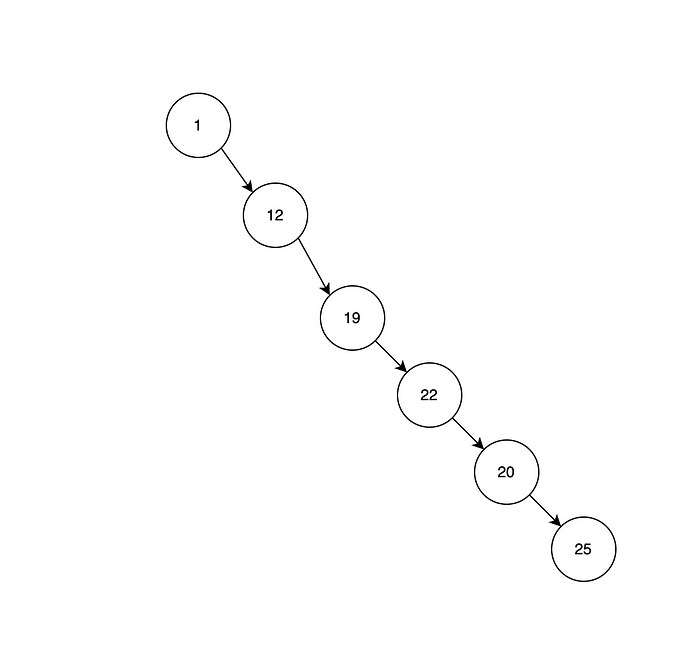
При выполнении поиска, как показано на рис. 18, когда мы движемся вниз, чтобы найти значение 20, прохождение цикла происходит пять раз. А если будет миллион ветвей, которые нужно будет циклически пройти? Вот почему стоит разбить на две ветви, что уменьшит количество циклов при переборе множества ветвей в дереве.

Рис. 19

Заключение

Области применения BST:

  • DOM;
  • сетевая маршрутизация;
  • абстрактные синтаксические деревья;
  • искусственный интеллект, например игра MinMax, подобная TicTacToe;
  • папки в операционных системах;
  • компьютерные файловые системы.

Читайте также:

Читайте нас в Telegram, VK и Дзен

Перевод статьи CalyWorld: Binary Trees and Binary Search Trees

Предыдущая статьяBabyAGI  —  автономный ИИ-агент для оптимизации задач
Следующая статьяPython 4.0: программирование следующего поколения